Cumulative distribution function

P Compute the cumulative distribution function for multiple distributions

Usage

P(
  q,
  dist = "normal",
  lower.tail = TRUE,
  rounding = 5,
  porcentage = FALSE,
  gui = "plot",
  main = NULL,
  ...
)

Arguments

q: quantile. The q argument can have length 1 or 2. See Details.
dist: distribution to use. The default is 'normal'. Options: 'normal', 't-student', 'gumbel', 'binomial', 'poisson', and ....
lower.tail: logical; if TRUE (default), probabilities are $P[X \leq x]$ otherwise, $P[X > x]$. This argument is valid only if q has length 1.
rounding: numerical; it represents the number of decimals for calculating the probability.
porcentage: logical; if FALSE (default), the result in decimal. Otherwise, probability is given in percentage.
gui: default is 'plot'; it graphically displays the result of the probability. Others options are: 'none', 'rstudio' or 'tcltk'.
main: defalt is NULL; it represents title of plot.
...: additional arguments according to the chosen distribution.

Value

P returns the probability and its graphical representation. The result can be given as a percentage or not.

Details

The argument that can have length 2, when we use the functions that give us the probability regions, given by: %<X<%, %<=X<%, %<X<=%, %<=X<=%, %>X>%, %>X=>%, %>X=>% and %>=X=>%. The additional arguments represent the parameters of the distributions, that is:

If dist = "normal" (Default); the additional arguments are: mean ($\mu$) and sd ($\sigma$). The PDF is given by: $$\displaystyle{\frac {1}{\sqrt {2\pi \sigma ^{2}}}}e^{-{\frac {(x-\mu )^{2}}{2\sigma ^{2}}}}, \quad \mu \in \mathbb{R},~\sigma^2 > 0;$$
If dist = "t-student"; the additional argument is: df ($\nu$). The PDF is given by: $$\displaystyle{\frac {\Gamma \left({\frac {\ \nu +1\ }{2}}\right)}{{\sqrt {\pi \ \nu \ }}\ \Gamma \left({\frac {\nu }{\ 2\ }}\right)}}\left(\ 1+{\frac {~x^{2}\ }{\nu }}\ \right)^{-{\frac {\ \nu +1\ }{2}}}, \quad \nu > 1;$$
If dist = "chisq"; the additional argument is: df ($\nu$). The PDF is given by: $$\displaystyle{\frac {1}{2^{k/2}\Gamma (k/2)}}\;x^{k/2-1}e^{-x/2}, \quad \nu > 0;$$

Examples

# Loading package
library(leem)
# Example 1 - Student's t distribution
if (FALSE) { # \dontrun{
P(q = 2, dist = "t-student", df = 10)
P(q = 2, dist = "t-student", df = 10, gui = 'rstudio')
P(q = 2, dist = "t-student", df = 10, gui = 'tcltk')
P(-1 %<X<% 1, dist = "t-student", df = 10)
} # }
# Example 2 - Normal distribution
P(-2,  dist = "normal", mean = 3, sd = 2,
  main = expression(f(x) == (1 / sqrt(n * sigma^2)) *
  exp(-1/2 * (x - mu)^2/sigma^2)))

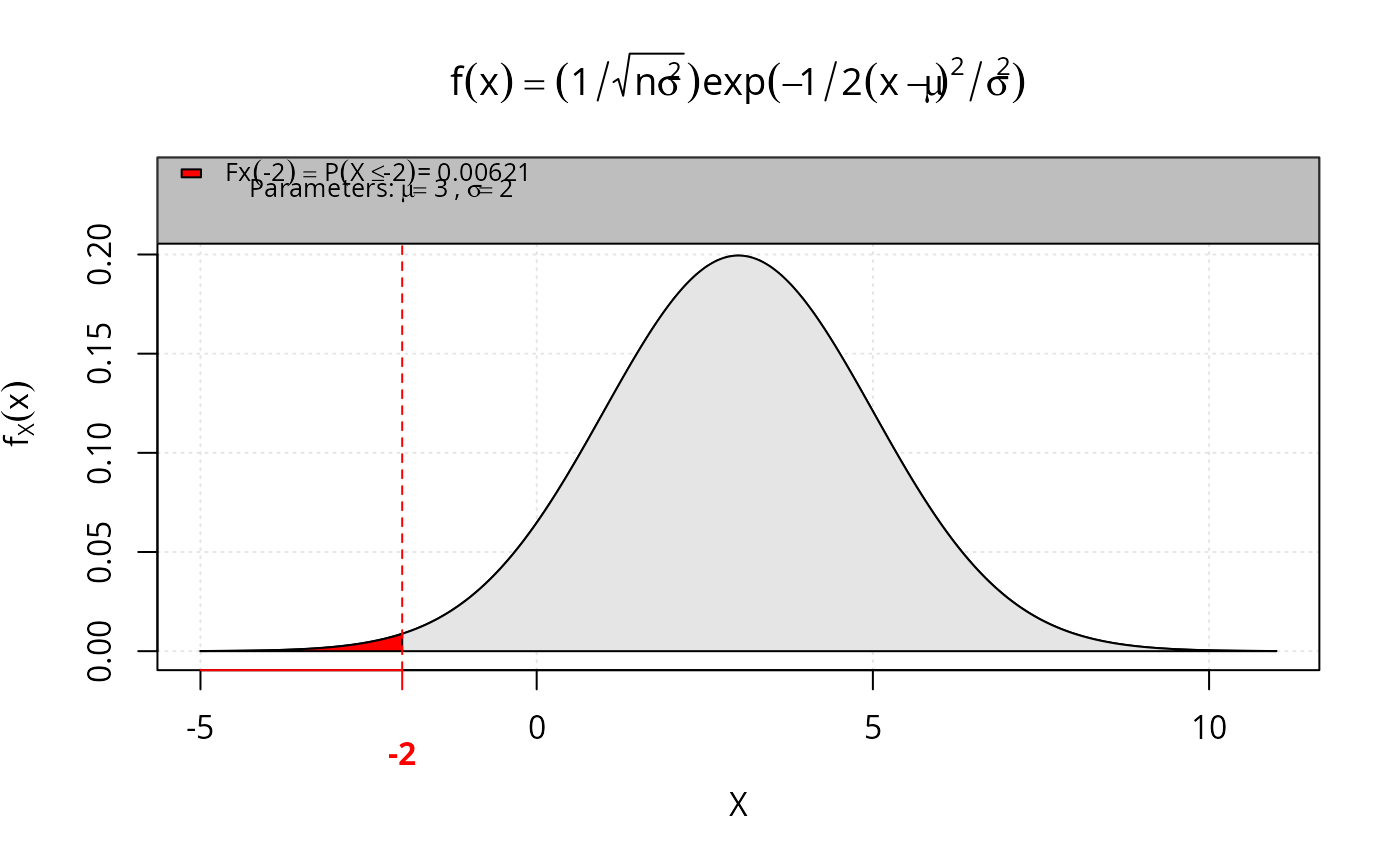#> [1] 0.00621