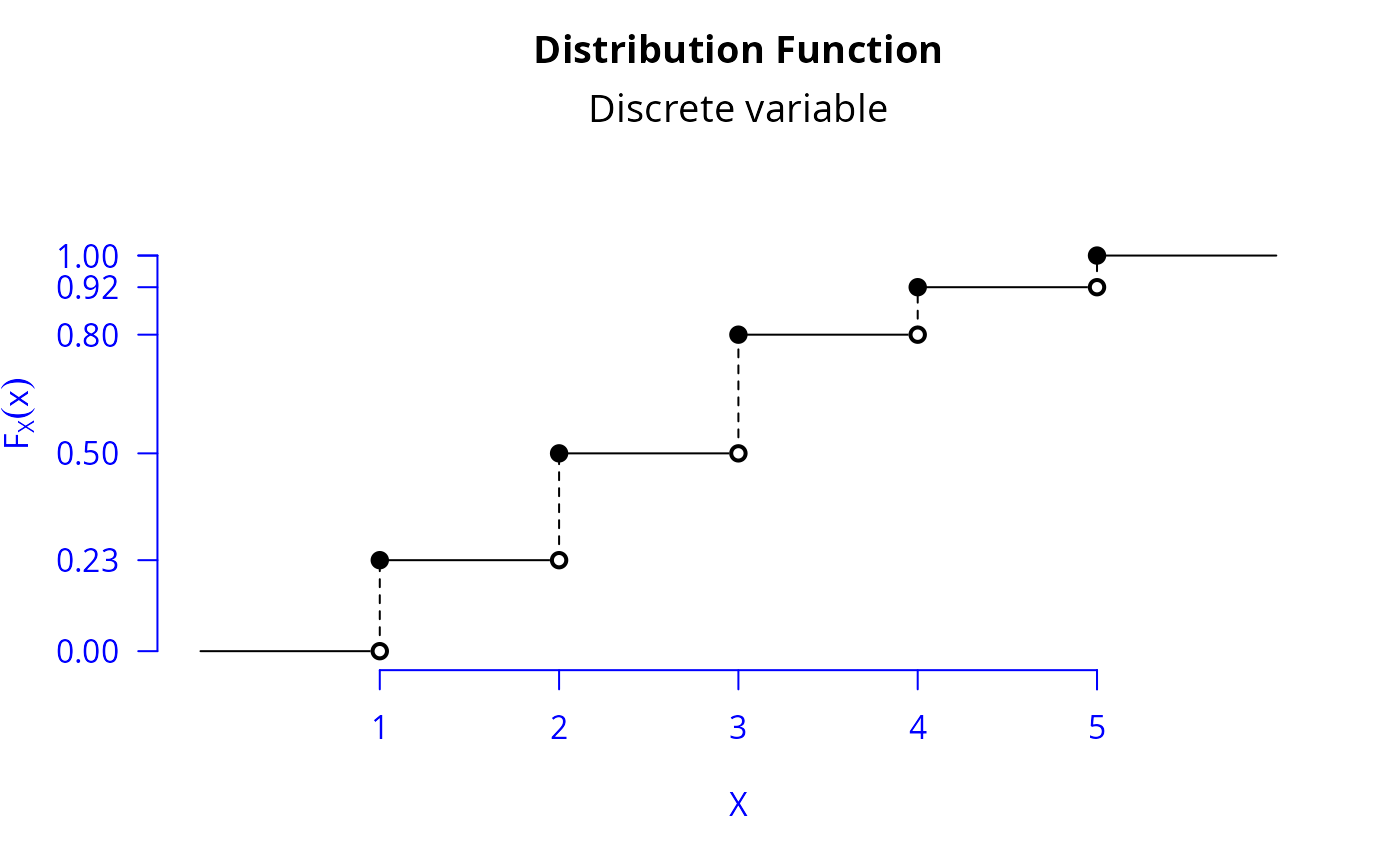
Plot of cumulative distribution function of any discrete variable

Help in building the plot of the cumulative distribution function of any discrete variable

Usage

cdfd(x, fda, main = NULL, xlab = NULL, ylab = NULL)

Arguments

x

numeric vector of values of \(X\). See Details.

fda

numeric vector of \(F_X(x)\). See Details.

main

main title for the plot.

xlab

a label for the x axis.

ylab

a label for the y axis.

Value

The output is plot of distribution function. See Example 1.

Details

Consider the \(X\) distribution:

\(p_X(x)\):	0.23	0.27	0.30	0.12	0.08
\(x\):	1	2	3	4	5

where \(p_X(x)\) and \(x\) are probability function and values of \(X\). Consider also the \(X\) distribution function:

$$ F_X(x) = \left\{\begin{array}{ll} 0, & \textrm{if } x < 1;\\ 0.23, & \textrm{if } 1 \leq x < 2;\\ 0.50, & \textrm{if } 2 \leq x < 3;\\ 0.80, & \textrm{if } 3 \leq x < 4;\\ 0.92, & \textrm{if } 4 \leq x < 5;\\ 1.00 & \textrm{if } x \geq 5.\\ \end{array}\right. $$

This way, the cdfd function needs to consider only the vectors x <- 1:5 and fda <- c(0.23, 0.50, 0.80, 0.92, 1), that is, only the equality conditions for \(x\). See Example 1.

Examples

# Example 1
x <- 1:5
fda <- c(0.23, 0.5, 0.8, 0.92, 1)
cdfd(x, fda)