Estatística e Probabilidade

Aula 05 - Medidas de posição

Ben Dêivide | UFSJ

Filosofia de publicação (Selo DC)

Livro de Apoio

Usaremos Batista (2023):

Ideia sobre medidas de posição

Vamos usar o leem!

library(leem)
showpar()

Tipos de medidas de posição

  • Média aritmética
  • Mediana
  • Moda

Funções leem



Função Finalidade
mean() Média
median() Mediana
mfreq() Moda

Média Aritmética

Definição (Média aritmética): Seja uma amostra \(X_1\), \(X_2\), \(\ldots\), \(X_n\), de uma população \(X_1\), \(X_2\), \(\ldots\), \(X_N\), de tamanhos \(n\) e \(N\), respectivamente, definimos a média aritmética por:

\[\begin{align*} \mu & = \frac{\displaystyle\sum_{i=1}^{N}X_i}{N}, \quad \textrm{(População)} \end{align*}\] e \[\begin{align*} \bar{X} = \frac{\displaystyle\sum_{i=1}^{n}X_i}{n}. \quad \textrm{(Amostra)} \end{align*}\]

Média Aritmética (Dados agrupados)

Definição (Média aritmética): Seja uma amostra \(X_1\), \(X_2\), \(\ldots\), \(X_n\), de tamanho \(n\), agrupados em \(k\) grupos com variáveis \(X_i\) e frequência \(F_i\), ou \(k\) classes com pontos médios \(\tilde{X}_i\) e \(F_i\) frequências, para \(i\) \(=\) \(1\), \(2\), \(\ldots\), \(k\) e \(\sum_{i = 1}^{k}F_i = n\), então a média aritmética de uma amostra, é definida por: \[\begin{align}\label{eq:mediaagrup} \bar{X} & = \left\{\begin{array}{ll} \frac{\sum_{i = 1}^{k}X_i \times F_i}{\sum_{i = 1}^{k}F_i}, & \textrm{agrupados sem intervalo de classe}, \\ &\\ \frac{\sum_{i = 1}^{k}\tilde{X}_i \times F_i}{\sum_{i = 1}^{k}F_i}, & \textrm{agrupados com intervalo de classe},\\ \end{array}\right. \end{align}\] sendo \(\tilde{X}_{i}\) o ponto médio das classes.

Exemplo 1 - Número de erros

Dados do número de erros encontrados em 20 conjuntos de caracteres monitorado em um canal de comunicação.

3 1 0 1 3 2 4 1 3 1
1 1 2 3 3 2 0 2 0 1

\[\begin{align*} \bar{X} = \frac{3 + 1 + \ldots + 1}{20}=\frac{34}{20}= 1,7~\textrm{erros}. \end{align*}\]

Exemplo 1 - Número de erros

Retornando o exemplo anterior…

\[\begin{align*} \bar{X} & = \sum_{i=1}^{n}\tilde{X}_if_i / \sum_{i=1}^{n}f_i \\ & = \frac{0 \times 3 + \ldots + 5 \times 4}{20}\\ & = 1,7~\textrm{erros}. \end{align*}\]


Table of frequency 
Type of variable: discrete

  Groups Fi   Fr Fac1 Fac2 Fp Fac1p Fac2p
1      0  3 0.15    3   20 15    15   100
2      1  7 0.35   10   17 35    50    85
3      2  4 0.20   14   10 20    70    50
4      3  5 0.25   19    6 25    95    30
5      4  1 0.05   20    1  5   100     5
============================================== 
Groups: Discretized grouping 
Fi: Absolute frequency 
Fr: Relative frequency 
Fac1: Cumulative frequency (below) 
Fac2: Cumulative frequency (above) 
Fp: Percentage frequency 
Fac1p: Cumulative percentage frequency (below) 
Fac2p: Cumulative percentage frequency (above)

Exemplo 2 - Challenger

Os dados representam a temperatura (°F) do anel de vedação de cada teste de acionamento ou lançamento real do motor do foguete Challenger

84 40 45 69 68 72 57 78 53 61 76 76
49 83 66 80 60 73 63 52 67 70 79 58
61 67 70 58 67 70 70 67 75 81 75 31

Exemplo (continuação…)

Retornando o exemplo anterior…

\[\begin{align*} \bar{X} & = \sum_{i=1}^{n}X_if_i / n \\ & = \frac{84 + 40 + \ldots + 31}{36}\\ & = 65,86~\textrm{°F}. \end{align*}\]


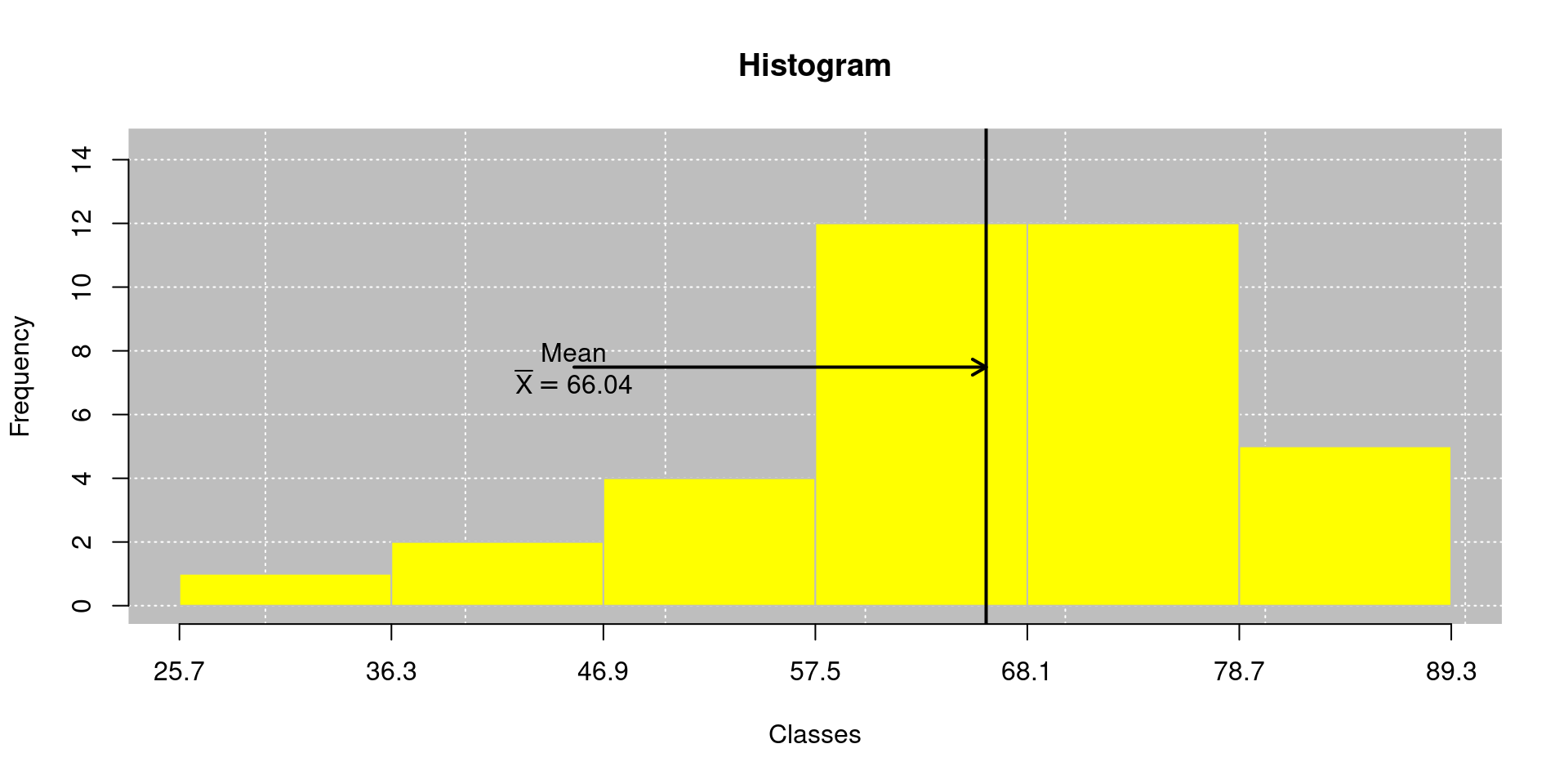
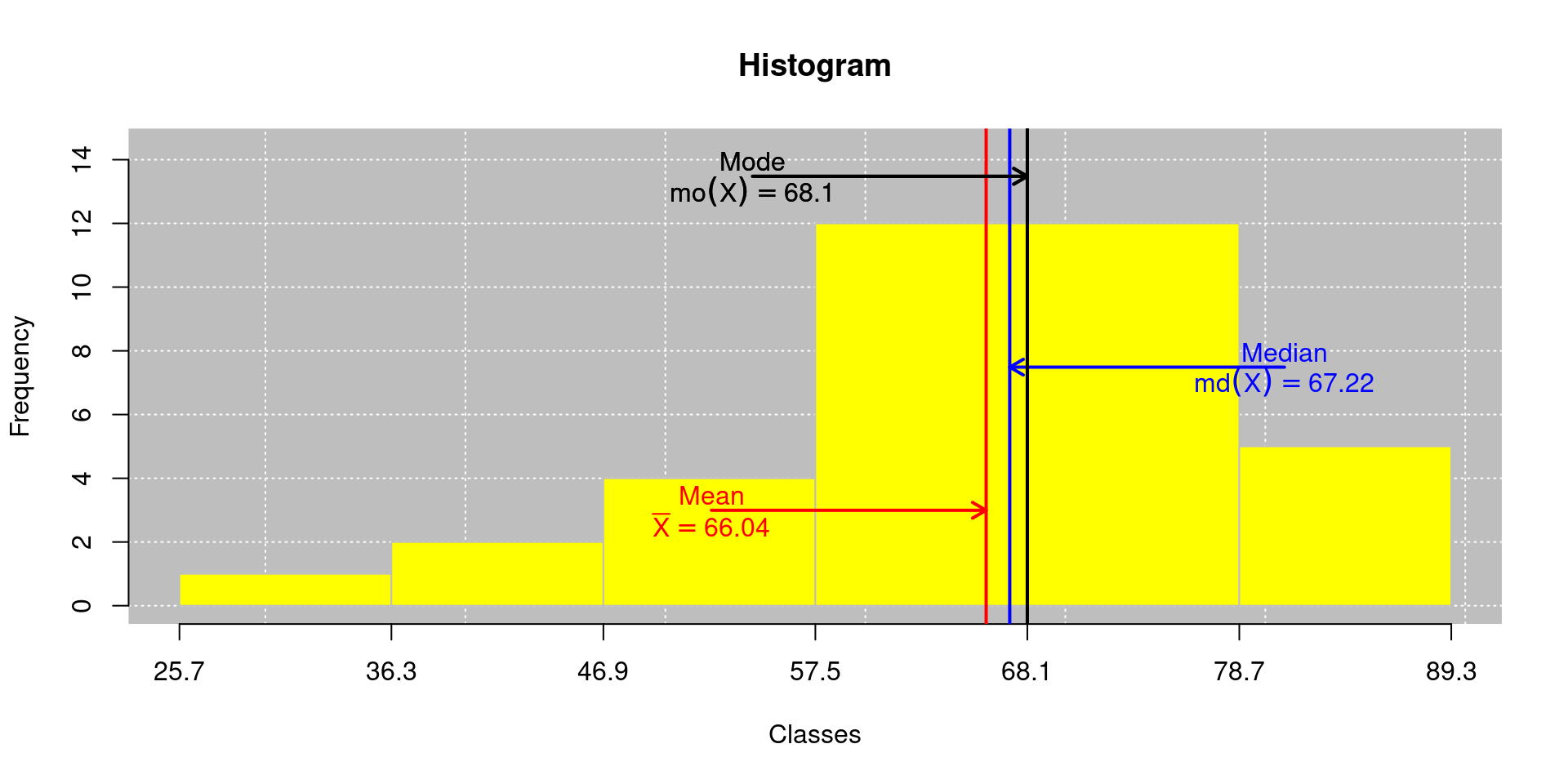
\[\begin{align*} \bar{X} & = \sum_{i=1}^{k}\tilde{X}_if_i / \sum_{i=1}^{k}f_i \\ & = \frac{31 \times 1 + \ldots + 41.6 \times 2}{36}\\ & = 66,04~\textrm{°F}. \end{align*}\]


Table of frequency 
Type of variable: continuous

          Classes Fi   PM   Fr Fac1 Fac2 Fp  Fac1p  Fac2p
1 25.7 |---  36.3  1 31.0 0.03    1   36  3   2.78 100.00
2 36.3 |---  46.9  2 41.6 0.06    3   35  6   8.33  97.22
3 46.9 |---  57.5  4 52.2 0.11    7   33 11  19.44  91.67
4 57.5 |---  68.1 12 62.8 0.33   19   29 33  52.78  80.56
5 68.1 |---  78.7 12 73.4 0.33   31   17 33  86.11  47.22
6 78.7 |---  89.3  5 84.0 0.14   36    5 14 100.00  13.89

============================================== 
Classes: Grouping of classes 
Fi: Absolute frequency 
PM: Midpoint 
Fr: Relative frequency 
Fac1: Cumulative frequency (below) 
Fac2: Cumulative frequency (above) 
Fp: Percentage frequency 
Fac1p: Cumulative percentage frequency (below) 
Fac2p: Cumulative percentage frequency (above)

Usando o leem

  • Exemplo 1 - Número de erros
  • Exemplo 2 - Challenger
  • Funções: new_leem(), tabfreq(), mean(), insert()
dado |> # Entrada dos dados
  new_leem() |> # Estruturando os dados a classe leem
  # Opções:
  #   new_leem(variable = 1) # => variável discreta
  #   new_leem(variable = 2) # => variável contínua
  tabfreq() |> # Distribuição de frequência
  mean() # Cálculo da média
  # Opções:
  #   mean(grouped = TRUE) # => Dados agrupados (Padrão)
  #   mean(grouped = FALSE) # => Dados não agrupados

Usando o leem (continuação…)

Exemplo 1 - Com agrupamento

d1 |>
  new_leem(variable = 1) |>
  tabfreq() |>
  mean()
[1] 1.7

Exemplo 1 - Sem agrupamento

d1 |>
  new_leem(variable = 1) |>
  tabfreq() |>
  mean(grouped = FALSE)
[1] 1.7

Usando o leem (continuação…)

Exemplo 2 - Com agrupamento

d2 |>
  new_leem(variable = 2) |>
  tabfreq() |>
  mean()
[1] 66.04

Exemplo 2 - Sem agrupamento

d2 |>
  new_leem(variable = 2) |>
  tabfreq() |>
  mean(grouped = FALSE)
[1] 65.86

Usando o leem (continuação…)

Verificando a média no histograma:

d2 |>
  new_leem(variable = 2) |>
  tabfreq() |>
  hist() |>
  insert(type = "mean", side = "left")

Características da média

  • a unidade da média está na mesma escala da variável em estudo;
  • a média é uma das medidas mais conhecidas e utilizadas, devido as suas propriedades estatísticas que serão vistas nos capítulos seguintes;
  • é única para cada conjunto de dados;
  • usada apenas para variáveis quantitativas;
  • não pode ser calculada para dados agrupados que apresentam classes extremas abertas;
  • é influenciada por dados discrepantes.

Propriedades da média

Teorema: Baseado na Definição sobre a média, e considerando \(c\) uma constante, então:

  • Se para uma amostra \(X_1\), \(X_2\), \(\ldots\), \(X_n\), a média aritmética é dada por \(\bar{X} = \frac{\sum_{i=1}^{n}X_i}{n}\), então para uma transformação de \(Y_i = X_i \pm c\), para \(i\) \(=\) \(1\), \(2\), \(\ldots\), \(n\), a nova média aritmética é dada por \(\bar{Y} = \bar{X} \pm c\);

  • Se para uma amostra \(X_1\), \(X_2\), , \(X_n\), a média aritmética é dada por \(\bar{X} = \frac{\sum_{i=1}^{n}X_i}{n}\), então para uma transformação de \(Y_i = X_i \times c\), para \(i\) \(=\) \(1\), \(2\), \(\ldots\), \(n\), a nova média aritmética é dada por \(\bar{Y} = \bar{X} \times c\). Esse resultado vale também para a transformação \(Y_i = X_i / m\), sendo \(m\) também uma constante. Basta usar \(c = 1 / m\) e o resultado é o mesmo.

  • A soma de quadrado de desvios dos dados em relação a uma constante \(c\), é minimizada se \(c = \bar{X}\).

Mediana

Definição (Mediana): Seja uma amostra \(X_1\), \(X_2\), \(\ldots\), \(X_n\), de uma população \(X_1\), \(X_2\), \(\ldots\), \(X_N\), de tamanhos \(n\) e \(N\), respectivamente, definimos a mediana por: \[\begin{align*} \mu_d(X) & = \left\{\begin{array}{ll} \frac{X_{(\frac{N}{2})} + X_{\left( \frac{N}{2} + 1 \right)}}{2}, & \textrm{se } N \textrm{ for par} \\ & \\ X_{(\frac{N + 1}{2})}, & \textrm{se } N \textrm{ for ímpar} \\ \end{array}\right., \quad \textrm{(População)} \end{align*}\]

Mediana (continuação…)

(Continuação…): sendo \(\mu_d(X)\) a mediana populacional e que \(X_{(i)}\) é a \((i)\)-ésima variável em ordem crescente de magnitude, tal que \(X_{(1)} = \min\limits_{i}(X_i)\) e \(X_{(n)} = \max\limits_{i}(X_i)\). De modo similar, \[\begin{align*} Md(X) & = \left\{\begin{array}{ll} \frac{X_{(\frac{n}{2})} + X_{\left( \frac{n}{2} + 1 \right)}}{2}, & \textrm{se } n \textrm{ for par} \\ & \\ X_{(\frac{n + 1}{2})}, & \textrm{se } n \textrm{ for ímpar} \\ \end{array}\right., \quad \textrm{(Amostra)} \end{align*}\] sendo \(Md(X)\) a mediana amostral e que \(X_{(i)}\) é a \((i)\)-ésima variável em ordem crescente de magnitude, tal que \(X_{(1)} = \min\limits_{i}(X_i)\) e \(X_{(n)} = \max\limits_{i}(X_i)\).

Mediana (Agrupamento com classes)

Definição (Mediana): Seja uma amostra \(X_{(1)}\), \(X_{(2)}\), \(\ldots\), \(X_{(n)}\) em ordem crescente de magnitude, de tamanho \(n\), agrupados em \(k\) classes com pontos médios \(\tilde{X}_i\) e \(F_i\) frequências, para \(i\) \(=\) \(1\), \(2\), \(\ldots\), \(k\) e \(\sum_{i = 1}^{k}F_i = n\), então a mediana amostral é definida por: \[\begin{align*} Md(X) = LI_{Md} + \left\lbrace \frac{\frac{n}{2}-f_{ant}}{f_{Md}}\right\rbrace \times c. \end{align*}\] em que \(LI_{Md}\) é o limite inferior da classe da mediana, \(f_{ant}\) é a frequência acumulada (abaixo de) anterior a classe da mediana, \(f_{Md}\) frequência absoluta da classe da mediana, \(c\) a amplitude da classe da mediana,

Mediana (continuação…)

(continuação…): ou de forma similar, \[\begin{align*} Md(X) = LS_{Md} - \left\lbrace \frac{\frac{n}{2}-f_{post}}{f_{Md}} \right\rbrace \times c. \end{align*}\] em que \(LS_{Md}\) é o limite superior da classe da mediana e \(f_{post}\) é a frequência acumulada (acima de) posterior a classe da mediana.

Exemplo 1 - Número de erros

Dados do número de erros encontrados em 20 conjuntos de caracteres monitorado em um canal de comunicação.

3 1 0 1 3 2 4 1 3 1
1 1 2 3 3 2 0 2 0 1

Ordenando os dados, temos:

0 0 0 1 1 1 1 1 1 1
2 2 2 2 3 3 3 3 3 4

Calculando a mediana, temos:

\[\begin{align*} Md(X) = \frac{X_{(\frac{20}{2})} + X_{\left( \frac{20}{2} + 1 \right)}}{2} = \frac{X_{(10)} + X_{(11)}}{2} = \frac{1 + 2}{2} = 1,5~\textrm{erros}. \end{align*}\]

Exemplo 2 - Challenger

Os dados representam a temperatura (°F) do anel de vedação de cada teste de acionamento ou lançamento real do motor do foguete Challenger

84 40 45 69 68 72 57 78 53 61 76 76
49 83 66 80 60 73 63 52 67 70 79 58
61 67 70 58 67 70 70 67 75 81 75 31

Ordenando os dados, temos:

31 40 45 49 52 53 57 58 58 60 61 61
63 66 67 67 67 67 68 69 70 70 70 70
72 73 75 75 76 76 78 79 80 81 83 84

Exemplo (continuação…)

Retornando o exemplo anterior…

Sem agrupamento, temos:

\[\begin{align*} Md(X) & = \frac{X_{(\frac{36}{2})} + X_{\left( \frac{36}{2} + 1 \right)}}{2}\\ & = \frac{X_{(18)} + X_{(19)}}{2} = \frac{67 + 68}{2}\\ & = 67,5~\textrm{°F}. \end{align*}\]

Com o agrupamento, temos:

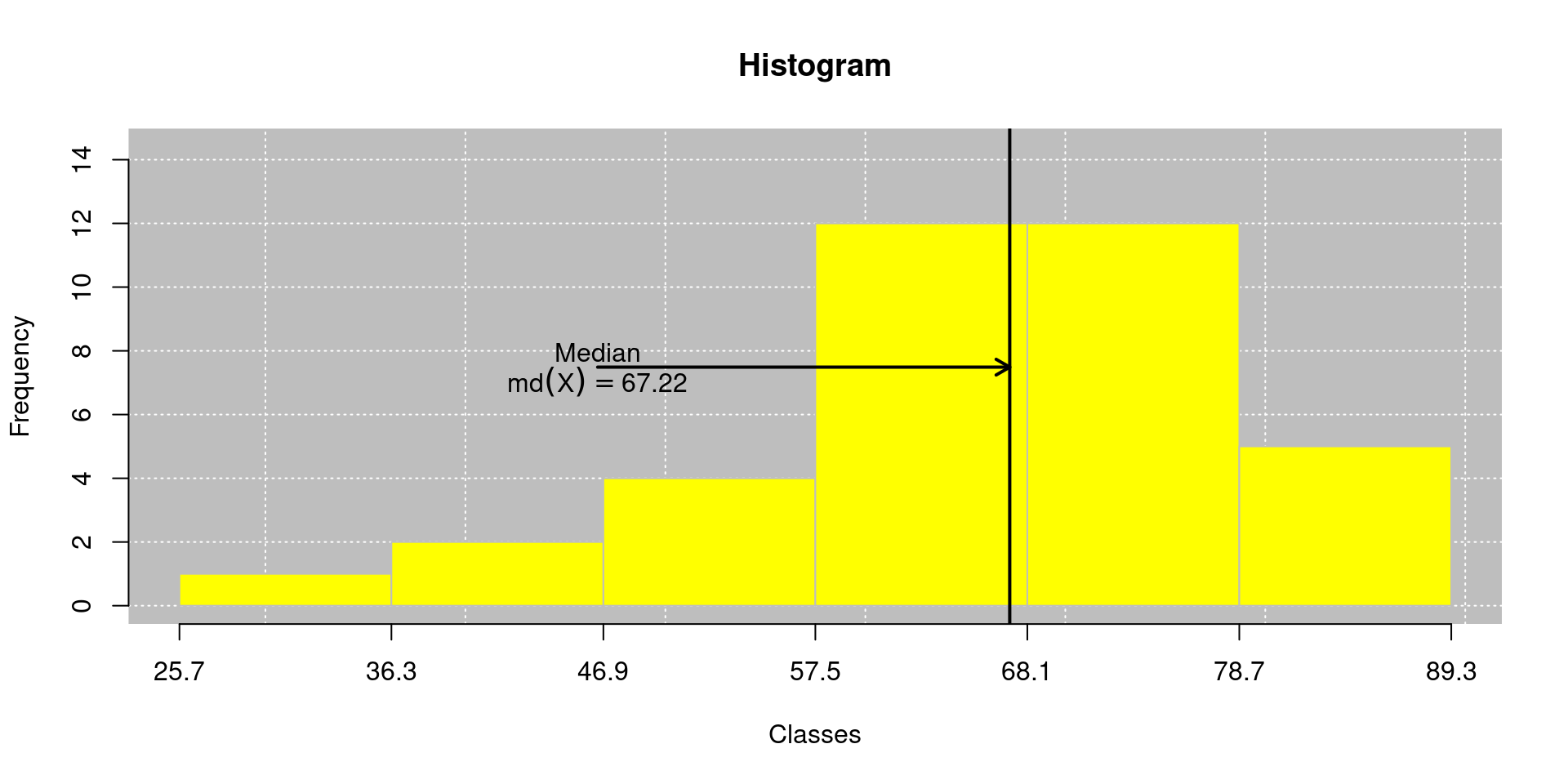
\[\begin{align*} Md(X) & = LI_{Md} + \left\lbrace \frac{\frac{n}{2}-f_{ant}}{f_{Md}}\right\rbrace \times c \\ & = 57,5 + \left\lbrace \frac{\frac{36}{2}-7}{12}\right\rbrace \times (68,1 - 57,5)\\ & = 57,5 + \left\lbrace \frac{18-7}{12}\right\rbrace \times (10,6)\\ & = 67,22~\textrm{°F}. \end{align*}\]


Table of frequency 
Type of variable: continuous

          Classes Fi   PM   Fr Fac1 Fac2 Fp  Fac1p  Fac2p
1 25.7 |---  36.3  1 31.0 0.03    1   36  3   2.78 100.00
2 36.3 |---  46.9  2 41.6 0.06    3   35  6   8.33  97.22
3 46.9 |---  57.5  4 52.2 0.11    7   33 11  19.44  91.67
4 57.5 |---  68.1 12 62.8 0.33   19   29 33  52.78  80.56
5 68.1 |---  78.7 12 73.4 0.33   31   17 33  86.11  47.22
6 78.7 |---  89.3  5 84.0 0.14   36    5 14 100.00  13.89

============================================== 
Classes: Grouping of classes 
Fi: Absolute frequency 
PM: Midpoint 
Fr: Relative frequency 
Fac1: Cumulative frequency (below) 
Fac2: Cumulative frequency (above) 
Fp: Percentage frequency 
Fac1p: Cumulative percentage frequency (below) 
Fac2p: Cumulative percentage frequency (above)

Usando o leem

  • Exemplo 1 - Número de erros
  • Exemplo 2 - Challenger
  • Funções: new_leem(), tabfreq(), median(), insert()

dado |> # Entrada dos dados
  new_leem() |> # Estruturando os dados a classe leem
  # Opções:
  #   new_leem(variable = 1) # => variável discreta
  #   new_leem(variable = 2) # => variável contínua
  tabfreq() |> # Distribuição de frequência
  median() # Cálculo da mediana
  # Opções:
  #   median(grouped = TRUE) # => Dados agrupados (Padrão)
  #   median(grouped = FALSE) # => Dados não agrupados

Usando o leem (continuação…)

Exemplo 1 - Com agrupamento

d1 |>
  new_leem(variable = 1) |>
  tabfreq() |>
  median()
[1] 1.5

Exemplo 1 - Sem agrupamento

d1 |>
  new_leem(variable = 1) |>
  tabfreq() |>
  median(grouped = FALSE)
[1] 1.5

Usando o leem (continuação…)

Exemplo 2 - Com agrupamento

d2 |>
  new_leem(variable = 2) |>
  tabfreq() |>
  median()
[1] 67.22

Exemplo 2 - Sem agrupamento

d2 |>
  new_leem(variable = 2) |>
  tabfreq() |>
  median(grouped = FALSE)
[1] 67.5

Usando o leem (continuação…)

Verificando a mediana no histograma:

d2 |>
  new_leem(variable = 2) |>
  tabfreq() |>
  hist() |>
  insert(type = "median", side = "left")

Características da mediana

  • A mediana não é influenciada por valores extremos;
  • Uma medida que pode ser obtida em distribuições de frequências que apresentam classe com limites indefinidos;
  • o resultado da mediana é obtida na mesma escala da variavel em estudo;
  • a mediana é menos informativa que a média, por não levar em consideração os valores observados, mas as posições dessas observações;
  • a mediana pode ser calculada em variáveis qualitativas ordinais, cuja média não pode ser obtida;
  • a mediana ainda pode ser obtida em um conjunto de dados em que alguns valores ainda não foram registrados, caso em que a média não pode ser obtida.

Propriedades da mediana

Teorema: Baseado na Definição sobre a mediana, e considerando \(c\) uma constante, então:

  • Se para uma amostra \(X_{(1)}\), \(X_{(2)}\), \(\ldots\), \(X_{(n)}\) em ordem crescente de magnitude, a mediana é dada por \(Md{X} = X_{(\frac{n + 1}{2})}\), então para uma transformação de \(Y_i = X_i \pm c\), para \(i\) \(=\) \(1\), \(2\), \(\ldots\), \(n\), a mediana aritmética é dada por \(Md(Y) = Md(X) \pm c\);
  • Se para uma amostra \(X_{(1)}\), \(X_{(2)}\), \(\ldots\), \(X_{(n)}\) em ordem crescente de magnitude, a mediana é dada por \(Md(X) = X_{(\frac{n + 1}{2})}\), então para uma transformação de \(Y_i = X_i \pm c\), para \(i\) \(=\) \(1\), \(2\), \(\ldots\), \(n\), a nova mediana é dada por \(Md(Y) = Md(X) \times c\). Esse resultado vale também para a transformação \(Y_i = X_i / m\), sendo \(m\) também uma constante. Basta usar \(c = 1 / m\) e o resultado é o mesmo.
  • A soma do módulo dos desvios dos dados em relação a uma constante arbitrária \(c\), terá um valor mínimo se \(c=Md(X)\).

Moda

Definição (Moda para dados discretizados): Seja uma amostra \(X_1\), \(X_2\), \(\ldots\), \(X_n\), de uma população \(X_1\), \(X_2\), \(\ldots\), \(X_N\), de tamanhos \(n\) e \(N\), respectivamente, cuja natureza da variável é discretizada. Então a moda representa o valor que mais se repete em um conjunto de dados. Denotamos \(\mu_o\) a moda populacional, e \(Mo(X)\) a moda amostral.

Moda (Agrupamento com classes)

Definição (Moda): Seja uma amostra \(X_{(1)}\), \(X_{(2)}\), \(\ldots\), \(X_{(n)}\) em ordem crescente de magnitude, de tamanho \(n\), agrupados em \(k\) classes com pontos médios \(\tilde{X}_i\) e \(F_i\) frequências, para \(i\) \(=\) \(1\), \(2\), \(\ldots\), \(k\) e \(\sum_{i = 1}^{k}F_i = n\), então a moda amostral é definida por: \[\begin{align} Mo(X) & = LI_{Mo} + \left\lbrace \frac{\Delta_1}{\Delta_1 + \Delta_2}\right \rbrace \times c, \end{align}\] em que \(LI_{Mo}\) o limite inferior da classe da moda, \(\Delta_1 = f_{Mo} - f_{i_{ant}}\), \(\Delta_2 = f_{Mo} - f_{i_{post}}\), \(f_{Mo}\) é a frequência absoluta da classe da moda, \(f_{i_{ant}}\) frequência absoluta anterior à classe da moda, \(f_{i_{post}}\) frequência posterior à classe da moda, e \(c\) a amplitude da classe.

Exemplo 1 - Número de erros

Dados do número de erros encontrados em 20 conjuntos de caracteres monitorado em um canal de comunicação.

3 1 0 1 3 2 4 1 3 1
1 1 2 3 3 2 0 2 0 1

Calculando a moda, temos:

\[\begin{align*} Mo(X) = 1,0~\textrm{erros}. \end{align*}\]

Exemplo 2 - Challenger

Os dados representam a temperatura (°F) do anel de vedação de cada teste de acionamento ou lançamento real do motor do foguete Challenger

84 40 45 69 68 72 57 78 53 61 76 76
49 83 66 80 60 73 63 52 67 70 79 58
61 67 70 58 67 70 70 67 75 81 75 31

Ordenando os dados, temos:

31 40 45 49 52 53 57 58 58 60 61 61
63 66 67 67 67 67 68 69 70 70 70 70
72 73 75 75 76 76 78 79 80 81 83 84

Exemplo (continuação…)

Retornando o exemplo anterior…

Sem agrupamento, temos:

\[\begin{align*} Mo(X) & = 67~\textrm{°F},~70~\textrm{°F}. \end{align*}\]

Com o agrupamento, temos:

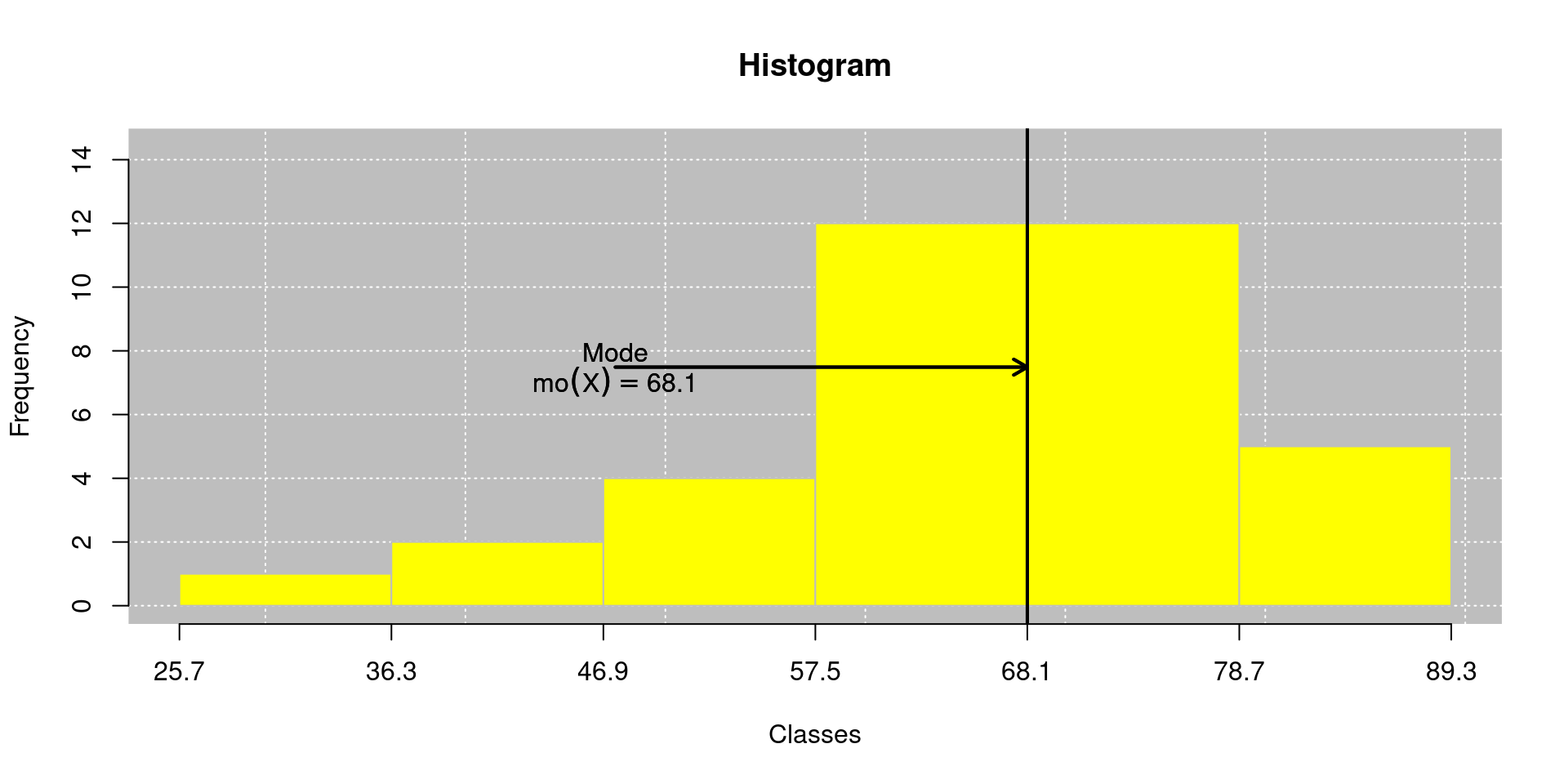
\[\begin{align*} Mo(X)_1 & = LI_{Mo} + \left\lbrace \frac{\Delta_1}{\Delta_1 + \Delta_2}\right \rbrace \times c \\ & = 57,5 + \left\lbrace \frac{12 - 4}{(12 - 4) + (12 - 12)}\right\rbrace \times (68,1 - 57,5)\\ & = 68,1~\textrm{°F}. \end{align*}\]

\[\begin{align*} Mo(X)_2 & = LI_{Mo} + \left\lbrace \frac{\Delta_1}{\Delta_1 + \Delta_2}\right \rbrace \times c \\ & = 68,1 + \left\lbrace \frac{12 - 12}{(12 - 12) + (12 - 5)}\right\rbrace \times (68,1 - 57,5)\\ & = 68,1~\textrm{°F}. \end{align*}\]


Table of frequency 
Type of variable: continuous

          Classes Fi   PM   Fr Fac1 Fac2 Fp  Fac1p  Fac2p
1 25.7 |---  36.3  1 31.0 0.03    1   36  3   2.78 100.00
2 36.3 |---  46.9  2 41.6 0.06    3   35  6   8.33  97.22
3 46.9 |---  57.5  4 52.2 0.11    7   33 11  19.44  91.67
4 57.5 |---  68.1 12 62.8 0.33   19   29 33  52.78  80.56
5 68.1 |---  78.7 12 73.4 0.33   31   17 33  86.11  47.22
6 78.7 |---  89.3  5 84.0 0.14   36    5 14 100.00  13.89

============================================== 
Classes: Grouping of classes 
Fi: Absolute frequency 
PM: Midpoint 
Fr: Relative frequency 
Fac1: Cumulative frequency (below) 
Fac2: Cumulative frequency (above) 
Fp: Percentage frequency 
Fac1p: Cumulative percentage frequency (below) 
Fac2p: Cumulative percentage frequency (above)

Usando o leem

  • Exemplo 1 - Número de erros
  • Exemplo 2 - Challenger
  • Funções: new_leem(), tabfreq(), mfreq(), insert()

dado |> # Entrada dos dados
  new_leem() |> # Estruturando os dados a classe leem
  # Opções:
  #   new_leem(variable = 1) # => variável discreta
  #   new_leem(variable = 2) # => variável contínua
  tabfreq() |> # Distribuição de frequência
  mfreq() # Cálculo da média
  # Opções:
  #   mfreq(grouped = TRUE) # => Dados agrupados (Padrão)
  #   mfreq(grouped = FALSE) # => Dados não agrupados

Usando o leem (continuação…)

Exemplo 1 - Com agrupamento

d1 |>
  new_leem(variable = 1) |>
  tabfreq() |>
  mfreq()
[1] 1

Exemplo 1 - Sem agrupamento

d1 |>
  new_leem(variable = 1) |>
  tabfreq() |>
  mfreq(grouped = FALSE)
[1] 1

Usando o leem (continuação…)

Exemplo 2 - Com agrupamento

d2 |>
  new_leem(variable = 2) |>
  tabfreq() |>
  mfreq()
[1] 68.1 68.1

Exemplo 2 - Sem agrupamento

d2 |>
  new_leem(variable = 2) |>
  tabfreq() |>
  mfreq(grouped = FALSE)
[1] 67 70

Usando o leem (continuação…)

Verificando a moda no histograma:

d2 |>
  new_leem(variable = 2) |>
  tabfreq() |>
  hist() |>
  insert(type = "mode", side = "left")

Usando o leem (continuação…)

Rearrajando as classes …

d2 |>
  new_leem(variable = 2) |>
  tabfreq(k = 5) # Apenas com 5 classes

Table of frequency 
Type of variable: continuous

            Classes Fi    PM   Fr Fac1 Fac2 Fp  Fac1p  Fac2p
1 24.38 |---  37.62  1 31.00 0.03    1   36  3   2.78 100.00
2 37.62 |---  50.88  3 44.25 0.08    4   35  8  11.11  97.22
3 50.88 |---  64.12  9 57.50 0.25   13   32 25  36.11  88.89
4 64.12 |---  77.38 17 70.75 0.47   30   23 47  83.33  63.89
5 77.38 |---  90.62  6 84.00 0.17   36    6 17 100.00  16.67

============================================== 
Classes: Grouping of classes 
Fi: Absolute frequency 
PM: Midpoint 
Fr: Relative frequency 
Fac1: Cumulative frequency (below) 
Fac2: Cumulative frequency (above) 
Fp: Percentage frequency 
Fac1p: Cumulative percentage frequency (below) 
Fac2p: Cumulative percentage frequency (above)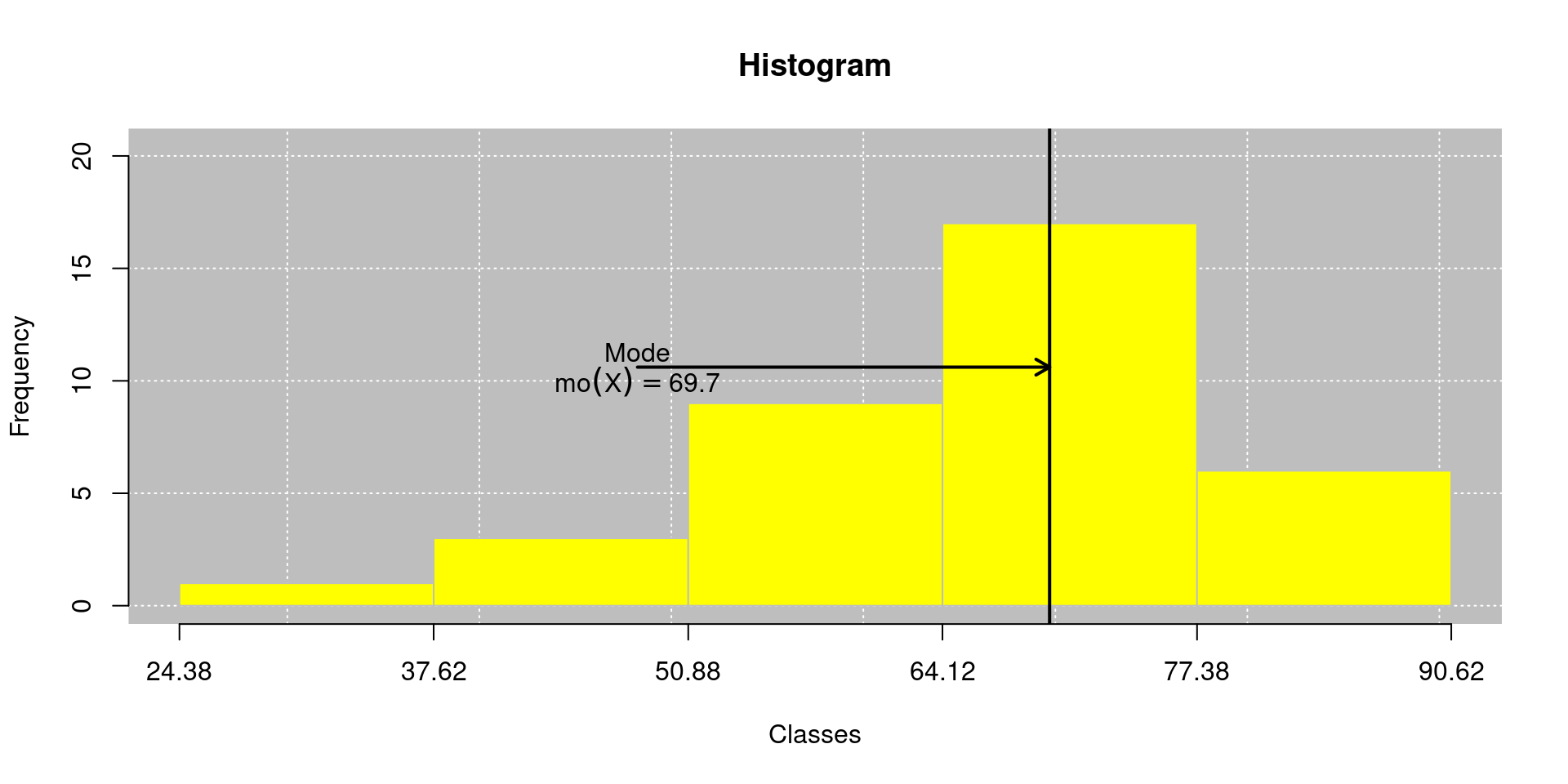

Características da moda

  • A moda não é influenciada por valores extremos, desde que estes não pertençam a classe modal;
  • Uma medida que pode ser obtida em distribuições de frequências que apresentam classe com limites indefinidos;
  • o resultado da moda é obtida na mesma escala da variavel em estudo;
  • a moda é menos informativa que a média, por não levar em consideração os valores observados;
  • a moda pode ser calculada para todas as naturezas de variáveis;
  • a moda é a medida mais simples dentre as apresentadas;

Propriedades da moda

Teorema: Baseado na Definição sobre a moda, e considerando \(c\) uma constante, então:

  • Se para uma amostra \(X_1\), \(X_2\), , \(X_n\) em ordem crescente de magnitude, a moda representa o valor de maior frequência e representado por \(Mo(X)\), então para uma transformação de \(Y_i = X_i \pm c\), para \(i\) \(=\) \(1\), \(2\), \(\ldots\), \(n\), a moda é dada por \(Mo(Y) = Mo(X) \pm c\);
  • Se para uma amostra \(X_1\), \(X_2\), , \(X_n\) em ordem crescente de magnitude, a moda representa o valor de maior frequência e representado por \(Mo(X)\), então para uma transformação de \(Y_i = X_i \pm c\), para \(i\) \(=\) \(1\), \(2\), \(\ldots\), \(n\), a nova moda é dada por \(Mo(Y) = Mo(X) \times c\). Esse resultado vale também para a transformação \(Y_i = X_i / m\), sendo \(m\) também uma constante. Basta usar \(c = 1 / m\) e o resultado é o mesmo.

Usando o leem

Inserindo as três medidas no histograma:

d2 |>
  new_leem(variable = 2) |>
  tabfreq() |>
  hist() |>
  insert(type = "all", larrow = 0.4, lcol = c("red", "blue", "black"))

Questões?

Dúvidas e Sugestões

Contato

Próximas aulas
bendeivide.github.io/courses/epaec

Referências

EPAEC | https://bendeivide.github.io/

BATISTA, B. D. O. Estatística e Probabilidade: Aplicada às Engenharias e Ciências. Ouro Branco, MG, Brasil: [s.n.], 2023.