Estatística e Probabilidade

Aula 14- Distribuições de probabilidade (Parte I)

Ben Dêivide | UFSJ

Filosofia de publicação (Selo DC)

Livro de Apoio

Usaremos Batista (2023):

Introdução

• Distribuição Binomial
• Distribuição Poisson

Distribuição Binomial

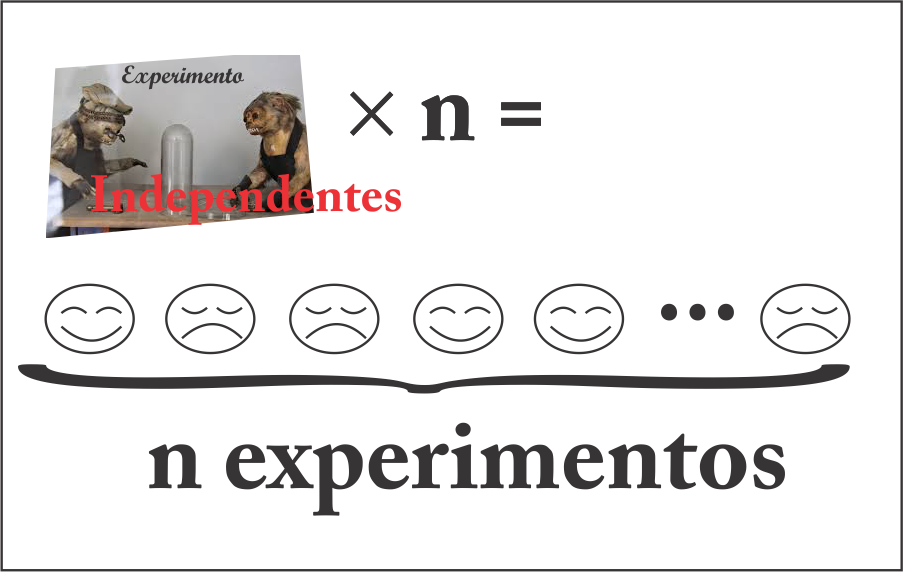
Exemplo

Um produto eletrônico contém 40 circuitos integrados, que opera de modo independente. A probabilidade que algum circuito integrado tenha defeito é 0,01. O produto somente funcionará se não houver defeito em nenhum circuito integrado. Então, qual a probabilidade que o produto funcione corretamente?

Características

• \(n\) experimentos Bernoulli
• \(X \sim Binomial(n,p)\) \(\Rightarrow\) \(S_X = \{0, 1, 2, \ldots, n\}\)
• Esperança: \(\mu_X = E[X] = np\)
• Variância: \(\sigma^2_X = Var[X] = np(1-p)\)
• Função de distribuição: \(F_X(x^*) = \sum_{x \leq x^*}\binom{n}{x}p^x(1-p)^{n-x}\)
• Às vezes, é melhor: \(P(X\leq x) = 1 - P(X > x)\)

Graficamente

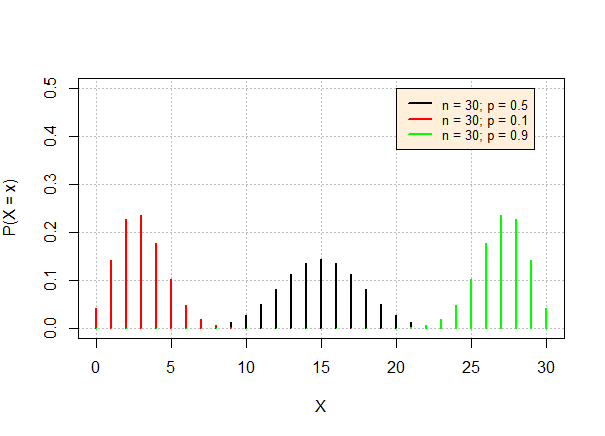
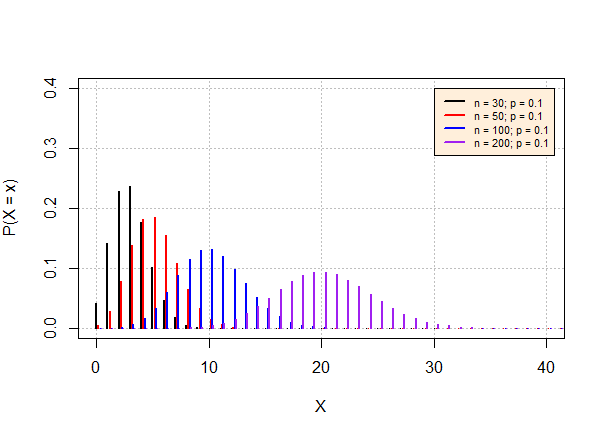
Funções leem

Função	Finalidade
P()	Função distribuição
Q()	Função quantil
pf()	Função de probabilidade

Para todas elas, devemos usar o argumento dist="binomial"

Distribuição Poisson

Distribuição Poisson

Uma variável aleatória \(X\) discreta, tem distribuição Poisson , se sua função de probabilidade é dada por \[\begin{eqnarray}\label{eq:distpoisson} P(X=x)=\left\lbrace \begin{array}{ll} \frac{e^{-\lambda}\lambda^{x}}{x!},& \textrm{ para } x= 0,1,2,\ldots,\\ 0,& \textrm{caso contrário}, \end{array}\right. \end{eqnarray}\] em que \(\lambda>0\). Em notação, \(X \sim Poisson(\lambda)\) representa que \(X\) tem distribuição Poisson com parâmetro \(\lambda\).

Exemplo

Os fios de cobre são muito utilizados em sistemas elétricos pela sua excelente condutividade elétrica, e apresentar uma resistência elétrica mais baixa entre todos os metais não-preciosos. Seja um experimento que observa as falhas de transmissão de um fio de cobre, e sabe-se que:

• \(\lambda\) = 2,3 falhas/mm;
• \(X\) é uma variável aleatória que denota o número de falhas em cada 1 mm de cobre;
• \(P(X = 2~falhas/mm)\);
• \(P(X = 10~falhas/5mm)\).

Características

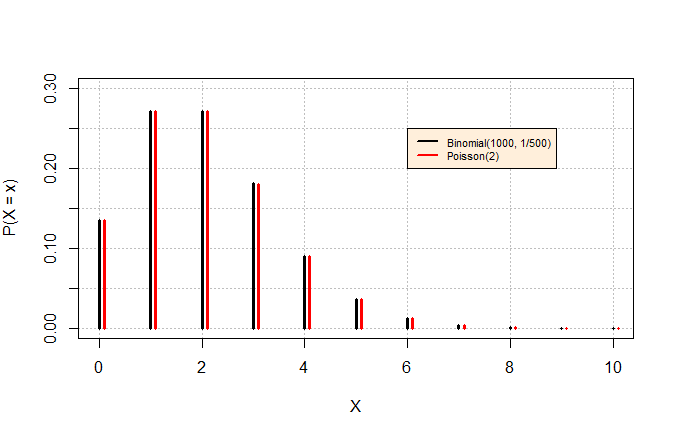
• \(X \sim Binomial(n,p)\), \(n \to \infty\), \(p \to 0\) \(\Rightarrow\) \(X \sim Poisson(\lambda)\)
  • \(\lambda = np\)
• \(X \sim Poisson(\lambda)\) \(\Rightarrow\) \(S_X = \{0, 1, 2, \ldots\}\)
• Esperança: \(\mu_X = E[X] = \lambda\)
• Variância: \(\sigma^2_X = Var[X] = \lambda\) (Superdispersão)
• Função de distribuição: \(F_X(x^*) = \sum_{x \leq x^*}\lambda^x \times e^{-\lambda x} / x!\)
• Às vezes, é melhor: \(P(X > x) = 1 - P(X\leq x)\)

Graficamente

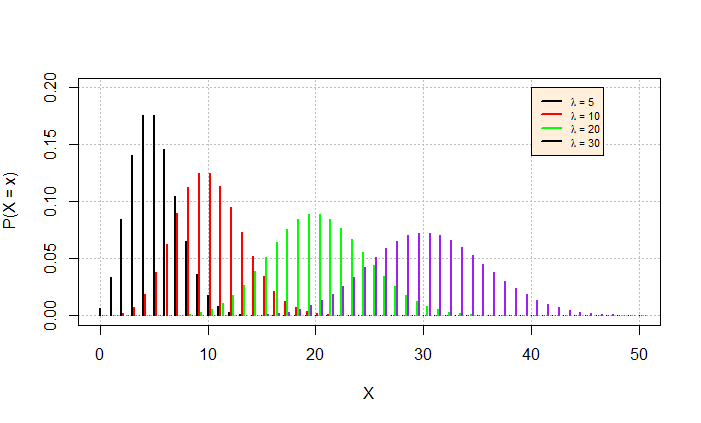
Funções leem

Função	Finalidade
P()	Função distribuição
Q()	Função quantil
pf()	Função de probabilidade

Para todas elas, devemos usar o argumento dist="poisson"

Próximas aulas

bendeivide.github.io/courses/epaec

Referências

BATISTA, B. D. O. Estatística e Probabilidade: Aplicada às Engenharias e Ciências. Ouro Branco, MG, Brasil: [s.n.], 2023.