Estatística e Probabilidade
Aula 11 - Probabilidades
Selo DC
Teoria de conjuntos no contexto probabilístico
Todo experimento cujo resultado não pode ser previsto antes de sua execução, é chamado de experimento aleatório.
Exemplos
Lançar um dado equilibrado e observar o resultado obtido na face superior do dado.
Observar o número de chamadas telefônicas que chegam a uma central telefônica em um determinado intervalo de tempo.
Para a escolha ao acaso de uma lâmpada que acabou de sair do processo de fabricação, verificar o tempo de duração da lâmpada em funcionamento.
Experimento aleatório
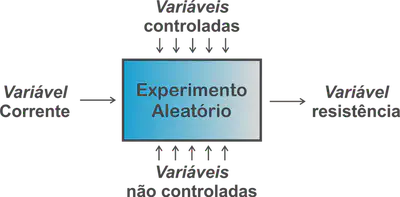
Em um contexto aplicado, podemos estar interessados em estudar a resistência de um fio de cobre a uma determinada corrente
Espaço amostral
O conjunto de todos os resultados possíveis de um experimento, denotado por $ \Omega $, é chamado de espaço amostral.
- Cada um dos elementos do espaço amostral é representado por
\(\omega\); - Relações:
- Pertinência:
\(\omega \in \Omega\); - Continência:
\(A \subset B \Leftrightarrow \omega \in A \Rightarrow \omega \in B\); - Equivalência:
\(A = B \Leftrightarrow A \subset B \textrm{ e } B \subset A\).
- Pertinência:
Espaços amostrais discretos e contínuos
Um espaço amostral é discreto se o conjunto dos possíveis resultados são finito ou infinito contável (ou enumerável). Um espaço amostral é dito contínuo se o conjunto dos possíveis resultados são infinitos não contável (ou não enumerável).
Exemplo
Considere um experimento em que você seleciona uma câmera de telefone celular e registra o tempo de recarga de um flash. Os resultados possíveis para o tempo dependem da resolução do temporizador e dos tempos máximo e mínimo de recarga. Entretanto, podemos definir inicialmente o espaço amostral em termos da reta real positiva ($\mathbb{R}_+$), isto é,
\begin{align*} \Omega = \mathbb{R}_+ & = \{ x ~:~ x > 0\}. \end{align*}Se soubermos que os tempos de recarga estão entre $ 1,5 $ e $ 5 $ segundos, podemos definir o espaço amostral da seguinte forma:
\begin{align*} \Omega & = \{ x ~:~ 1,5 \leq x \leq 5\}. \end{align*}Caso, consideremos o tempo de recarga como "baixo", "médio" ou "alto", reescrevemos o espaço amostral como:
\begin{align*} \Omega & = \{ \textrm{baixo}, \textrm{médio}, \textrm{alto} \}. \end{align*}Exemplo (continuação...)
Por fim, podemos considerar apenas o fato da câmera satisfazer ou não as especificações do tempo de recarga mínimo, e assim, podemos assumir como resultados para esse espaço amostral: "sim" ou não", isto é,
\begin{align*} \Omega & = \{\textrm{sim},~\textrm{não}\}. \end{align*}Para as duas primeiras situações, temos exemplos de espaços amostrais contínuos, e nos dois últimos, exemplos de espaços amostrais discretos.
Subconjunto
Se todo elemento do conjunto A é também elemento do conjunto B, então A é definido como um subconjunto de B, sendo representado $ A\subset B $ ou $ B\supset A $ (A está contido em B ou B contém A), em notação dizemos que:
\begin{align*} A \subset B \Leftrightarrow A \subseteq B \textrm{ e } A \neq B. \end{align*}- Essa definição pode ser aplicada também a subconjuntos de $ \Omega $, como apresentado no Exemplo sobre subconjuntos, a seguir.
Exemplo
Sejam os subconjuntos de $ \Omega $ do experimento aleatório apresentado no Exemplo sobre espaços amostrais, dos quais temos:
\begin{align*} B=\{ 1,2,3,4 \} \ \mbox{ e } \ A= \{ 1,2,3 \}, \end{align*}então A é um subconjunto de B, pois, os elementos que contém em A, também contém em B.
Evento
Todo subconjunto do espaço amostral ($ \Omega $), representado por letras latinas em maiúsculo, A, B, $ \ldots $, é chamado de evento.
Exemplo
Um experimento lança três moedas honestas, e deseja-se verificar a face superior dessas moedas. Sabe-se que cada moeda apresenta duas faces: cara (H) e coroa (T). Dessa forma, o espaço amostral é dado por:
\begin{align*} \Omega = &\{(H,H,H),(H,H,T),(H,T,H),(H,T,T),\\ & (T,H,H),(T,H,T),(T,T,H),(T,T,T)\}. \end{align*}Um evento retirado desse espaço amostral seria $ A=\{(H,H,H) $, $ (H,H,T) $, $ (H,T,T) \} $, ou seja, o evento em que dos três arremessos de moedas, tenha saído "cara" na primeira moeda.
Evento certo, impossível e elementar
Seja $ \Omega $ o espaço amostral do experimento. Então dizemos que $ \Omega $ é o evento certo, e $ \emptyset $ é o evento impossível, e o evento $ \{\omega\} $ é dito elementar.
Conjunto vazio
Se o conjunto A não contém nenhum elemento, então A é chamado de conjunto nulo ou conjunto vazio, ou seja, $ A=\varnothing $ ou $ A=\{ \ \} $, isto é,
\begin{align*} A & = \{\omega \in \Omega: \omega \neq \omega \}. \end{align*}União de dois eventos
Sejam A e B, dois eventos quaisquer de $ \Omega $, então o conjunto de todos os elementos que estão em A ou B ou em ambos, é definido como o conjunto união de A e B, denotado por $ A\cup B $, tal que,
\begin{align*} A\cup B & = \{\omega \in \Omega: ~\omega \in A \textrm{ ou } \omega \in B\}. \end{align*}Exemplo
Sejam os conjuntos:
\begin{align*} A & =\{1,2,3\} \ \mbox{e} \ B=\{3,4,5,6\}, \end{align*}então
\begin{align*} A\cup B & =\{1,2,3,4,5,6\}. \end{align*}Interseção de dois eventos
Sejam A e B, dois eventos quaisquer de $ \Omega $, então o conjunto que contém todos os elementos que estão em A e B, é definido como a interseção de A e B, denotado por $ A\cap B $ ou $ AB $, tal que,
\begin{align*} A \cap B & = \{\omega \in \Omega: ~\omega \in A \textrm{ e } \omega \in B\}. \end{align*}- Do Exemplo sobre união de eventos, temos que a intersecção de $ AB = {3} $.
Eventos Disjuntos ou multuamente exclusivos
Sejam A e B, dois eventos quaisquer de $ \Omega $, então estes são disjuntos ou mutuamente exclusivos quando não existir elementos em comum entre A e B, isto é, $ A\cap B = \emptyset $.
Exemplo
Sejam os eventos $ A=\{1,2,3,4\} $ e $ B=\{5,6\} $, então $ A\cap B=\varnothing $.
Eventos equivalentes
Dois eventos $ A $ e $ B $ são definidos equivalentes, ou iguais, se $ A\subseteq B $ e $ B \subseteq A $.
Exemplo
Sejam os eventos $ A=\{1,2,3,4\} $ e $ B=\{5,6\} $, então $ A\cap B=\varnothing $.
Evento complementar
Seja $ A $ um evento de $ \Omega $. Então o complemento do evento A com respeito a $ \Omega $, denotado por $ \overline{A} $, $ A^c $, ou $ \Omega-A $, é o subconjunto dos elementos de $ \Omega $ exceto os elementos do evento A, isto é,
\begin{align*}\label{compeventos} A^c & = \{\omega \in \Omega: ~ \omega \notin A\}. \end{align*}Exemplo
Seja o espaço amostral $ \Omega $ do experimento que consiste em arremessar três moedas honestas. Diremos que $ H $ consiste na face superior da moeda ser cara, e $ T $ coroa. Assim,
\begin{align*} \Omega = &\{(H,H,H),(H,H,T),(H,T,H),(H,T,T),\\ & (T,H,H),(T,H,T),(T,T,H),(T,T,T)\}. \end{align*}e um subconjunto de $ \Omega $, cujo evento será aparecer cara na primeira moeda, dado por
$$ A=\{(H,H,H),(H,H,T),(H,T,H), (H,T,T)\}. $$Então o complemento de A será:
$$ \overline{A}=\{(T,H,H),(T,H,T), (T,T,H), (T,T,T)\}. $$Diferença de dois eventos
Sejam A e B dois eventos de $ \Omega $. O conjunto de todos os elementos de $ A $ que não estão em $ B $, serão denotados por $ A-B $ ou $ A\setminus B $, sendo definido por conjunto diferença, isto é,
\begin{align*} A - B & = \{\omega \in \Omega: ~\omega \in A \textrm{ e } \omega \notin B\}. \end{align*}Exemplo
Sejam os conjuntos $ A=\{1,2,3,4\} $ e $ B =\{3,4\} $, então $ A-B=\{1,2\} $.
Partição
Considerando uma sequência de eventos $ A_1 $, $ A_2 $, $ \ldots $, $ A_n $, não vazios, é uma partição do evento $ A $, se e somente se,
- $ A = \bigcup_{i = 1}^{n}A_i $;
- $ A_1 $, $ A_2 $, $ \ldots $, $ A_n $ são multuamente disjuntos, tais que $ A_i \cap A_j, ~\forall i \neq j $.
Leis na teoria de conjuntos
Considere três eventos $ A $, $ B $, e $ C $ definidos em $ \Omega $, então segue que:
- Lei comutativa: $ A\cup B = B \cup A$ e $A\cap B = B \cap A $;
- Lei associativa: $ A \cup (B\cup C)=(A\cup B)\cup C $;
- Lei distributiva: $ A \cup (B \cap C)=(A\cup B)\cap (A\cup C) $ e $ A \cap (B \cup C)=(A\cap B)\cup (A\cap C) $;
- Lei DeMorgan: $ (A \cup B)^c = A^c \cap B^c $ e $( A \cap B)^c = A^c \cup B^c $.
Ver livro EPAEC!.
Identidades em conjuntos
Sejam os eventos $ A $ e $ B $ definidos no espaço amostral $ \Omega $, não vazio. Então, apresentamos as seguintes identidades:
- $ A\cap A^c = \emptyset $;
- $ A \cup A^c = \Omega $;
- $ \Omega^c = \emptyset $;
- $ \emptyset^c = \Omega $;
- $ (A^C)^C=\overline{(\overline{A})}=A $, em outras palavras, o complemento de $ \overline{A} $ é igual a $ A $;
- $ A\Omega=A $ (Elemento neutro);
- $ A\cup \Omega=\Omega $;
- $ A \cap A = A $ (Idempotência);
- $ A\varnothing=\varnothing $ (Elemento absorvente);
- $ A\cup \varnothing = A $;
- $ A - B = A - (A \cap B) = A \cap B^c $;
\(B = (B \cap A) \cup (B \cap A^c)\);\(B - A = B \cap A^c\);\(A \cup B = A \cup (B \cap A^c)\);\(A \cup B = (A^c \cap B)\cup (A \cap B) \cup (A \cap B^c)\).
