Estatística e Probabilidade

Aula 12 - Probabilidades (Parte II)

Ben Dêivide | UFSJ
Estatística e Probabilidade

Selo DC

Motivação

Na Aula 02 vimos como uma das motivações...

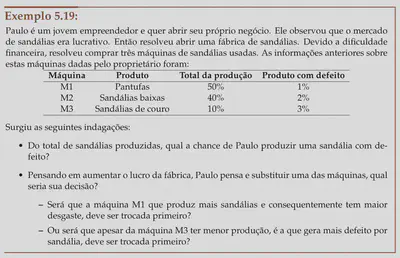
Motivação

  • Veremos que por meio de algumas propriedades da probabilidade, poderemos chegar a algumas soluções para esse problema

Definições de probabilidades

Lançar um dado equilibrado e observar o resultado obtido na face superior do dado.considerando que esse dado é equilibrado, e o evento $ A\subset \Omega $, então podemos calcular a chance de $ A $ ocorrer pela la medida de probabilidade, da seguinte forma:

\begin{align*} P(A) & = \frac{\#A}{6} = \frac{\textrm{número de resultados favoráveis a A}}{\textrm{número de resultados possíveis}}. \end{align*}

Essa é a conhecida a probabilidade clássica!

Evento aleatório

Todo evento de $ \Omega $ que podemos atribuir uma probabilidade, chamamos de evento aleatório.



Medida de probabilidade

Seja $ \Omega $ o espaço amostral, então uma função $ P $, tal que $ P:\Omega \to \mathbb{R} $, é chamada de medida de probabilidade ou probabilidade, aos eventos do espaço amostral satisfazendo os seguintes axiomas de Kolmogorov:

  1. $ P(\Omega) = 1 $;
  2. $ 0\leq P(A) \leq 1$, $ \forall \ A \subset \Omega $;
  3. $ P(A_1 \cup A_2) = P(A_1) + P(A_2)$, com $A_1 \cap A_2 = \emptyset $, para $ A_1, ~A_2 \subset \Omega $.

Exemplo

Uma peça moldada de injeção é igualmente provável de ser obtida, a partir de qualquer uma das oito cavidades de um molde.

  • Qual é o espaço amostral?
  • Qual é a probabilidade de a peça ser proveniente da cavidade 1 ou 2?
  • Qual é a probabilidade de a peça não ser proveniente nem da cavidade 3 nem da 4?

Nesse caso, (a) o espaço amostral é $ \Omega = \{1, 2, 3, 4, 5, 6, 7, 8\} $. Como a peça moldada de injeção é igualmente provável, então (b) a probabilidade de a peça ser proveniente da cavidade 1 ou 2, é dada por:

\[\begin{aligned} P(\{1\} \cup \{2\}) & = P(\{1\}) + P(\{2\}), \quad \textrm{(Eventos disjuntos)}\\ & = 1 / 8 + 1 / 8\\ & = 2 / 8. \end{aligned}\]

Exemplo (continuação…)

Por fim, (c) a probabilidade de a peça não ser proveniente nem da cavidade 3 nem da 4, é dada por:

\[\begin{aligned} P(\{3\}^c \cap \{4\}^c) & = P[(\{3\} \cup \{4\})^c], \quad \textrm{(Lei DeMorgan)}\\ & = 1 - P(\{3\} \cup \{4\}), \quad \textrm{(Evento complementar)}\\ & = 1 - [P(\{3\}) + P( \{4\})], \quad \textrm{(Eventos disjuntos)}\\ & = 1 - [1 / 8 + 1 /8]\\ & = 1 - 2 /8\\ & = 6 / 8. \end{aligned}\]

Propriedades da medida de probabilidade

Considere um espaço amostral e dois eventos não vazios $ A $ e $ B $, então a probabilidade de ocorrência do evento $ A $ ou do evento $ B $ é igual a: \[\begin{aligned} P(A\cup B) & = P(A)+P(B)-P(A\cap B). \end{aligned}\] Caso os eventos $ A $ e $ B $ sejam mutuamente exclusivos, isto é, $ P(A\cap B)=0 $, então: \[\begin{aligned} P(A\cup B) & = P(A)+P(B). \end{aligned}\] Essa regra pode ser estendida para $ n $ eventos mutuamente exclusivos: $ A_1 $, $ A_2 $, $ \ldots $, $ A_n $, isto é, \[\begin{aligned} P(A_1\cup A_2\cup \ldots \cup A_n)= P(A_1)+P(A_2)+\ldots+P(A_n). \end{aligned}\]

Exemplo

Uma empresa de eletricidade oferece uma taxa vitalícia de energia a qualquer lar cuja utilização de energia esteja abaixo de $ 240 $ kWh durante um determinado mês. Represente por $ A $ o evento de um lar selecionado aleatoriamente em um comunidade que não excede a utilização da taxa vitalícia em janeiro e por $ B $ o evento análogo para o mês de julho ($ A $ e $ B $ se referem ao mesmo lar). Suponha que $ P(A) = 0,8 $, $ P(B) = 0,7 $ e $ P(A \cup B) = 0,9 $. Calcule:

  1. $ P(A \cap B) $;
  2. A probabilidade de a quantia da taxa vitalícia ser excedida em exatamente um dos dois meses. Descreva esse evento em termos de $ A $ e $ B $.
Considere, \[\begin{aligned} A & = \{\omega \in \Omega: \omega = \textrm{``lar X que não excede 240kWh em janeiro''}\}, \\ B & = \{\omega \in \Omega: \omega = \textrm{``lar X que não excede 240kWh em julho''}\}.\\ \end{aligned}\] Então, para o primeiro ítem (a), temos que: \[\begin{aligned} P(A\cup B) & = P(A) + P(B) - P(A \cap B). \end{aligned}\]

Exemplo (continuação…)

Isso ocorre porque os eventos não são disjuntos, uma vez que os dois eventos consistem no mesmo lar X, em ser selecionado. Assim, podemos obter $ P(A \cap B) $, dado por: \[\begin{aligned} P(A\cap B) & = P(A) + P(B) - P(A \cup B) \\ & = 0,8 + 0,7 - 0,9 \\ & = 0,6. \end{aligned}\] No caso do ítem (b), o evento que representa o lar X de a quantia vitalícia ser excedida em exatamente um dos dois meses por ser representado por: $ (A^c \cap B) \cup (A \cap B^c) $, uma vez que,

\[\begin{aligned} A^c = \{\omega \in \Omega: \omega = \textrm{``lar X que exceder 240kWh em janeiro''}\}, \\ B^c = \{\omega \in \Omega: \omega = \textrm{``lar X que exceder 240kWh em julho''}\}.\\ \end{aligned}\]

Podemos ainda observar que $ A \cup B = (A^c \cap B)\cup (A \cap B) \cup (A \cap B^c) $, e que cada um dos eventos dentro do parêntese são disjuntos dois a dois, logo,

\[\begin{aligned} P(A \cup B) & = P[(A^c \cap B)\cup (A \cap B) \cup (A \cap B^c)]\\ & = P[(A^c \cap B) \cup (A \cap B^c)] + P(A \cap B). \end{aligned}\]

Exemplo (continuação… )

Desse modo, percebemos que $ P[(A^c \cap B) \cup (A \cap B^c)] = P(A \cup B) - P(A \cap B) $, logo, \[\begin{aligned} P[(A^c \cap B) \cup (A \cap B^c)] & = 0,9 - 0,6 = 0,3. \end{aligned}\]

Probabilidade de um evento complementar

Considere um espaço amostral e o evento, não vazio, $ A $, então a probabilidade do evento complementar $ A^c $ ocorrer, é dado por: \[\begin{aligned} P(A^C)=1-P(A). \end{aligned}\] Essa situação é consequência da regra da adição para $ A\subset\Omega $, e substituindo $ B $ por $ A^C $, temos \[\begin{aligned} P(A\cup A^C) & = P(A)+P(A^C)-P(A\cap A^C),\\ P(\Omega) & = P(A)+P(A^C)-0,\\ 1 & = P(A)+P(A^C), \end{aligned}\] logo segue a expressão anterior.

Exemplo

Usando os resultados do Exemplo anterior, podemos calcular a probabilidade de $ A^c $, como: \[\begin{aligned} P(A^c) & = 1 - 0,8 = 0,2. \end{aligned}\] Isso representa a chance do lar X exceder a energia acima de 240kWh, em janeiro.

Probabilidade condicional

Dados dois eventos $ A $ e $ B $ definidos em $ \Omega $, então a probabilidade condicional do evento $ A $ dado que ocorreu o evento $ B $, denotado por $ P(A|B) $, é definida por: \[\begin{aligned} P(A|B) = \frac{P(A \cap B)}{P(B)}, \end{aligned}\] para $ P(B) > 0 $.


Exemplo (Motivação)

Baseado no problema de Paulo, denotaremos os eventos:

  • evento $ D $ as sandálias produzidas com defeitos pela empresa;
  • $ M_1 $ o evento que representa as sandálias produzidas pela máquina $ M_1 $;
  • $ M_2 $ o evento que representa as sandálias produzidas pela máquina $ M_2 $, e;
  • $ M_3 $ o evento que representa as sandálias produzidas pela máquina $ M_3 $.

Desse modo podemos representar, a probabilidade desses defeitos da seguinte forma: $ P(D|M_1) = 0,01 $, $ P(D|M_2) = 0,02 $, e $ P(D|M_3) = 0,03 $. Assim, percebemos que a probabilidade do evento $ D $ não pode ser observada facilmente, pois o defeito dos produtos produzidos pelas máquinas está condicionado a cada máquina.

Regra do produto de probabilidade

Seja os eventos não vazios $ A_1,A_2,\ldots,A_n $ em $ \Omega $, com $ P(\bigcap^{n}_{i=1}A_i)>0 $, então a probabilidade do produto desses eventos é dado por $$ P(A_1\cap A_2\cap \ldots \cap A_n)=P(A_1)P(A_2|A_1)\ldots P(A_n|A_1\cap A_2 \cap \ldots \cap A_{n-1}). $$

Partição de $ \Omega $

Se a sequência $ A_1, A_2, \ldots, $ são disjuntos dois a dois, não vazios, e $ \bigcup^{\infty}_{i=1}A_i=\Omega $, então dizemos que essa sequência forma uma partição de $ \Omega $.


Teorema da probabilidade total

Seja uma sequência de eventos $ A_1, A_2, \ldots, A_n $ de $ \Omega $, disjuntos, tal que $ \bigcup^{n}_{i = 1}A_i = \Omega $, e $ B $ um evento de $ \Omega $, não vazio, então a probabilidade de $ B $ é dada por: \[\begin{aligned} P(B) = \sum_{i = 1}^{n}P(B|A_i)P(A_i), \end{aligned}\] para $ P(A_i) > 0 $, sendo $ i = 1, 2, \ldots, n $.

Exemplo (Motivação)

Voltando ao problema de Paulo, como $ P(M_1) = 0,50 $, $ P(M_2) = 0,40) $ e $ P(M_3) = 0,10 $, então a probabilidade de uma sandália ter defeito é \[\begin{aligned} P(D) = & \sum_{i = 1}^{3}P(D|M_i)P(M_i)\\ = & P(D|M_1)P(M_1) + P(D|M_2)P(M_2) + P(D|M_3)P(M_3)\\ = & 0,01 \times 0,50 + 0,02 \times 0,40 + 0,03 \times 0,10\\ = & 0,016. \end{aligned}\]

Independência de dois eventos

Considere o espaço amostral $ \Omega $. Dois eventos $ A $ e $ B $ de $ \Omega $ são independentes se satisfaz ao menos uma das seguintes condições:

  1. $ P(A \cap B) = P(A)P(B) $;
  2. $ P(A|B) = P(A) $, para $ P(B) > 0 $;
  3. $ P(B|A) = P(B) $, para $ P(A) > 0 $.


continuação…

É fácil mostrar que (I) implica em (II), (II) implica em (III), e (III) implica em (I).
  • $ (i) \to (ii) $: Se $ P(AB) = P(A)P(B) $, então:
$$ P(A|B) = \frac{P(AB)}{P(A)} = \frac{P(A)P(B)}{P(B)} = P(A), \quad \textrm{para } P(B) > 0; $$
  • $ (ii) \to (iii) $: Se $ P(A|B) = P(A) $, então:
$$ P(B|A) = \frac{P(BA)}{P(A)} = \frac{P(A|B)P(B)}{P(A)} = P(B), \quad \textrm{para } P(A) > 0; $$
  • $ (iii) \to (i) $: Se $ P(B|A) = P(B) $, então:
$$ P(AB) = P(B|A)P(A) = P(B)P(A), \textrm{para } P(A) > 0. $$

continuação…

A intuição para independência fica justificada pelo fato de que $ A $ é independente de $ B $ tanto na ocorrência quanto a não ocorrência de $ B $ e isso não muda em nada a probabilidade da ocorrência de $ A $, isto é, $ P(A|B) = P(A) $ e $ P(A|B^c) = P( A) $. Essas duas expressões significam que \[\begin{aligned} P(A\cap B) & = P(B)P(A|B) = P(B)P(A)\\ P(A\cap B^c) & = P(B^c)P(A|B^c) = P(B^c)P(A). \end{aligned}\]

Teorema de independência de dois eventos

Se A e B são eventos independentes, não vazio, definidos em $ \Omega $, então

  • $ A $ e $ B^c $ também são independentes;
  • $ A^c $ e $ B $ também são independentes;
  • $ A^c $ e $ B^c $ também são independentes.

Exemplo

Sejam os resultados possíveis de um dado honesto, cujo espaço amostral é $ \Omega = \{1, 2, 3, 4, 5, 6\} $. Considere um evento que representa o conjunto dos números ímpares desse espaço amostral, $ A = \{1, 3, 5\} $, e outro evento que consite nos múltiplos de 3, $ B = \{3, 6\} $. A probabilidade de $ A $ é $ P(A) = 1/2 $, a probabilidade de B é $ P(B) = 1/3 $, e a probabilidade da interseção entre A e B é $ P(A \cap B) = 1/6 $. Veja que dado que o evento B ocorra, ou não ocorra $ B^c = \{1, 2, 4, 5\} $, a probabilidade do evento A é a mesma, veja:

\begin{align*} P(A|B) & = \frac{1/6}{1/3} = 1/2\\ P(A|B^c) & = \frac{2/6}{4/6} = 1/2. \end{align*}

Que é o mesmo que entender que $ P(A) \times P(B) = 1/6 = P(A\cap B) $. Logo, $ A $ e $ B $ são eventos independentes.

Exemplo

Seja um experimento cujo objetivo é verificar a face superior de um tetraedro, isto é, $ \Omega = \{1, 2, 3, 4\} $. Sejam os eventos em $ \Omega $, $ A = \{1, 4\} $, $ B = \{2, 4\} $ e $ C = \{3, 4\} $. Considerando o tetraedro honesto e que cada valor é equiprovável, assim $ P(A) = P(B) = P(C) = 1/2 $. Observamos que estes eventos são independentes dois a dois, isto é, $ P(A\cap B) = 1/4 = P(A)P(B) $, $ P(A\cap C) = 1/4 = P(A)P(C) $ e $ P(B\cap C) = 1/4 = P(B)P(C) $. Porém, $ P(A\cap B \cap C) = 1/4 \neq P(A) P(B) P(C) $. Logo, os eventos A, B e C não são independentes três a três.

Independência de uma sequência de eventos

Considere o espaço amostral $ \Omega $. Uma sequência de eventos $ A_1, A_2, \ldots, A_n $ de $ \Omega $ são independentes se e somente se:

\begin{align*} P(A_i \cap A_j) & = P(A_i)P(A_j), \quad \textrm{para } i \neq j; \\ P(A_i \cap A_j \cap A_k) & = P(A_i)P(A_j)P(A_k), \quad \textrm{para } i \neq j \neq k; \\ \vdots & \nonumber\\ P(\cap_{i = 1}^{n} A_i) & = \prod_{i = 1}^{n}P(A_i). \end{align*}

Exemplo (Motivação)

Paulo poderia indagar, se os eventos $ M_i $ e $ D $ são independentes ou dependentes. Contudo, pela Definição de independência, temos que

\begin{align*} P(D|M_i) & \neq P(D) = 0,016 \Rightarrow D \textrm{ e } M_i \textrm{, para } i = 1, 2, 3, \end{align*}

logo, não são independentes.

Teorema de Bayes

Considere o espaço amostral $ \Omega $. Considere uma sequência de eventos $ A_1, A_2, \ldots, A_n $ de $ \Omega $, disjuntos, tal que $ \bigcup^{n}_{i = 1}A_i = \Omega $, e $ B $ um evento de $ \Omega $, então a probabilidade de $ A_k $, para $ k = 1, 2, \ldots, n $, dado que ocorreu o evento $ B $, denotado por $ P(A_k|B) $, é dado por:

\begin{aligned} P(A_k|B) = \frac{P(B|A_k)P(A_k)}{\sum_{i = 1}^{n}P(B|A_i)P(A_i)}, \qquad k = 1, 2, \ldots, n, \end{aligned}

para $ P(A_k) > 0 $ e $ P(A_i) > 0 $, sendo $ i = 1, 2, \ldots, n $.

Exemplo (Motivação)

Com esse resultado, Paulo agora pode tomar uma decisão mais plausível, isto é, dado um defeito numa determinada sandália produzida na fábrica, qual a probabilidade desta ter sido produzida em cada uma das máquinas?

\begin{aligned} P(M_1|D) = \frac{0,01 \times 0,50}{0,016} = 0,3125\\ P(M_2|D) = \frac{0,02 \times 0,40}{0,016} = 0,5000\\ P(M_3|D) = \frac{0,03 \times 0,10}{0,016} = 0,1875\\ \end{aligned}

A tomada de decisão será substituir a máquina $ M_2 $. Poderíamos ter tomado uma decisão equivocada se não fosse o teorema de Bayes.

Questões?

Dúvidas e Sugestões

Contato