flowchart TD
B["Natureza das variáveis"]
B-->C("Variáveis qualitativas")
B-->D("Variáveis quantitativas")
C-->E{{"Nominal"}}
C-->G{{"Ordinal"}}
D-->H{{"Discreta"}}
D-->I{{"Contínua"}}
1 Definições gerais da estatística
1.1 Introdução
A estatística é uma ciência que estuda a coleta, organização, análise e registro de dados, sendo necessária tanto em nossa vida pessoal quanto em diversos ramos da sociedade. Isso porque essa área do conhecimento é capaz de fornecer informações que irão influenciar nossas decisões a serem tomadas através dos dados a serem utilizados para analisar fenômenos do passado norteando-nos possíveis situações que poderão ocorrer no futuro.
Na sessão a seguir, trabalharemos as definições gerais da Estatística, onde serão definidos os conceitos de população e amostra. Para iniciar o estudo da Estatística precisamos compreender alguns conceitos. Um deles é a ideia de população, Definição 1.1.
Definição 1.1 (População) A População é definida como um grupo ou conjunto de elementos que serão o objeto de estudo de uma pesquisa. O número de elementos é denotado por “\(N\)”.
No entanto, quando pensamos em população, logo vem à mente um conjunto de pessoas com características em comum, seja pessoas que moram em uma mesma cidade, bairro, comunidade rural, etc. Para ilustrar, vejamos o Exemplo 1.1.
Exemplo 1.1 Vamos pensar numa sala de aula. Supomos que um pesquisador fará um estudo sobre as características dos alunos do 3º ano do ensino médio de uma escola estadual e que deseja saber como é o desempenho da turma diante da disciplina de Matemática. O conjunto de alunos dessa referida classe no ano considerado é a população que será estudada. Algumas informações poderão fazer parte do estudo, como, por exemplo, o sexo (masculino ou feminino), idade, ou classe social (classes baixa, média ou alta) a que está inserida. Podemos representar essas informações por meio de gráficos, como exemplo, usamos um gráfico de pizzas para representar a característica dos alunos do 3º ano em relação ao seu sexo, Figura 1.1.
Uma população pode ser subdividida quanto ao número de elementos que a compõe, definida a seguir.
Definição 1.2 (População finita e infinita) Uma população é classificada finita quando o conjunto de elementos que a compões é limitado. Ao passo que uma população é infinita quando não há possibilidades de mensurar a quantidade de elementos que a compõe.
Os funcionários de uma papelaria, o número de vendas de picolés de uma sorveteria, as agências dos Correios de uma região de uma cidade, são ilustrações de populações finitas. Nesses casos, percebe-se que o número de elementos que compõe esse tipo de população é pequeno. Já a concentração de poluentes em um rio, leituras de sensores de uma máquina industrial, o número de estrelas em uma galáxia ou os pontos de uma reta, constituem populações infinitas.
Ao pensarmos na relação tempo e custo de uma pesquisa, muitas das vezes torna-se oneroso trabalhar com uma população inteira, em função do número de dias, meses ou anos, bem como do dinheiro envolvido para a realização da coleta de dados. Uma outra possibilidade da inviabilidade é não ter acesso a todos os elementos da população que se deseja estudar. Em função disso, trabalhamos com um subgrupo representativo dessa população, a qual denominamos de amostra.
Definição 1.3 (Amostra) Uma amostra é um subconjunto da população que é o objeto de análise da pesquisa. O número de elementos de uma amostra é “\(n\)”.
Em termos mais simples, podemos dizer que a amostra é uma parte que irá representar a população que desejamos realizar a pesquisa, conforme a Figura 1.2.
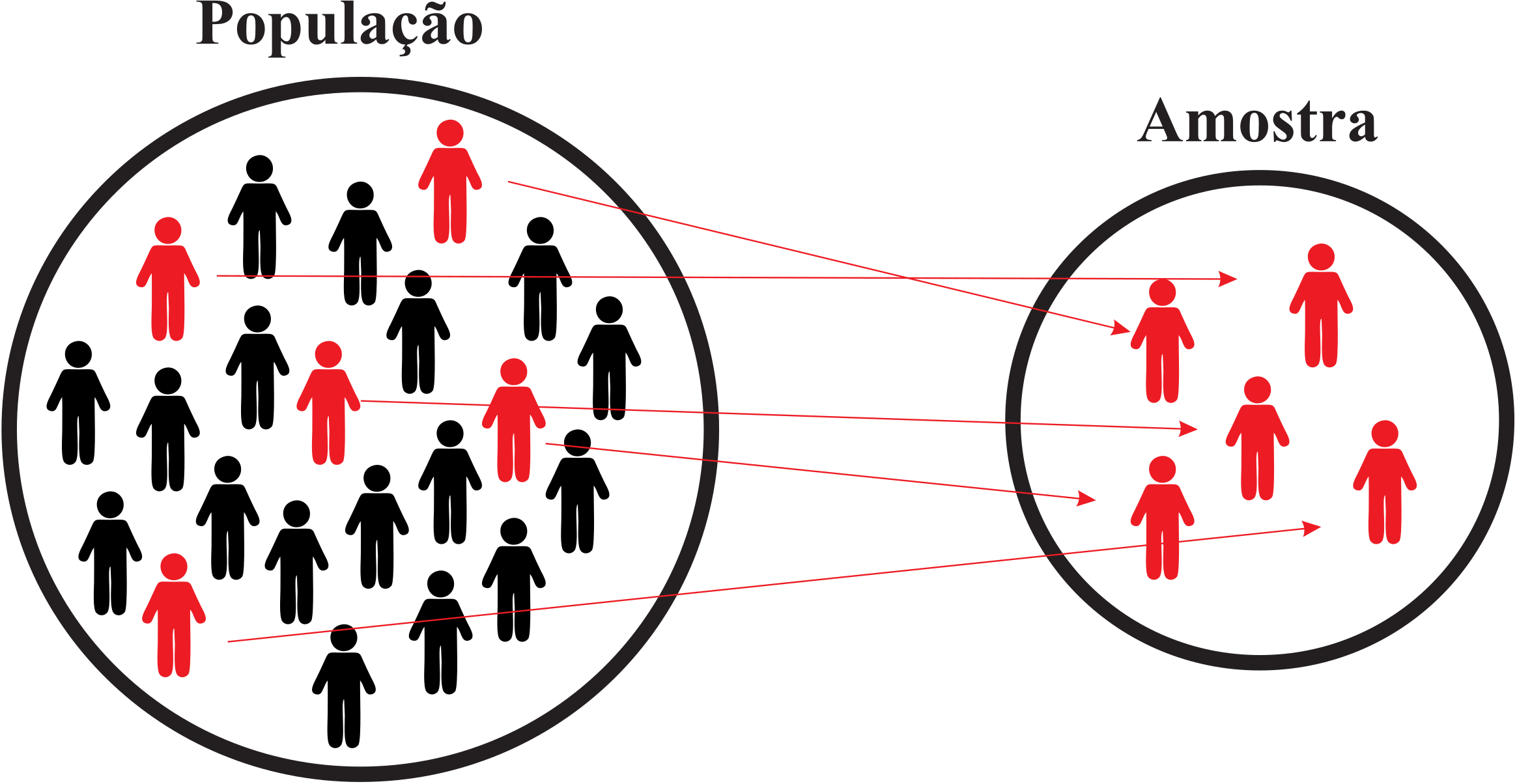
Vejamos o Exemplo 1.2 de amostra em uma pesquisa.
Exemplo 1.2 Vamos considerar uma fábrica de peças automotivas. Nessa fábrica existem três linhas de produção – cinto de segurança, freio de mão e pedal. Não é possível, pelo tempo e pelo custo, fazer uma inspeção em todas as três linhas de produção, mas é possível verificar a qualidade e assertividade do trabalho recolhendo-se amostras, em três momentos distintos da fabricação - início, meio e fim. A amostra é um importante recurso, pois traz essa vantagem da economia de tempo e rapidez, mas pode ocorrer alguma falha, quando não mostrar algum objeto defeituoso, que por ventura, possa não aparecer.
Alguns exemplos da influência da estatística no nosso cotidiano são as previsões climáticas, os índices de aumento ou queda de desemprego, as pesquisas de âmbitos eleitorais, as pesquisas de satisfação de clientes, os indicadores de negócios, entre diversos outros. É difícil pensar em uma área onde as técnicas estatísticas não possam ser aplicadas. Entretanto, seus resultados também estão associados a pequenas incertezas, pois são baseados em uma amostra e podem conter uma pequena margem de erro, assunto esse que será tratado na próxima sessão.
1.2 Definições gerais
Dentre as definições gerais da Estatística, destacamos: Estatística Descritiva, a Estatística Inferencial e a Probabilidade na estatística.
1.2.1 Estatística Descritiva
A Estatística Descritiva ou Estatística Dedutiva tem por objetivo a apresentação das principais características de um conjunto de dados que serão representados por meio de tabelas, gráficos e números. Ou seja, visa proporcionar medidas que sintetizem as informações dos dados coletados que são os valores observados da pesquisa, a fim de torná-las menos complexas e melhor compreendidas.
1.2.2 Estatística Inferencial ou Estatística Indutiva
A Estatística Inferencial consiste em analisar uma amostra (que é a redução da população em uma dimensão menor) a fim de expandir as informações contidas nessa amostra à toda a população - que é o objeto de investigação. Um exemplo seria o interesse de um sorveteiro em saber se seu sorvete está apto para comercialização antes de colocá-lo à venda, então ele degusta uma pequena porção para ter uma referência de como está o lote inteiro do sorvete.
Podemos compreender melhor o que seria amostra e população da seguinte maneira: a população da pesquisa corresponde ao lote inteiro do sorvete e a amostra como a parte que foi retirada para a degustação.
Assim, para que tenhamos o entendimento das informações contidas na amostra da população, é necessário a utilização de técnicas específicas da estatística a fim de que essas informações sejam as mais confiáveis possíveis. Nesse sentido, a inferência estatística deve se preocupar com o grau de incerteza dessas generalizações da população e para isso conta a probabilidade como suporte.
1.2.3 Probabilidade
A probabilidade é uma teoria importante na matemática, ela estuda a incerteza dos fenômenos aleatórios, tendo em vista que engloba as possibilidades de situações ocorrerem ou não. Essas chances são medidas a partir da razão do número de chances favoráveis pelo total dos casos possíveis. Desta forma, a probabilidade de um evento \(A\) ocorrer, pode ser definida pela seguinte fórmula:
\[ P(A) = \frac{\textrm{número de chances favoráveis ao evento A}}{\textrm{total de casos possíveis}}. \]
No nosso dia-a-dia a probabilidade atua de forma bem positiva, auxiliando em decisões importantes, como na vida financeira de uma empresa, através dos cálculos de lucro ou prejuízos, bem como nos cálculos das chances de um time ganhar um jogo em um campeonato de futebol.
Nos últimos dois anos, a probabilidade foi muito utilizada na condução dos procedimentos referentes à pandemia pela Covid-19, quando a OMS – Organização Mundial de Saúde – levou em conta evidências da relação de contato de pessoas com máscara e sem máscara, contaminação de pessoas quando estão em lugares abertos e fechados e até mesmo a relação da imunização com as vacinas e a proteção vacinal após a imunização, em comparação a não vacinados.
Por fim, será por meio da probabilidade que a estatística inferencial irá ser desenvolvida para o embasamento teórico das metodologias criadas para extrapolar as informações amostrais à população.
A seguir, trataremos das variáveis de interesse para estudo de uma população.
1.3 Tipos de variáveis
As variáveis de uma pesquisa são informações das características que são coletadas dentro do processo da Amostragem, que irão auxiliar na compreensão da população que está sendo amostrada.
Definição 1.4 (Variável) Uma variável representa a característica dos elementos da população da pesquisa, do qual se deseja estudar. Usamos letras maiúsculas: \(X\), \(Y\), \(W\), …, para representar as variáveis de interesse. O resultado observado das variáveis aos elementos, representam as realizações ou valores observados, e denotamos por letras minúsculas: \(x\), \(y\), \(w\), etc..
Dessa forma, cada característica coletada, como idade, sexo, peso e altura corresponde a uma variável. Quanto a sua natureza, ela é classificada em qualitativa ou quantitativa, descritos a seguir.
1.3.1 Variáveis qualitativas e quantitativas
As variáveis podem ser divididas em quantitativas – discreta ou contínua ou qualitativas – nominal ou ordinal, conforme ilustra a Figura 1.3.