6  Distribuições de probabilidades

Exercícios propostos

Exercício 6.1
Defina variável aleatória (V.A.), variável aleatória discreta (V.A.D.), variável aleatória contínua (V.A.C.) e descreva diversos exemplos na sua área de estudo.

Solução
Verifique a Definição 5.22 e formule sua resposta.

Exercício 6.2
Suponha que 2% dos itens produzidos por uma fábrica sejam defeituosos. Encontre a probabilidade P de existirem 3 defeituosos em uma amostra de 100.

Solução
Distribuição Binomial: \[\begin{align*} P(X = x) & = \binom{n}{x}p^x(1 - p)^{n - x}. \end{align*}\] Considerando \(p = 0,02\) e \(n = 100\), então \[\begin{align*} P(X = 3) & = \binom{100}{3}(0,02)^3(1 - 0,02)^{100 - 3}\\ & = 0,1823. \end{align*}\]

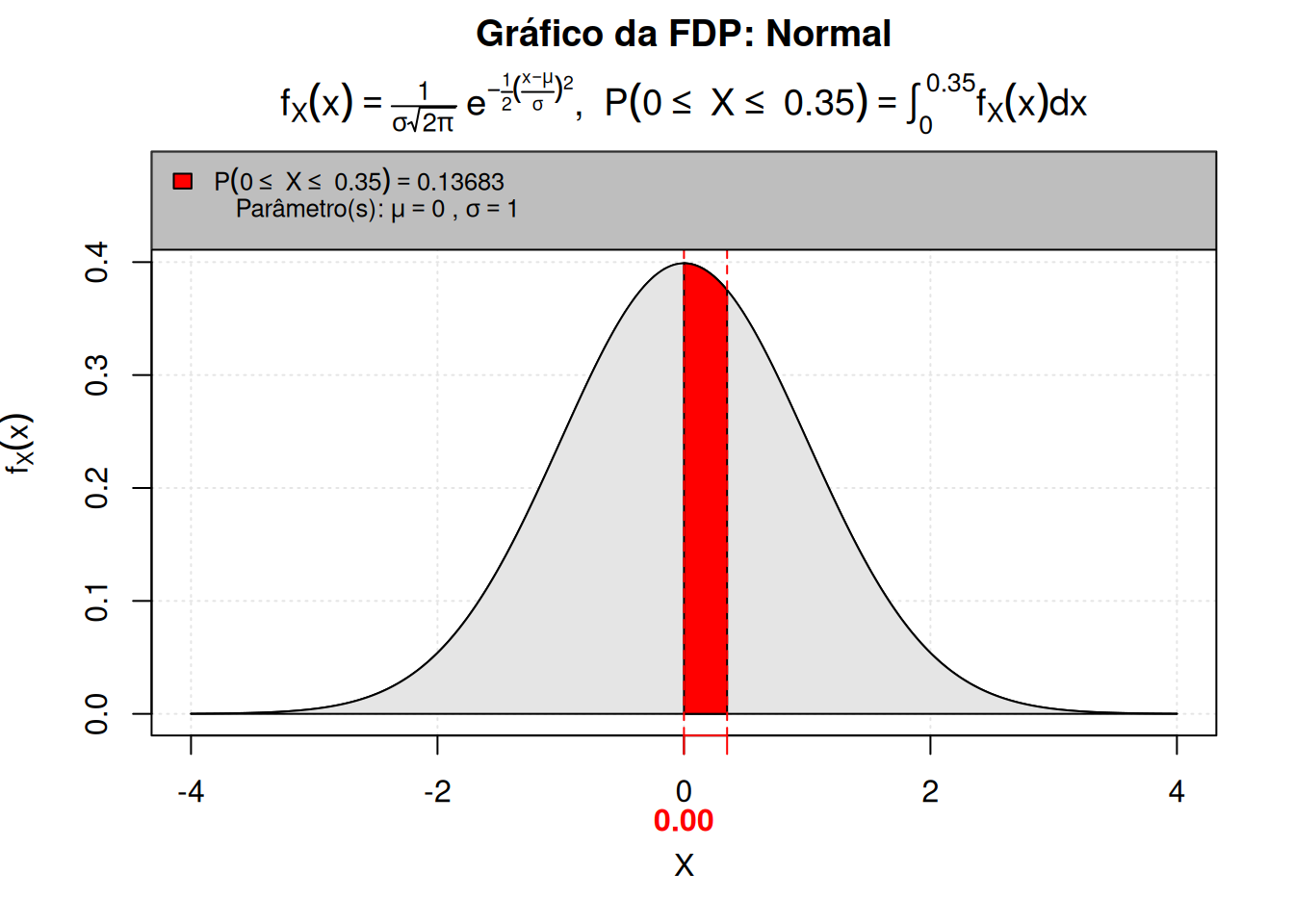
Exercício 6.3

Usando a curva normal padronizada, determinar as áreas subtendidas entre os valores abaixo, com representação gráfica.

  1. 0,35 e 0,0;
  2. 0,0 e 1,52;
  3. -0,34 e 1,9;
  4. à direita de -1,91;
  5. à esquerda de 1,13;
  6. à esquerda de -2,13.
Solução
  1. \(P(0,00 \leq Z \leq 0,35) = 0,1368\). Graficamente, podemos apresentar o cômputo dessa probabilidade usando Código R 6.1.
Código R 6.1: Probabilidade distribuição normal padrão. 
# Anexando leem
library(leem)
# Probabilidade P(0,00 \leq Z \leq 0,35)
P(0 %<=X<=% 0.35, mean = 0, sd = 1)

[1] 0.13683

Podemos representar este cálculo usando a Tabela da normal padrão, usando o Código R 6.2.

Código R 6.2: Probabilidade distribuição normal padrão. 
# Anexando leem
library(leem)
# Tabela
showtabnormal(0.35)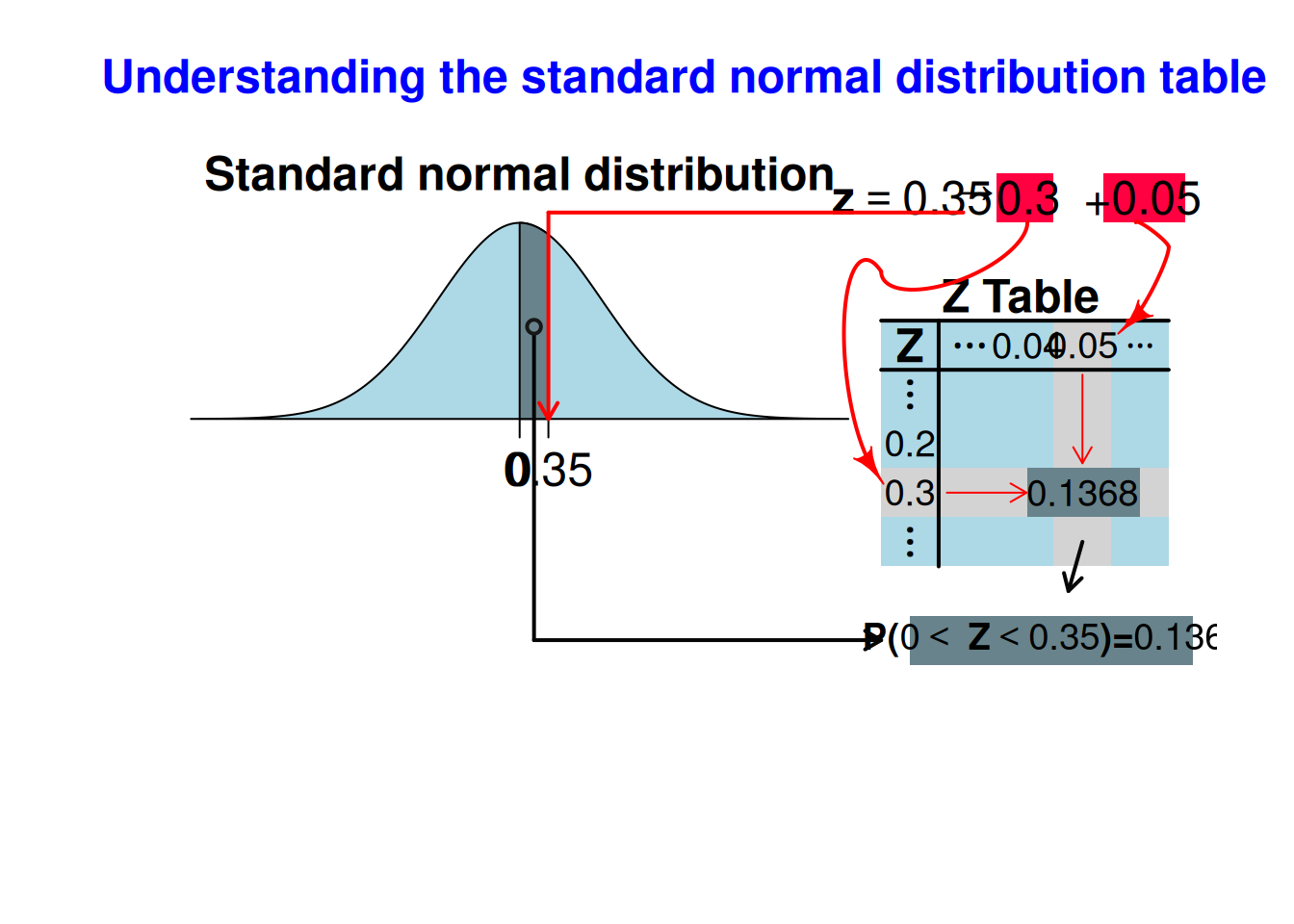

  1. \(P(0,00 \leq Z \leq 1,52) =0,4357\). Graficamente, podemos apresentar o cômputo dessa probabilidade usando Código R 6.3.
Código R 6.3: Probabilidade distribuição normal padrão. 
# Anexando leem
library(leem)
# Probabilidade P(0,00 \leq Z \leq 1,52)
P(0 %<=X<=% 1.52, mean = 0, sd = 1)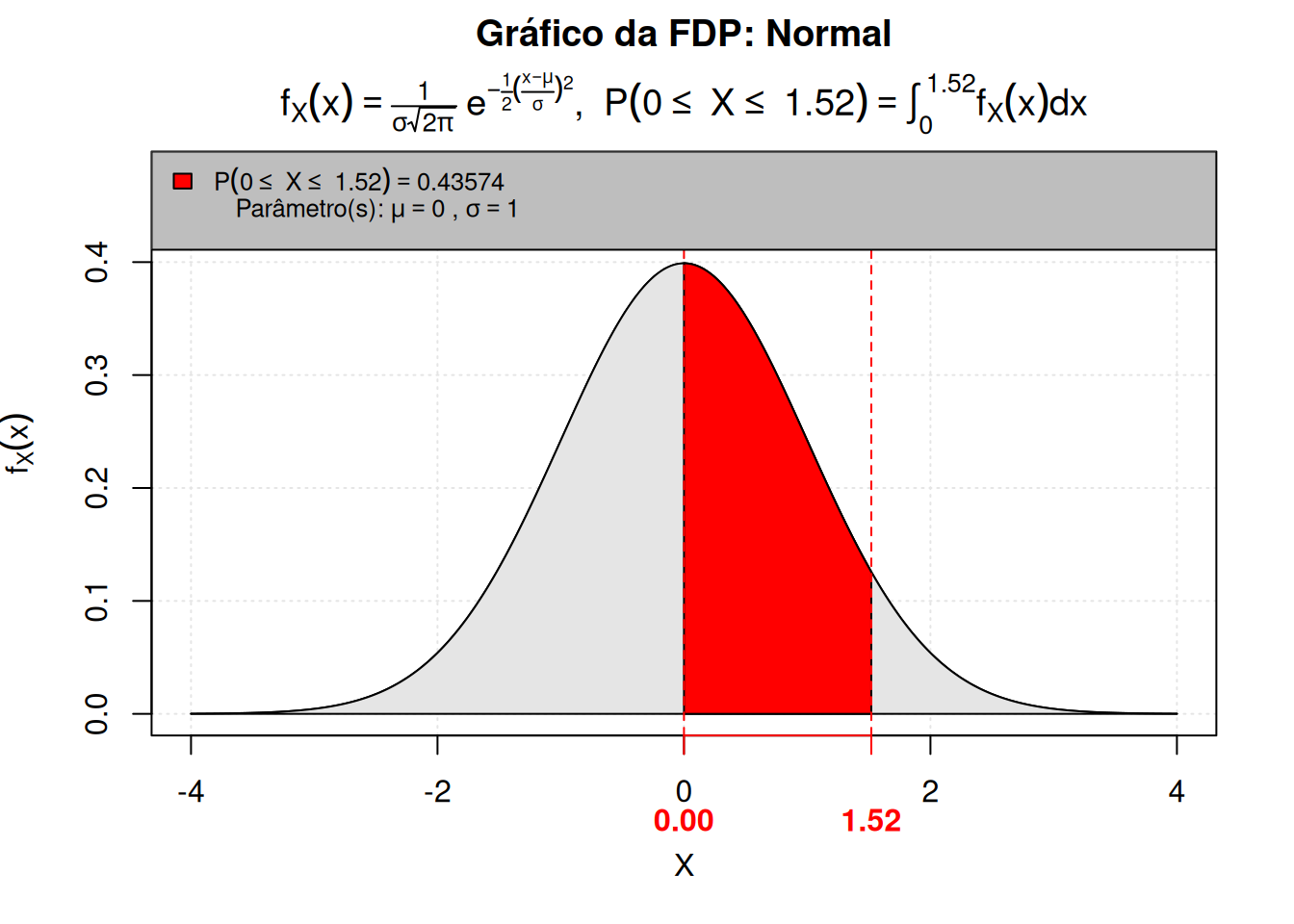

[1] 0.43574

Podemos representar este cálculo usando a Tabela da normal padrão, usando o Código R 6.4.

Código R 6.4: Probabilidade distribuição normal padrão. 
# Anexando leem
library(leem)
# Tabela
showtabnormal(1.52)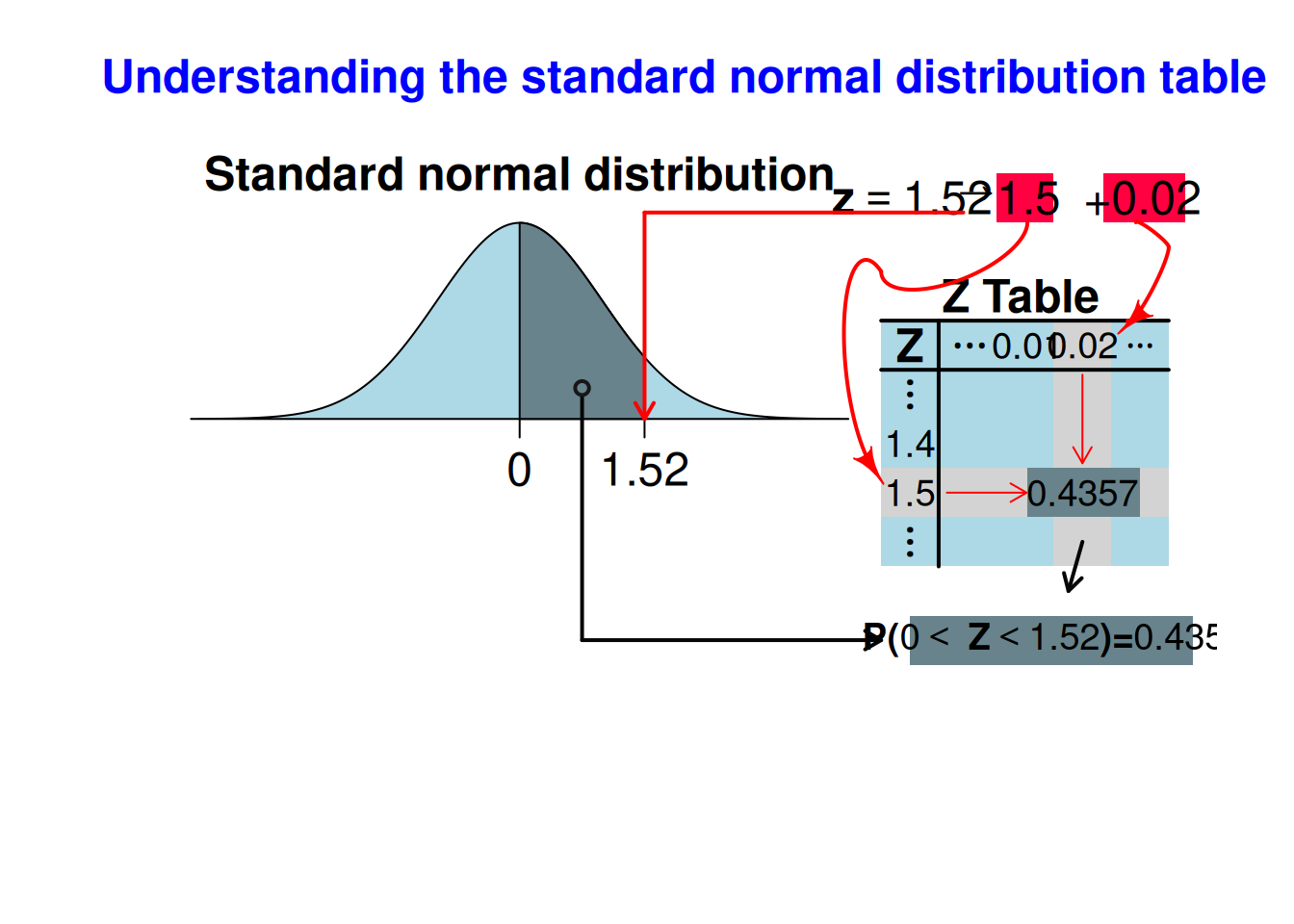

  1. \(P(Z \geq -1,91) = 0,4719\). Graficamente, podemos apresentar o cômputo dessa probabilidade usando Código R 6.5.
Código R 6.5: Probabilidade distribuição normal padrão. 
# Anexando leem
library(leem)
# Probabilidade P(Z \geq -1,91)
P(-1.97, mean = 0, sd = 1, lower.tail = F)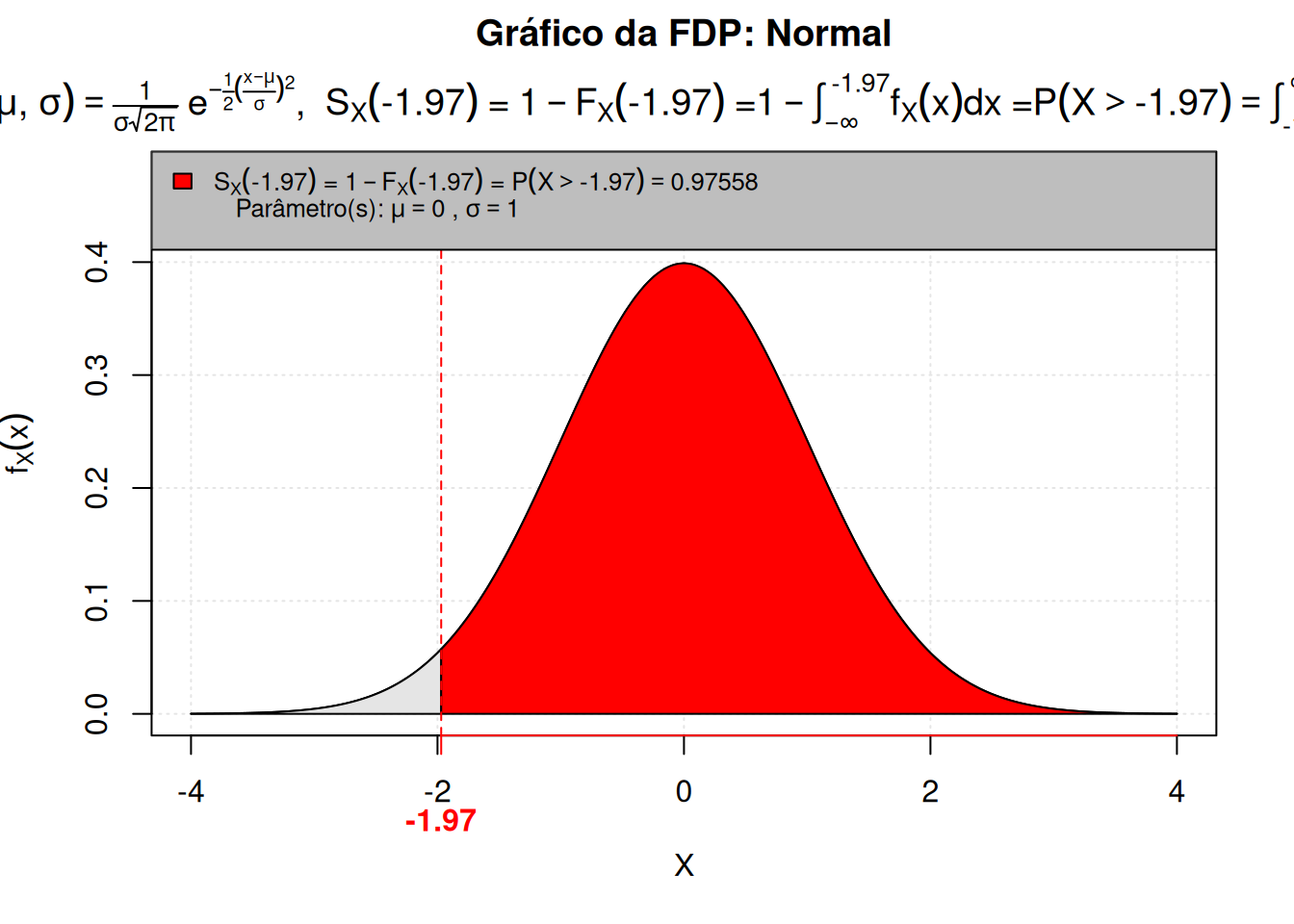

[1] 0.97558

Podemos representar este cálculo usando a Tabela da normal padrão, usando o Código R 6.6.

Código R 6.6: Probabilidade distribuição normal padrão. 
# Anexando leem
library(leem)
# Tabela
showtabnormal(1.97)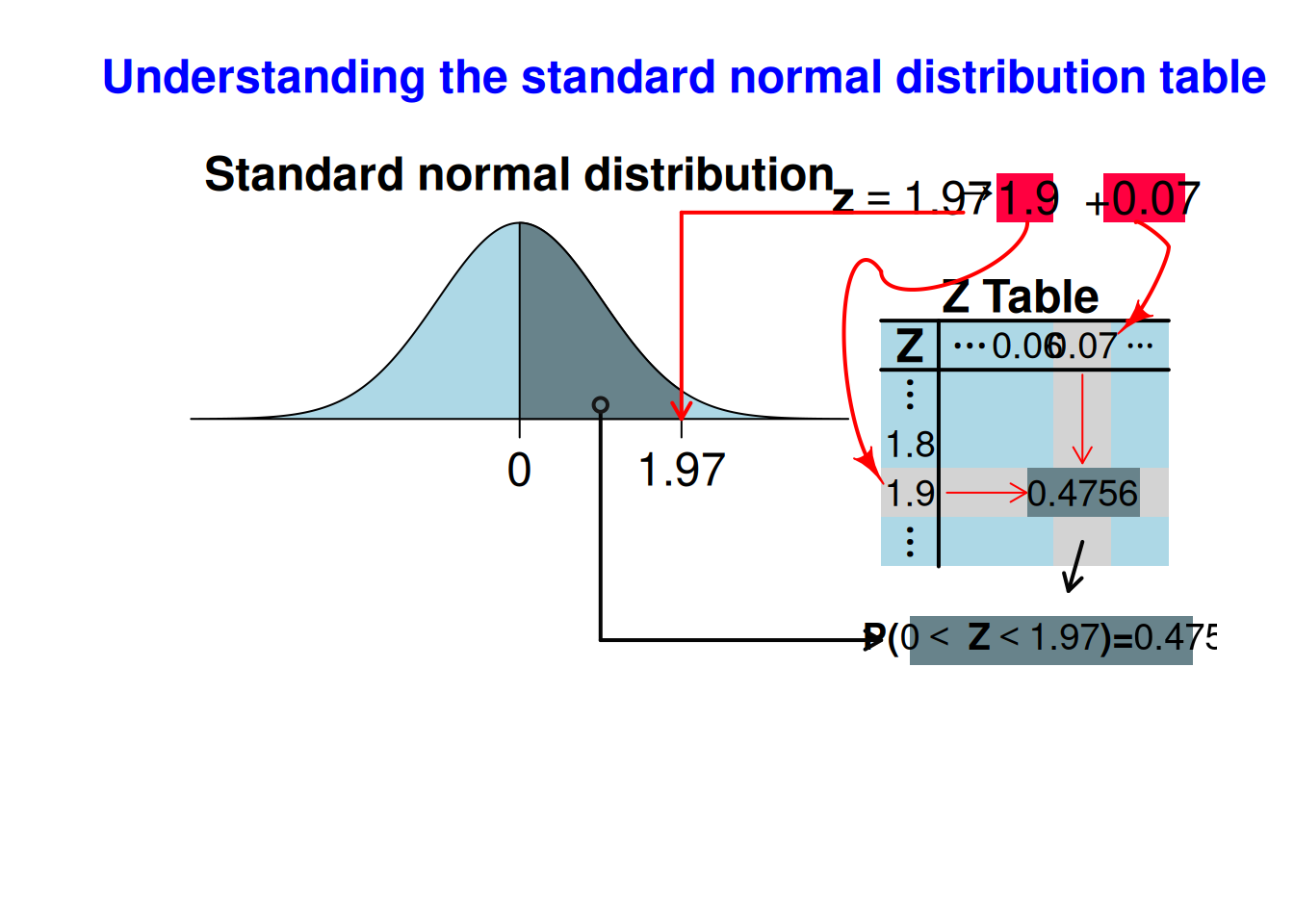

  1. \(P(Z \leq 1,13) = 0,5000 + 0,3708 = 0,8708\). Graficamente, podemos apresentar o cômputo dessa probabilidade usando Código R 6.7.
Código R 6.7: Probabilidade distribuição normal padrão. 
# Anexando leem
library(leem)
# Probabilidade P(Z \leq 1,13)
P(1.13, mean = 0, sd = 1)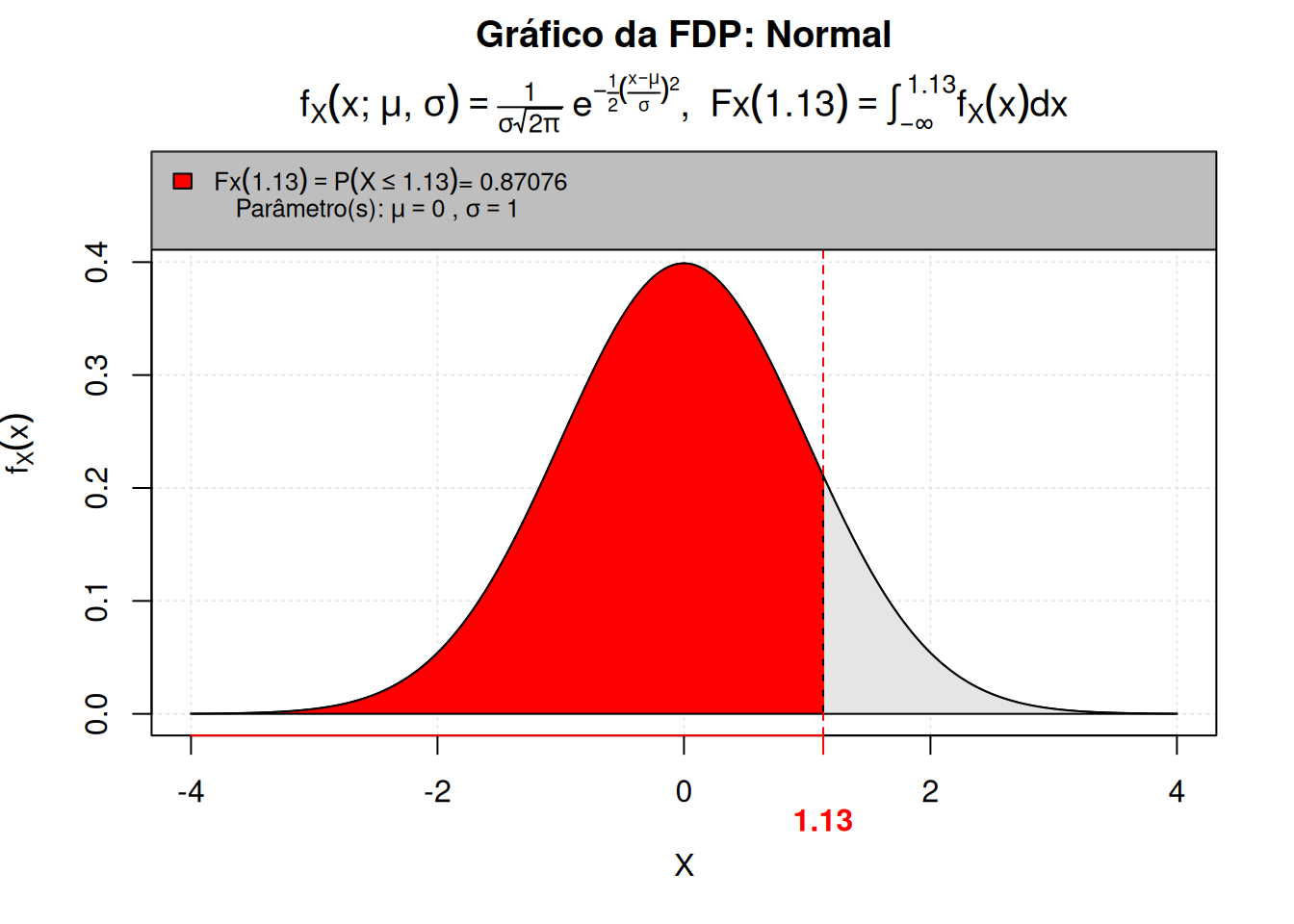

[1] 0.87076

Podemos representar este cálculo usando a Tabela da normal padrão, usando o Código R 6.10.

Código R 6.8: Probabilidade distribuição normal padrão. 
# Anexando leem
library(leem)
# Tabela
showtabnormal(1.13)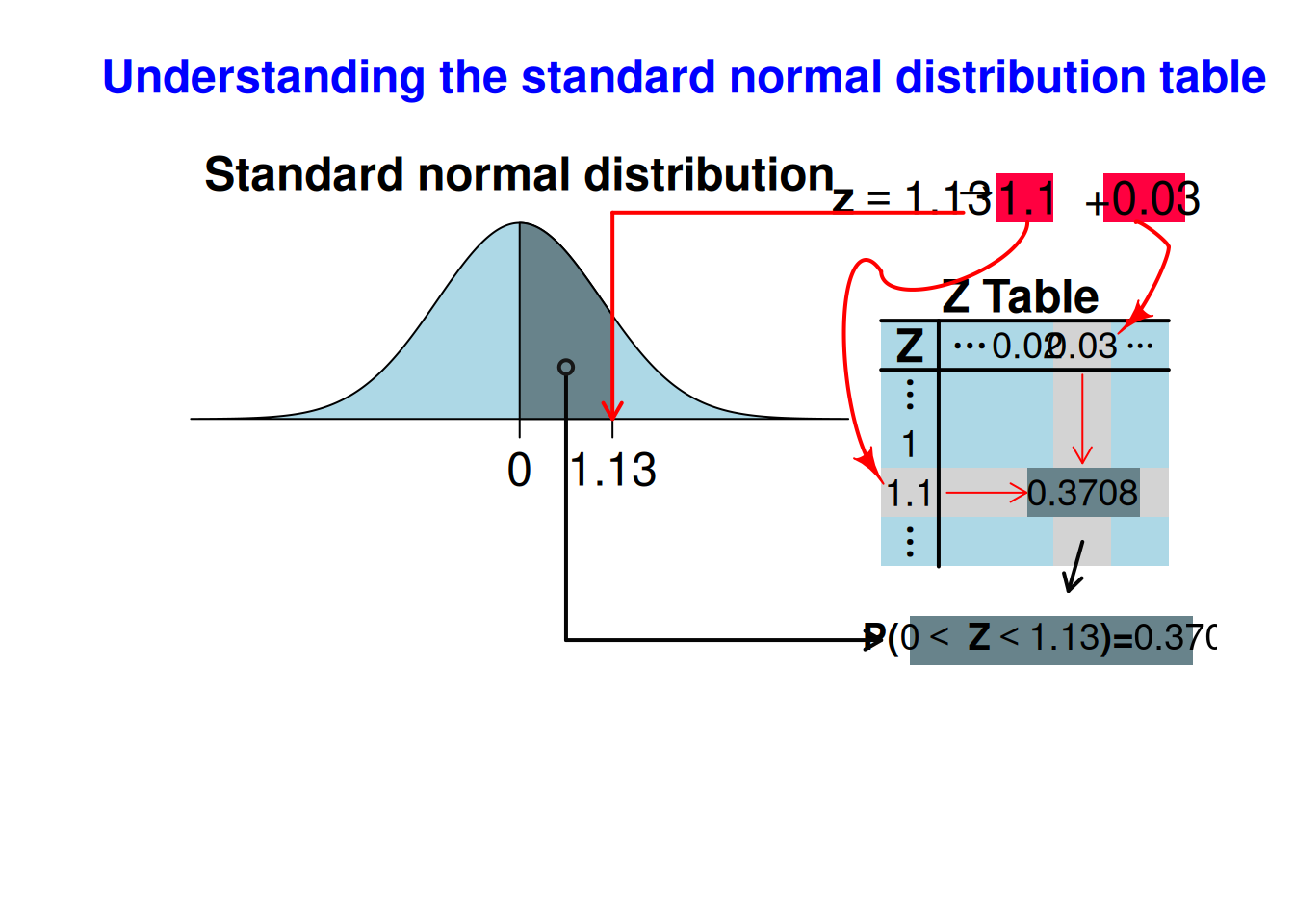

e) \(P(Z \leq -2,13) = 0,5000 - 0,4834 = 0,0166\). Graficamente, podemos apresentar o cômputo dessa probabilidade usando Código R 6.9.

Código R 6.9: Probabilidade distribuição normal padrão. 
# Anexando leem
library(leem)
# Probabilidade P(Z \leq -2,13)
P(-2.13, mean = 0, sd = 1)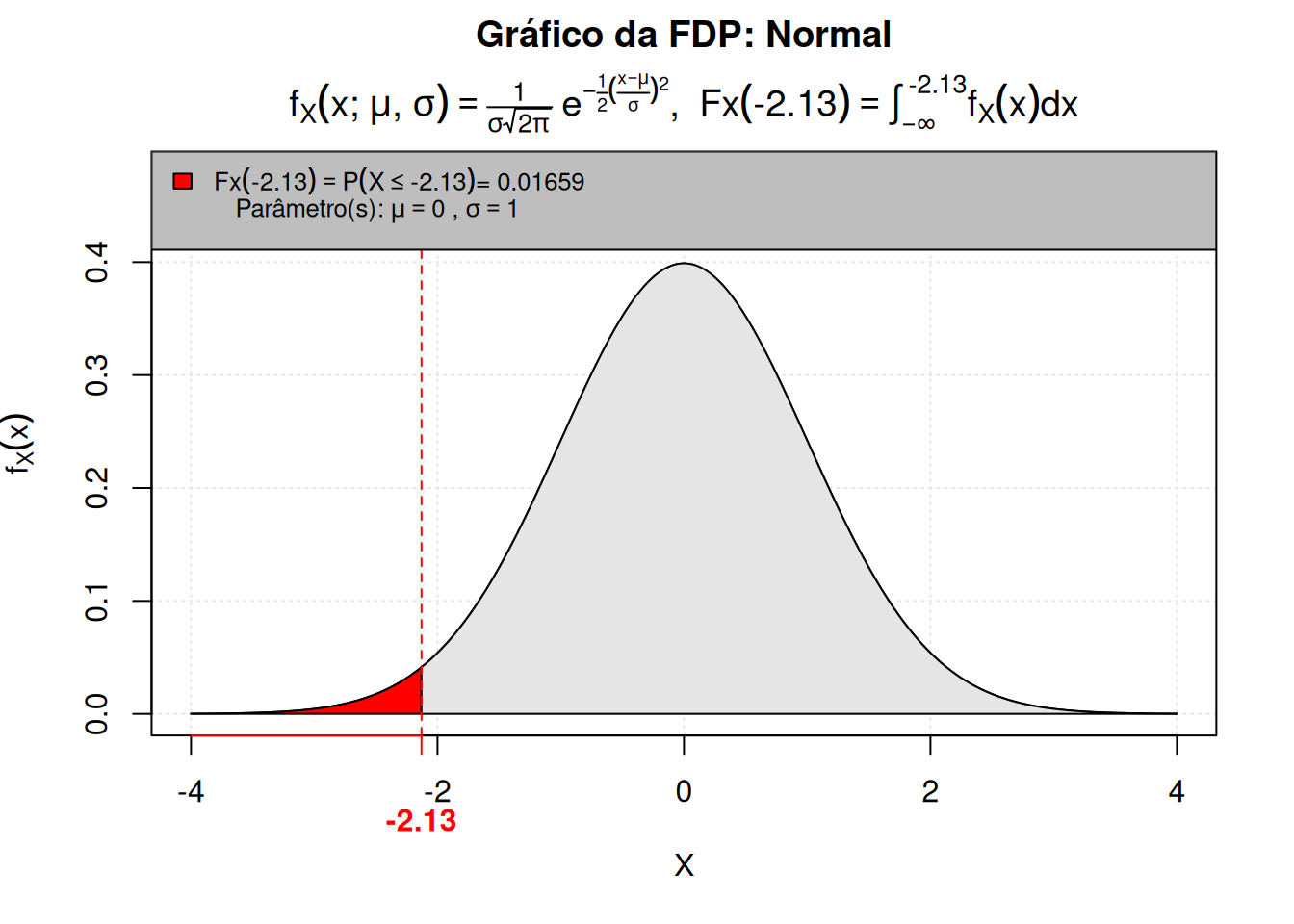

[1] 0.01659

Podemos representar este cálculo usando a Tabela da normal padrão, usando o Código R 6.10.

Código R 6.10: Probabilidade distribuição normal padrão. 
# Anexando leem
library(leem)
# Tabela
showtabnormal(2.13)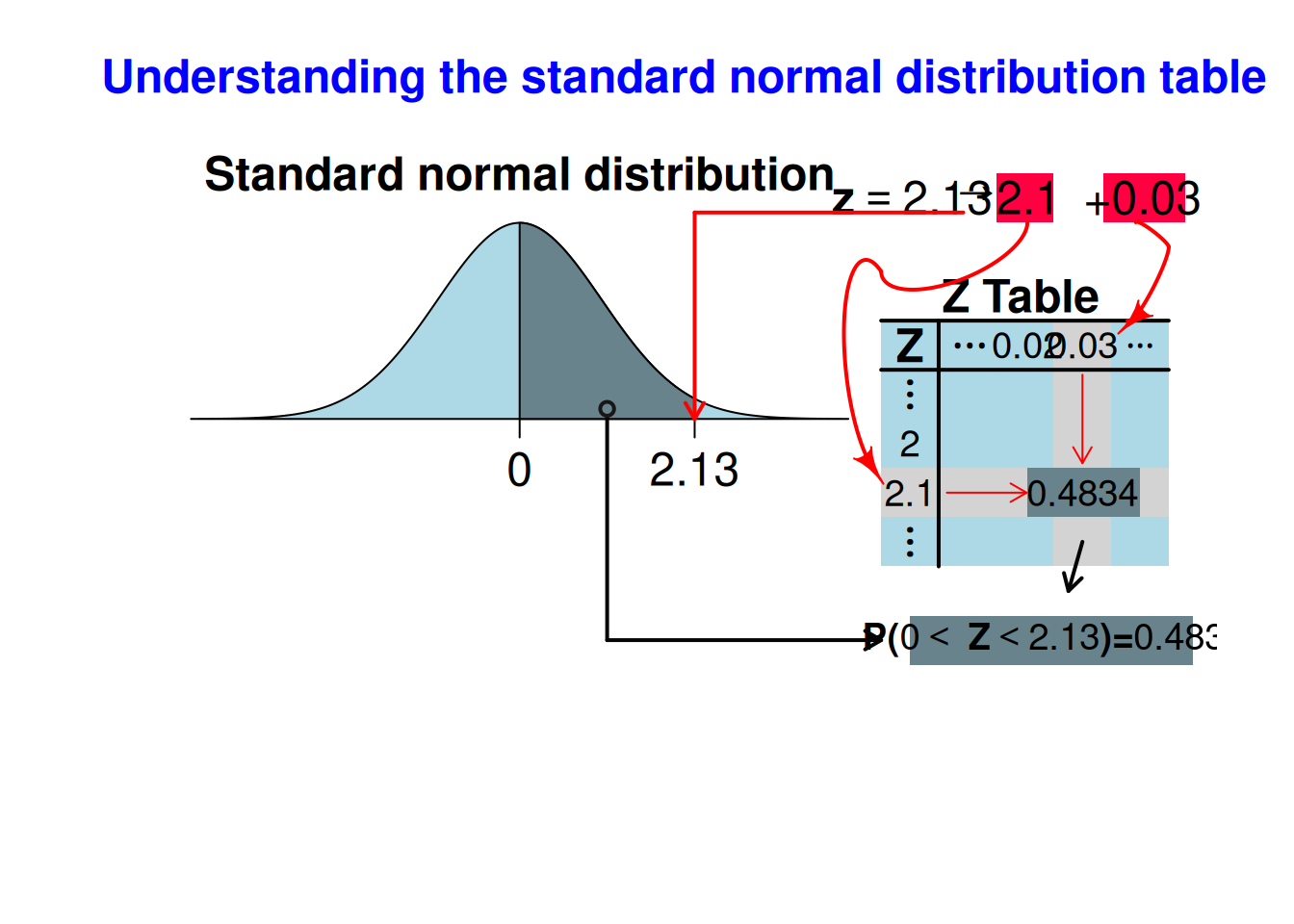

Exercício 6.4

Dada uma distribuição normal com \(\mu= 40\) e \(\sigma = 6\), calcular:

  1. \(P(X\leq 33)\);
  2. \(P(X \geq 29)\);
  3. \(P(39 \leq X \leq 45)\);
  4. Ponto que tem 58% de área acima dele;
  5. Ponto que tem 5% de área acima;
  6. \(P(Z > 0)\).
Solução

  1. Fazendo a transformação \(Z = \frac{X - \mu}{\sigma} = \frac{33 - 40}{6} = -1,17\), temos que \[\begin{align*} P(X\leq 33) & = P(Z \leq -1,17) \\ & = 0,5000 - P(-1,17 \leq Z \leq 0) \\ & = 0,5000 - 0,3790\\ & = 0,1210. \end{align*}\]

  2. Fazendo a transformação \(Z = \frac{X - \mu}{\sigma} = \frac{29 - 40}{6} = -1,83\), temos que \[\begin{align*} P(X\geq 29) & = P(Z \geq -1,83)\\ & = P(-1,83 \leq Z \leq 0) + 0,5000\\ & = 0,4664 + 0,5000 \\ & = 0,9664. \end{align*}\]

  3. Fazendo a transformação \(Z = \frac{X - \mu}{\sigma} = \frac{29 - 40}{6} = -1,83\), temos que \[\begin{align*} P(X\geq 29) & = P(Z \geq -1,83)\\ & = P(-1,83 \leq Z \leq 0) + 0,5000\\ & = 0,4664 + 0,5000\\ & = 0,9664. \end{align*}\]

  4. Para verificarmos o ponto que tem 58% de área acima dele, recorremos a função R Q(), isto é,

Q(0.58, mean = 0, sd = 1, lower.tail = F)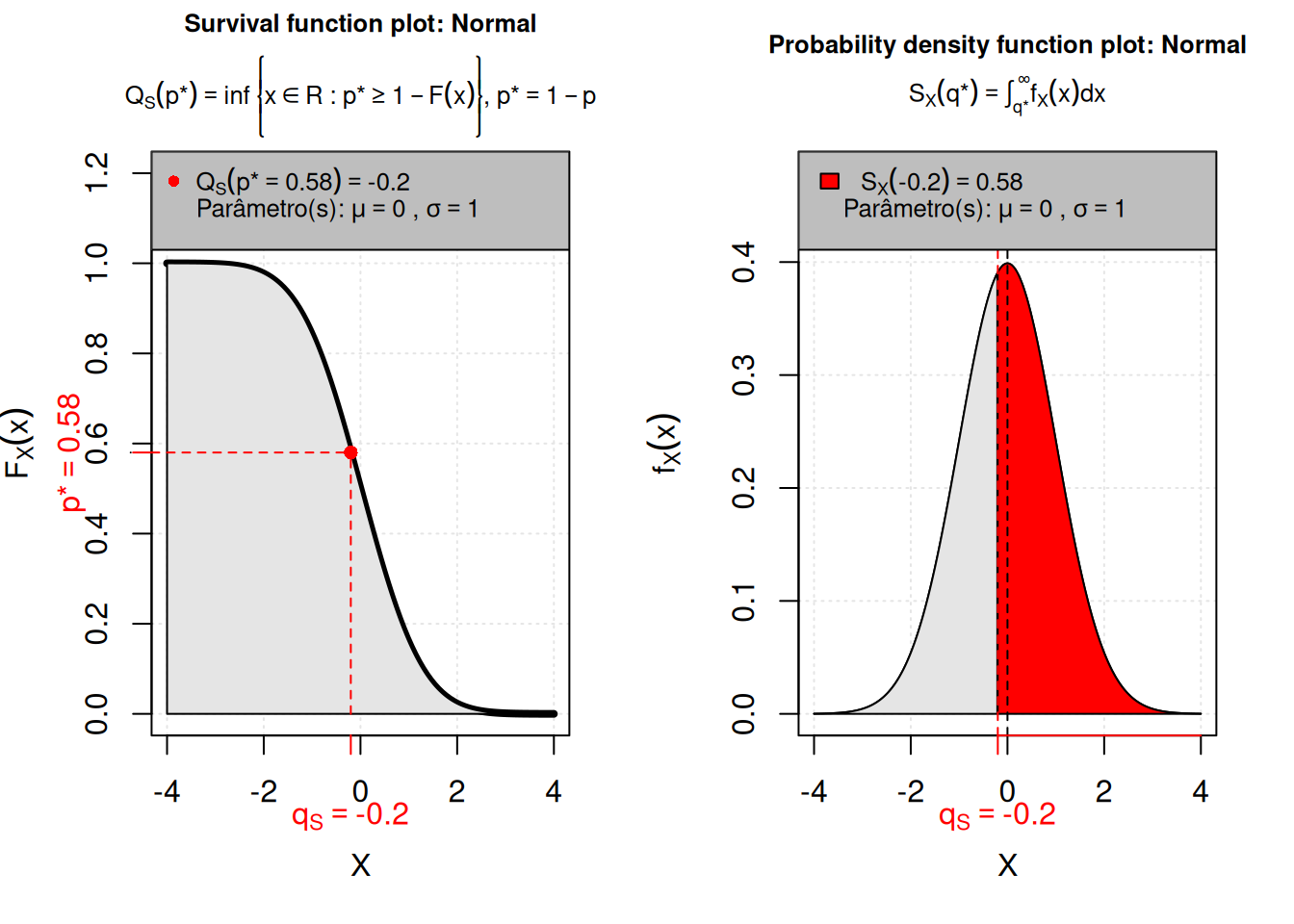

[1] -0.2

Isso implica que \(Z = -0,2\), logo, \(Z = - 0,20 \Rightarrow X = \mu + Z\sigma = 40 + (- 0,20) \times 6 = 38,8\).

  1. Para verificarmos o ponto que tem 5% de área acima dele, recorremos a função R Q(), isto é,
Q(0.05, mean = 0, sd = 1, lower.tail = F)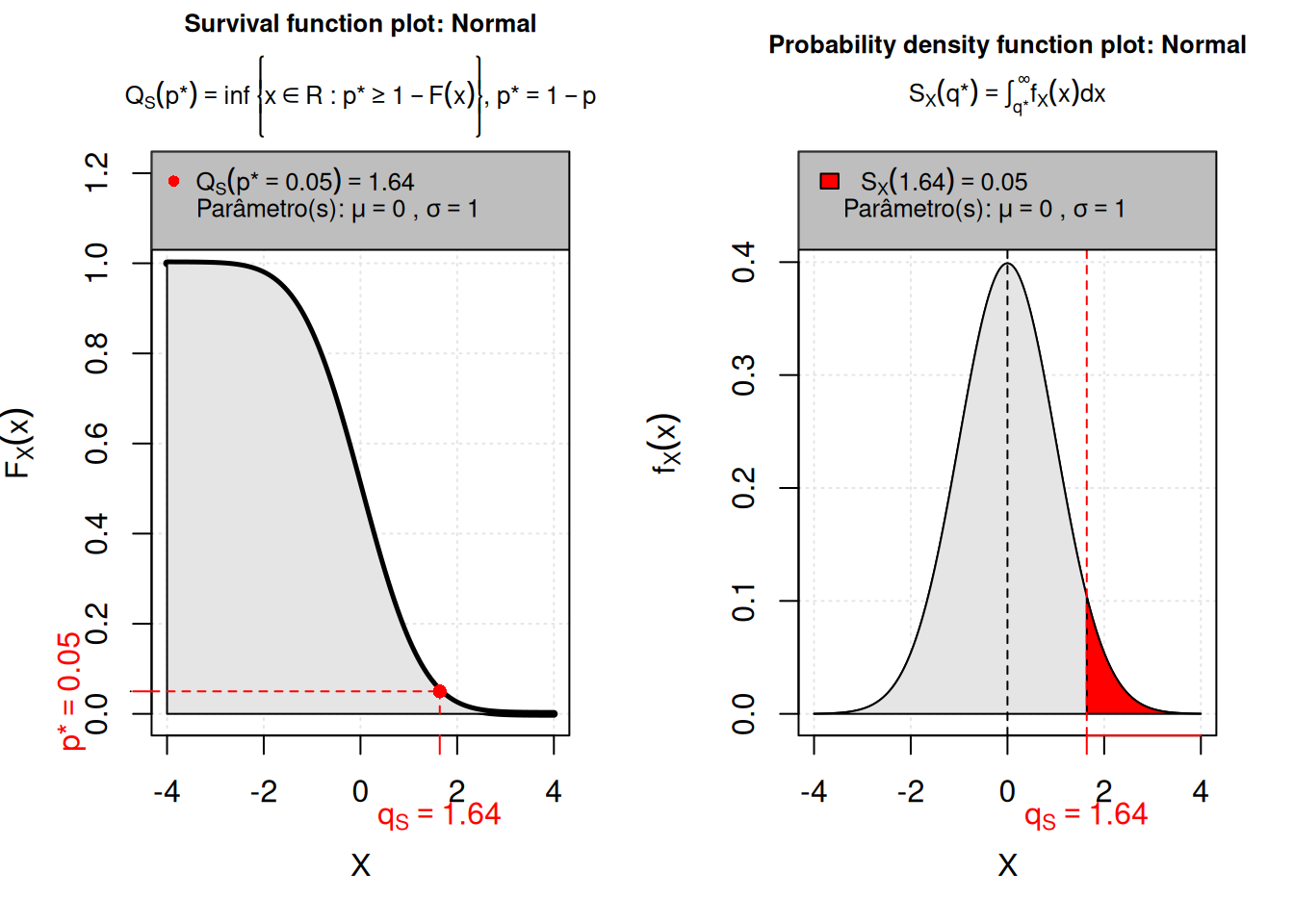

[1] 1.64

Isso implica que \(Z = 1,64\), logo, \(Z = 1,64 \Rightarrow X = \mu + Z\sigma = 40 + 1,64 \times 6 = 49,84\).

  1. \(P(Z > 0) = 0,5000\), isto é,
P(0, mean = 0, sd = 1, lower.tail = F)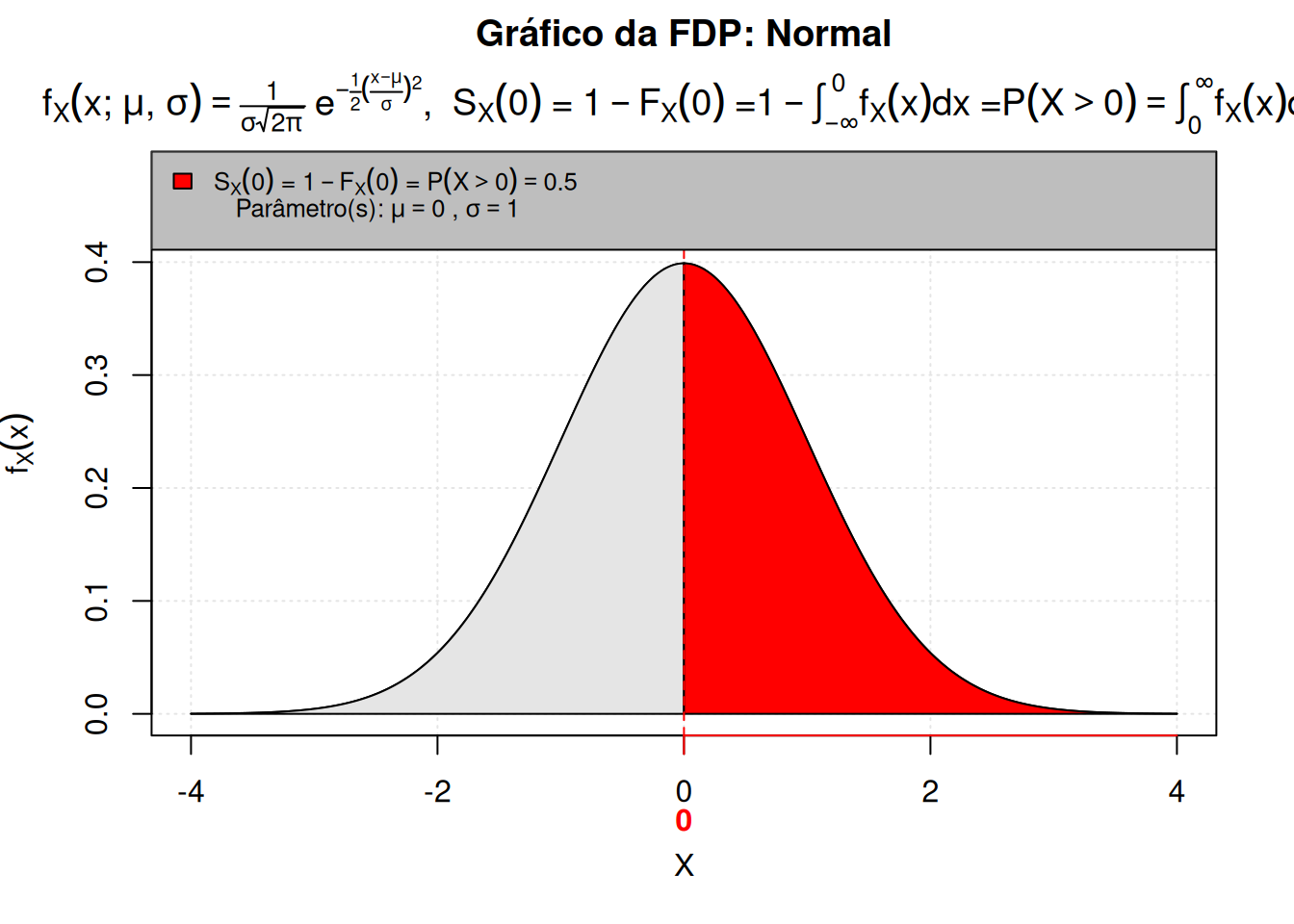

[1] 0.5

Exercício 6.5
Em um exame vestibular de matemática as notas distribuíram-se normalmente com média 6 o desvio padrão 1,5. Calcular o número de aprovados entre os 120 candidatos, sabendo-se que a nota mínima de aprovação é 5.

Exercício 6.6
Uma máquina de empacotar determinado produto apresenta variação de peso com desvio padrão de 20g. Em quanto deve ser regulado o peso médio do pacote para que apenas 10% tenham menos de 400g. Suponha distribuição normal dos pesos dos pacotes.

Exercício 6.7
Na 1ª prova de Estatística a média foi 4,5 e o desvio padrão 2,3. Considerando o método científico de aprovação:

  • Conceito A: nota média $ + $;
  • Conceito B: $ $ média $ + $;
  • Conceito C: $ - $ média $ $;
  • Conceito D: média \(\leq \mu - \sigma\);
  1. Quantos alunos receberam cada um dos conceitos?
  2. Quantos alunos foram aprovados (Conceito A, B e C);
  3. Quantos alunos foram aprovados com distinção (média \(\geq \mu + 2\sigma\));
  4. Considere o método comum de aprovação (\(X \geq 5,0\)), quantos foram reprovados.

OBSERVAÇÃO: 100 alunos fizeram essa prova.

Exercício 6.8
Ao investir num determinado negócio, um cidadão pode ter um lucro anual de US$ 60.000 com probabilidade 0,3 ou tomar um prejuízo de US$ 20.000 com probabilidade 0,7. Qual é a sua esperança matemática?

Exercício 6.9

Considere que existem defeitos aleatórios na superfície de um chip semicondutor, e o fabricante informa que 5% de sua produção apresenta defeito. Desse modo, em uma amostra de 35 chips, qual a probabilidade de encontrarmos:

  1. nenhum defeito;
  2. apenas um defeito;
  3. não mais que um defeito;
  4. acima de dois defeitos.

Exercício 6.10
Considere uma avaliação de câmeras de uma determinada marca de celular, e que 85% dessas câmeras passaram no teste de avaliação, de modo que os celulares foram avaliados de modos independente. Qual o tamanho da amostra necessário para que a probabilidade de no mínimo uma câmera não tenha passado no teste seja no mínimo de 90%?

Exercício 6.11

Considere que o número de alterações em uma página web de entretenimentos seja modelada por uma distribuição de Poisson, e que ocorre em média 0,30 alterações por dia.

  1. Qual a probabilidade de que não haja alterações em um dia?
  2. Qual a probabilidade de ocorra mais do que uma alteração em 8 horas?
  3. Qual a probabilidade de ocorrer no máximo duas alterações em 2 dias?
  4. Qual o valor esperado dessas alterações por dia? E a variabilidade dessas alterações em torno de 0,30 alterações por dia?
Exercício 6.12

A probabilidade de um consumidor responder ao questionário de grau de satisfação em um site de compras, após a finalização da compra é de 5%. Considerando que 100 consumidores apresentam comportamentos independentes quanto ao interesse pelas compras nesse site, determine:

  1. nenhum consumidor responder ao questionário;
  2. mais de cinco consumidores responderem ao questionário;
  3. exatamente 15 pessoas responderem o questionário.
  4. a esperança de \(X\);
  5. a variância e o desvio padrão de \(X\);
Exercício 6.13

Considere o sistema de segurança de acesso a conta de usuários de um determinado banco, por meio de uma senha de 6 dígitos, com 26 caracteres (a-z) ou números (0-9). Um hacker tentou invadir o sistema, e com informações previlegiadas percebeu algumas informações sobre as senhas de clientes:

  1. Alguns clientes da carteira do banco apresentavam senhas com cinco letras e um número;
  2. Alguns clientes da carteira do banco apresentavam senhas com quatro letras seguidas por dois números.

Com isso, indagamos:

  1. foi selecionado ao acaso 10 clientes, qual a probabilidade de 2 clientes apresentarem senhas do tipo (I)?
  2. foi selecionado ao acaso 15 clientes, qual a probabilidade de nenhum cliente apresentar senha do tipo (II)?