📚 Ensino normal 2024.1
Sumário
Apresentação
Curso de Estatística e Probabilidade oferecido no formato presencial pela UFSJ, campus Alto Paraopeba (CAP), Ouro Branco/MG.
4 horas por semana, por 18 semanas
Tópicos abordados
Definições gerais. Coleta, organização de dados. Medidas de posição. Medidas de dispersão. Probabilidades. Distribuições de probabilidade. Amostragem. Teoria da estimação. Teoria da decisão. Correlação e regressão linear simples.
Onde?
- O curso é ministrado na UFSJ, campus Alto Paraopeba (CAP), para todos os cursos de Engenharia do campus.
- Todas as nossas estão gravadas:
- canal: http://youtube.com/bendeivide
- Período:
- Aulas presenciais:
- Engenheria Química:
- segunda-feira (21:00 - 23:00, sala 207.4)
- terça-feira (21:00 - 23:00, sala 207.4)
- Engenharia Mecatrônica:
- quinta-feira (19:00 - 21:00, sala 202.4)
- sexta-feira (21:00 - 23:00, sala 202n .4)
- Engenheria Química:
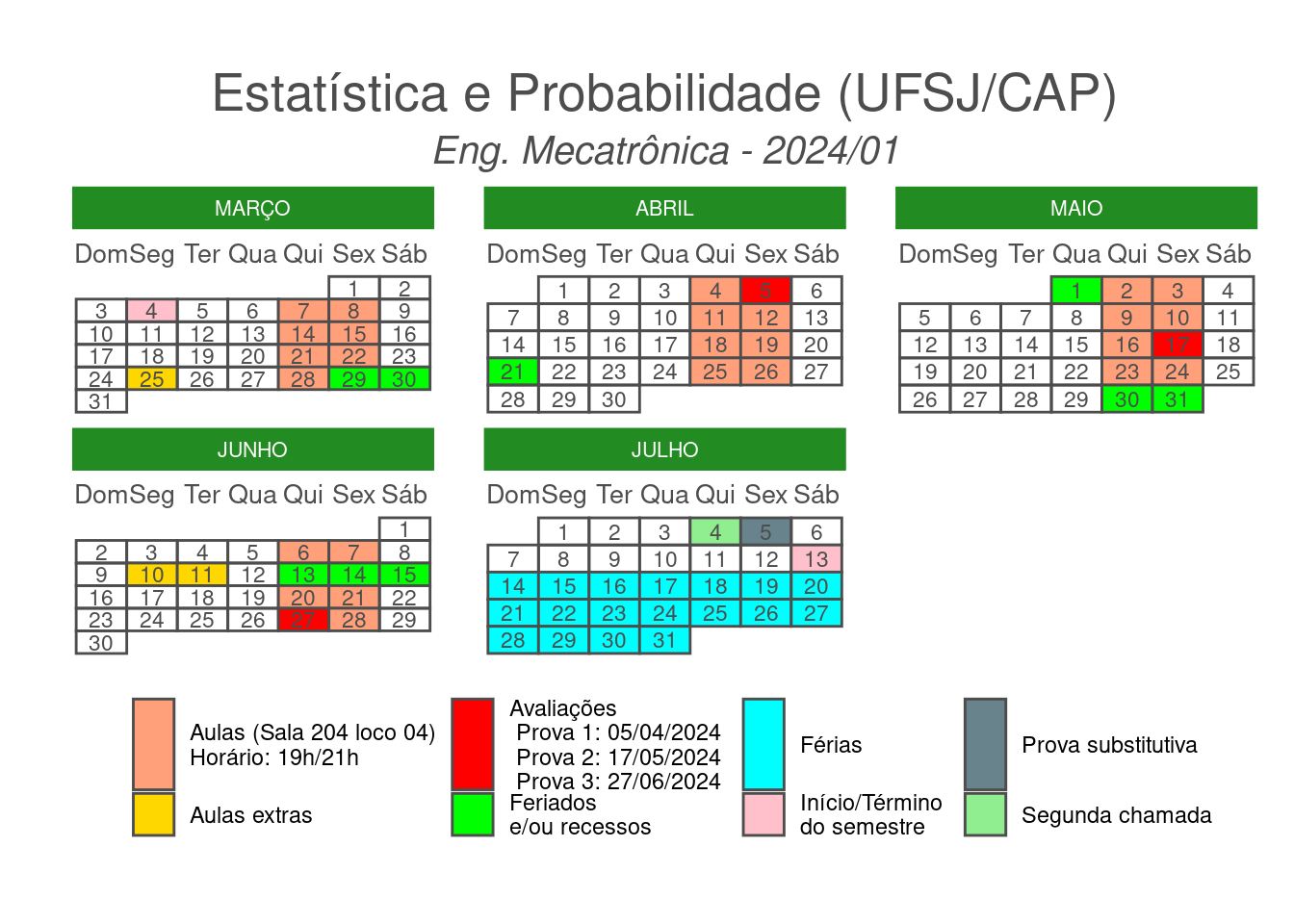
Calendário e Cronograma
- Calendário

Grupo de Whatsapp
Preenchimento de dados para as avaliações
Notas
Ementa
Nós usamos a ementa contida nos Projetos Pedagógicos de Cursos (PPCs) da CAP/UFSJ
Acesse a ementa do curso
- DEFINIÇÕES GERAIS E TÉCNICAS DE SOMATÓRIO:
- Introdução
- Definições Gerais
- Técnicas de somatório
- COLETA, ORGANIZAÇÃO E APRESENTAÇÃO DE DADOS:
- Introdução
- Representação tabular
- Representação gráfica
- MEDIDAS DE POSIÇÃO:
- Introdução
- Média
- Mediana
- Moda
- MEDIDAS DE DISPERSÃO:
- Introdução
- Amplitude total
- Variância
- Desvio Padrão
- Coeficiente de Variação
- Erro padrão da Média
- PROBABILIDADES:
- Conceitos básicos
- Definições de probabilidades
- Propriedades
- Eventos independentes e probabilidade condicional
- Teorema de Bayes
- Função de probabilidade discreta
- Função de probabilidade contínua
- Função de distribuição de probabilidade acumulada
- Esperança matemática e variância
- DISTRIBUIÇÕES DE PROBABILIDADES:
- Introdução
- Distribuições discretas de probabilidades
- Distribuições contínuas de probabilidades
- AMOSTRAGEM:
- Introdução
- Amostragem não-probabilística e probabilística
- Técnicas de amostragem probabilística
- DISTRIBUIÇÃO DE AMOSTRAGEM:
- Introdução
- Distribuição de amostragem da média
- Distribuição de amostragem de proporções
- Distribuição de amostragem de diferença entre médias
- Distribuições amostrais (qui-quadrado, t e F)
- TEORIA DA ESTIMAÇÃO:
- Introdução
- Conceitos básicos
- Tipos de estimativas
- Propriedades de um estimador
- Estimação por ponto
- Estimação por intervalo:
- Intervalo de confiança para a média
- Intervalo de confiança para a variância
- Intervalo de confiança para a diferença entre médias
- Dimensionamento de amostras
- TEORIA DA DECISÃO:
- Introdução
- Testes de hipóteses
- Erros tipo I e II
- Teste unilateral e bilateral
- Passos para a construção de um teste de hipóteses
- Teste de hipóteses para a média
- Teste de hipóteses para a proporção
- Teste de hipóteses para a variância
- Teste de hipóteses para a diferença entre médias
- CORRELAÇÃO E REGRESSÃO LINEAR SIMPLES:
- Introdução
- Correlação linear:
- Coeficiente de correlação linear
- Teste de hipóteses acerca do coeficiente de correlação linear
- Regressão linear simples:
- Modelo
- Estimação dos parâmetros do modelo
- Teste de hipóteses para o modelo de regressão
- Medidas de adequação do modelo
Metodologia
Nossas aulas serão divididas de acordo com as 18 semanas de aula. As aulas serão expositivas e dialogadas com os alunos presencialmente ou via portal didático, constituída pela seguinte estratégia de ensino:
- Motivação:
- Levantamento do conhecimento prévio dos alunos em relação ao tema;
- Apresentação de algumas situações práticas para a compreensão dos tópicos a serem abordados;
- Exposição dos objetivos da aula.
- Desenvolvimento:
- Introdução ao assunto abordado;
- Apresentação de definições e teoremas envolvidos;
- Aplicação de softwares estatísticos, quando for pertinente;
- Exemplos e aplicações na estatística e área do curso, do assunto abordado.
Detalhamento da metodologia
As aulas seguirão um modelo de metodologia ativa baseado nas coreografias didáticas. Criaremos um cenário em que o propagador de conhecimento também seja produzido pelo aluno. Ele será o protagonista. Desta forma, traremos métodos de aprendizagem do tipo “ensinar por aprender”.
Nossas aulas estarão disponíveis em http://bendeivide.github.io/. Para os alunos matriculados na disciplina, também será possível acompanhar o material pelo portal didático. Nossas aulas terão 4 (quatro) horas semanais de aulas presenciais, um total de 72h**.
Iremos utilizar diversas ferramentas do google como os seus editores de textos, planilhas e apresentadores. Também utilizaremos o overlief para usuários de LaTeX. Com a linguagem R, mostraremos documentos dinâmicos, usando o R Markdown e o shiny, também para o desenvolvimento de materiais didáticos, quanto para as atividades com os alunos. Todas essas ferramentas tecnológicas são gratuitas e de fácil instalação para os alunos, uma vez que dareremos todo o suporte, de forma que os alunos estejam capacitados a utilizar todas as ferramentas quando necessário.
Avaliação
Segue um detalhamento das nossas avaliações
Serão distribuídos 100 pontos para atividades avaliativas da seguinte forma:
- 1ª Avaliação - Seções 1, 2, 3, e 4 - 20 pontos;
- 2ª Avaliação - Seções 5, 6, 7 e 8 - 30 pontos;
- 3ª Avaliação - Seções 9, 10 e 11 - 30 pontos;
- Trabalhos (Trabalhos, Exercícios, Testes Rápidos e laudas de artigos) - 20 pontos;
Uma outra alternativa é desenvolvermos ideias de modo que o alunos possa contribuir com a disciplina, tais como criação de materiais didáticos, vídeo-aulas, etc. O objetivo é torná-lo parte integrante do conhecimento formado dentro de sala de aula. Dessa forma, com essa adesão, o aluno pode está isento das avaliações, e ser avaliado de acordo com as entregas semanais do que for acordado entre aluno e professor. Este ponto aglutina diversos projetos, principalmente o Aprender por ensinar, LEEM, statscience, Rapidinhas do R, dentre outros que possam surgir no processo. Por fim, o aluno acordará um contrato de quais demandas devem ser entregues e quais os direitos e deveres a ele imposto, para que isso possa ser possível mensurar a sua aprendizagem na disciplina.
Para ser aprovado o aluno deverá obter nota final maior ou igual a 60 pontos e não poderá faltar mais de 25% das aulas. O discente que não for aprovado por nota poderá fazer uma prova substitutiva, incluindo todo o conteúdo da disciplina, que substituirá a menor nota dentre as três avaliações.
O discente que perder alguma avaliação teórica poderá fazer uma segunda chamada, desde que justificada via coordenadoria.
A perda de alguma avaliação deverá ser apresentado justificativa. Observações:
- São considerados motivos justiçados para fins de segunda chamada da avaliação teórica: exercício da função de representante discente nos órgãos colegiados ou diretor de entidades estudantis, desde que comprovado o comparecimento a reunião e ou encontros pertinentes a representação no dia e horário da referida avaliação (art. 142 e 143 do Regimento Geral da UFSJ); doença infecto-contagiosa ou internação, desde que esta esteja comprovada por meio atestado médico, contendo CID;
- Motivos pessoais, profissionais e atestados de consultas médicas eletivas não são considerados como motivos justificados para que o discente tenha direito a segunda chamada de avaliação teórica;
- Na educação superior não há abono de faltas, exceto nos seguintes casos: discente reservistas - Lei 4375, 17 de agosto de 1964; discente designado para compor a Comissão Nacional de Avaliação da Educação Superior (CONAES) que, em decorrência da designação, tenha participado de reuniões da CONAES em horário coincidente com as atividades acadêmicas (\S 5º do Art. 7º da Lei 10.861/2004). Portanto, atestados médicos, de trabalho e de outras atividades acadêmicas, não dão direito a abono de falta, tais ausências são enquadradas no limites dos 25%, É para tais imprevistos que o aluno pode se ausentar em 25% das aulas;
- Nos casos de portadores de afecções (Decreto-lei 1044, de 21 de outubro de 1969) e estado de gestação (Lei 6202, de 17 de abril de 1975), o discente poderá solicitar Regime Especial como compensação de ausência às aulas. Em ambos os casos, a solicitação, acompanhada do respectivo atestado médico, deverá ser protocolada na DICON, no início do impedimento.
Bibliografia adotada para a disciplina
Bibliografia detalhada
- MONTGOMERY, Douglas C.; RUNGER, George C.. Estatística aplicada e probabilidade para engenheiros. 6. ed. Rio de Janeiro: LTC, 2016. 629 p. Tradução de: Verônica Calado.
- DEVORE, J. L.. Probabilidade e Estatística: para engenharia e ciências. São Paulo: Pioneira Thomson, 2006. 692 p.
- MORETTIN, Luiz Gonzaga. Estatística Básica: Probabilidade e Inferência. São Paulo: Pearson Prentice Hall, 2010. 375 p.
- BUSSAB, W. O.; MORETTIN, P.A. Estatística Básica. 5. ed. São Paulo: Saraiva, 2003.
- COSTA NETO, P. L. O. Estatística. 3. ed. São Paulo: Edgard Blucher, 2007.
- TRIOLA, M. F. Introdução à Estatística. Rio de janeiro: LTC, 2008.
Material adotado
- Livro referência: EPAEC
- Sugestões e críticas sobre o livro podem ser enviadas para livrosdeben@gmail.com
Materiais complementares
- Estatística Básica (Departamento de Estatística, UFPR)
- Estatística Aplicada (Tales Jesus Fernandes, UFLA)
- Resumo do Livro Estatística Básica (Daniel Furtado, UFLA)
- Estatística e Probabilidade (UECE)
- Estimação Estatística (Assis, et. al. 2021)
- Introdução à estatística com R (Eric Ferreira & Marcelo Oliveira )
- Introdução a linguagem R: seus fundamentos e práticas (Pedro Faria & João Parga)
- Teste de Hipóteses Estatísticas (Janilson Pinheiro de Assis et. al., UFERSA)
- Glossário de Estatística (Janilson Pinheiro de Assis, UFERSA)
- Canal Ciência Estatística
- Estatística e Probabilidade: Exercícios (Assis et. al., 2023)
Metodologias ativas
Aprender por ensinar
- Modelo de Arquivo em power point
- Resultado em vídeo
- Os programas necessários:
- Editor de Slides: o MS Power Point (Instalado previamente no Windows); LibreOffice;
- Gravador de tela e de seu áudio: OBS Studio OBS.: Os programas são esses. Qualquer dúvida, favor me procurar.
Mapas Mentais
- Dúvidas de como desenvolver, faça uso dos buscadores na internet, vídeo-aulas, etc. Há muito material interessante na internet;
- Modelo
Resumo de Cornell
- Dúvidas de como desenvolver, faça uso dos buscadores na internet, vídeo-aulas, etc. Há muito material interessante na internet;
- Modelo
Como estudar e aprender
Vídeoaula do Prof. Pierluigi Piazzi (Youtube: Canal Glauco Copeck XYZ)
Aulas
🎓 Aula 1
Temas: Apresentação do curso e Definições gerais da estatística e técnicas de somatório (Capítulo 1)
Apresentação: Aula 01
Tempo: 1h 50min.
Podcast
Material para consulta
Vídeo-aulas
🎓 Aula 2
Temas: Exercícios sobre Definições gerais da estatística e técnicas de somatório (Capítulo 1)
Apresentação: Aula 02
Tempo: 1h 50min.
Podcast
Material para consulta
Vídeo-aulas
🎓 Aula 3
Temas: Coleta, organização e apresentação de dados
Apresentação: Aula 03
Tempo: 1h 50min.
Podcast
Material para consulta
Vídeo-aulas
🎓 Aula 4
Temas: Exercícios sobre Coleta, organização e apresentação de dados
Apresentação: Aula 04
Tempo: 1h 50min.
Podcast
Material para consulta
Vídeo-aulas
🎓 Aula 5
Tema: Medidas de posição
Apresentação: Aula 05
Tempo: 1h 50min.
Podcast
Material para consulta
Vídeo-aulas
🎓 Aula 6
Tema: Exercícios sobre Medidas de posição
Apresentação: Aula 06
Tempo: 1h 50min.
Podcast
Material para consulta
Vídeo-aulas
🎓 Aula 7
Tema: Medidas de dispersão
Apresentação: Aula 07
Tempo: 1h 50min.
Podcast
Material para consulta
Vídeo-aulas
🎓 Aula 8
Tema: Exercícios sobre Medidas de dispersão
Apresentação: Aula 08
Tempo: 1h 50min.
Podcast
Material para consulta
Vídeo-aulas
🎓 Aula 9
Tema: Revisão para a Prova 1
Apresentação: Aula 09
Tempo: 1h 50min.
Podcast
Material para consulta
Vídeo-aulas
🎓 Aula 10
Prova 1: Realizado em horário de aula. Acesse o cronograma de aulas para mais detalhes.
🎓 Aula 11
Tema: Probabilidades (Parte I e Parte II)
Apresentação: Aula 11 (Parte I) e Aula 11 (Parte II)
Tempo: 1h 50min.
Podcast
Plano de aula: Parte (I) e Parte (II)
Material para consulta
Vídeo-aulas
🎓 Aula 12
Tema: Probabilidades (Parte III)
Apresentação: Aula 12
Tempo: 1h 50min.
Podcast
Material para consulta
Vídeo-aulas
🎓 Aula 13
Tema: Exercícios sobre Probabilidades
Apresentação: Aula 13
Tempo: 1h 50min.
Podcast
Material para consulta
Vídeo-aulas
🎓 Aula 14
Tema: Distribuições de probabilidade (Parte I)
Apresentação: Aula 14
Tempo: 1h 50min.
Podcast
Material para consulta
Vídeo-aulas
🎓 Aula 15
Tema: Distribuições de probabilidade (Parte II)
Apresentação: Aula 15
Tempo: 1h 50min.
Podcast
Material para consulta
Vídeo-aulas
🎓 Aula 16
Tema: Exercícios sobre Distribuições de probabilidade
Apresentação: Aula 16
Tempo: 1h 50min.
Podcast
Material para consulta
Vídeo-aulas
🎓 Aula 17
Em aula!
🎓 Aula 18
Em aula!
🎓 Aula 19
Em aula!
🎓 Aula 20
Em aula!
🎓 Aula 21
Em aula!
🎓 Aula 22
Prova 02
🎓 Aula 23
Em aula!
🎓 Aula 24
Em aula!
🎓 Aula 25
Em aula!
🎓 Aula 26
Em aula!
🎓 Aula 27
Em aula!
🎓 Aula 28
Em aula!
🎓 Aula 29
Em aula!
🎓 Aula 30
Em aula!
🎓 Aula 31
Em aula!
🎓 Aula 32
Em aula!
🎓 Aula 33
Prova 3
🎓 Aula 34
Palestra
🎓 Aula 35
Segunda chamada
🎓 Aula 36
Prova substitutiva
Veja também
- Ensino remoto 2021.2
- Ensino remoto 2022.1
- Podcasts
- Exercícios resolvidos
- Curso EAR: R básico
- Cantando com a Estatística
- Vídeos
- Resumos da Estatística
Quiz
Quais as datas de avaliação?
Acessem: Avaliação e Cronograma
Como acessar o material de apoio?
- Acessem: Livro EPAEC
- Sugestões e críticas sobre o livro podem ser enviadas para livrosdeben@gmail.com.