2  Coleta, Organização e Apresentação de Dados

2.1 Introdução

O material básico com que o pesquisador trabalha são os dados provenientes de variáveis, sendo que a coleta destes é o passo inicial na avaliação estatística de uma pesquisa. Os dados da forma como foram coletados representam os dados brutos, e sempre se apresentam desordenados. Os dados colocados em ordem crescente ou decrescente representam os dados elaborados.

O passo seguinte é sintetizar os valores que uma ou mais variáveis podem assumir, para que se tenha uma visão global da variação dessa ou dessas variáveis. Inicialmente esses valores são apresentados em tabelas e gráficos, que irão nos fornecer rápidas e seguras informações a respeito das variáveis em estudo.

2.2 Representação Tabular

Uma tabela é um quadro que resume um conjunto de dados. Segundo Crespo (2009), uma tabela pode ser dividida em duas partes: principais e secundárias. As partes principais são:

1. Corpo: Conjunto de linhas e colunas que contêm informações sobre a variável em estudo.
2. Cabeçalho: Parte superior da tabela que especifica o conteúdo das colunas.
3. Coluna indicadora: Parte da tabela que especifica o conteúdo das linhas.
4. Linhas: Retas imaginárias que facilitam a leitura no sentido horizontal, de dados que se inscrevem nos seus cruzamentos com as colunas.
5. Casa ou célula: Espaço destinado a um só valor.

As partes secundárias são:

1. Título: Conjunto de informações as mais completas possíveis. Deve responder as seguintes perguntas: O quê? Quando? Onde?, relativas à variável estudada.
2. Rodapé: É um espaço na parte inferior da tabela utilizado para colocar informações necessárias referentes aos dados.
3. Fonte: É a indicação da entidade responsável pela elaboração da tabela. Deve ser colocada no rodapé, no final da tabela. Esse procedimento garante a honestidade científica e serve como indicativo para posteriores consultas.
4. Notas: Também podem ser colocadas no rodapé, depois da fonte, de forma sintética. As notas têm caráter geral, referindo-se à totalidade da tabela. Devem ser enumeradas em algarismos romanos, quando existirem duas ou mais.
5. Chamadas: As chamadas têm caráter particular, referindo-se a um item específico da tabela. São enumeradas em algarismos arábicos, entre parênteses.

A seguir será abordado o Exemplo 2.1 para se observar o desenvolvimento de uma tabela.

Exemplo 2.1 Considere o exemplo de tabela a seguir, que representa a produção de grãos, em ordem decrescente da quantidade produzida, segundo os principais produtos agrícolas, Brasil, 2005.

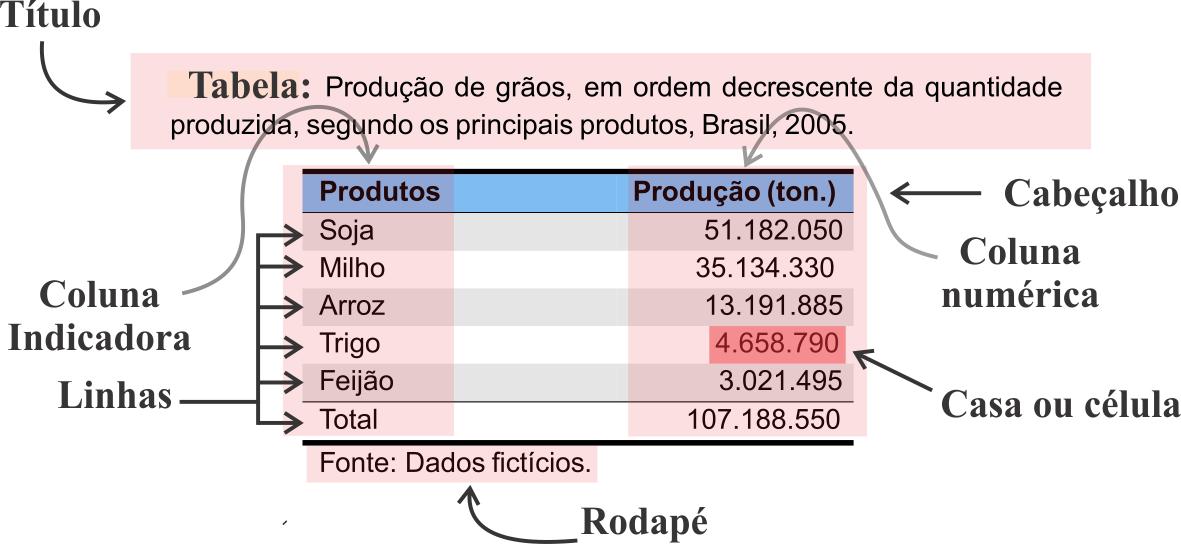
2.2.1 Tabela de distribuição de frequências

Um das maneiras de se organizar e resumir um conjunto de dados é através de uma tabela de distribuição de frequências, sendo que estas permitem identificar características de interesse dos dados sob análise. Essas tabelas podem ser de dois tipos:

1. tabela de distribuição de frequências simples¹: Os dados são agrupados sem intervalos de classes com as respectivas frequências de ocorrência.
2. Tabela de Distribuição de Frequências com dados agrupados em intervalos de classes: Os dados são agrupados em intervalos de classes com as respectivas frequências de ocorrência.

Na Tabela de Distribuição de Frequências, podem ser identificadas as seguintes frequências:

1. Absoluta \((F_i)\)}: Número de dados ocorridos em cada nível ou categoria da variável sob estudo. A soma das frequências absolutas corresponde ao total de dados (tamanho da amostra ou população);
2. Relativa \((Fr_i)\)}: Obtida pela divisão da frequência absoluta pelo número total de dados;
3. Percentual \((Fp_i)\)}: Frequência relativa multiplicada por 100;
4. Frequência acumulada para baixo \((Fc\downarrow)\)}: Mostra quantos dados são menores que um determinado valor;
5. Frequência acumulada para cima \((Fc\uparrow)\)}: Mostra quantos dados são maiores que um determinado valor.

Para se organizar um conjunto de dados em uma tabela de distribuição de frequências, primeiro deve-se conhecer qual é o tipo de informação que se está trabalhando, isto é, que tipo de variável correspondem os dados coletados, se qualitativos ou quantitativos.

2.2.1.1 Variáveis qualitativas

No caso de variáveis qualitativas, nominal ou ordinal, utiliza-se de uma tabela de distribuição de frequências simples para se organizar e resumir tais variáveis, sendo apresentado o Exemplo 2.2 a seguir.

Exemplo 2.2 Um Engenheiro Agrônomo conduziu um estudo com o objetivo de se conhecer o nível de tecnificação (baixo, médio ou alto), adotado pelos produtores rurais da região do Alto Rio Grande, sul de Minas Gerais. Foi avaliada uma amostra de 50 produtores rurais e os resultados estão apresentados na Tabela 2.1.

Tabela 2.1: Nível de tecnificação adotado pelos produtores rurais da região do Alto Rio Grande, sul de Minas Gerais, 2007 (dados brutos).

Baixo	Baixo	Alto	Médio	Médio
Baixo	Alto	Médio	Alto	Médio
Alto	Baixo	Alto	Médio	Médio
Baixo	Médio	Baixo	Médio	Médio
Médio	Médio	Médio	Médio	Baixo
Médio	Baixo	Médio	Médio	Médio
Alto	Baixo	Alto	Médio	Médio
Baixo	Médio	Médio	Baixo	Alto
Baixo	Alto	Médio	Médio	Médio
Médio	Médio	Baixo	Médio	Médio

O próximo passo é ordenar os dados pelo nível de tecnificação (baixo, médio e alto), obtendo-se os dados elaborados dispostos na Tabela 2.2.

Tabela 2.2: Nível de tecnificação adotado pelos produtores rurais da região do Alto Rio Grande, sul de Minas Gerais, 2007 (dados elaborados).

Baixo	Baixo	Médio	Médio	Médio
Baixo	Baixo	Médio	Médio	Alto
Baixo	Baixo	Médio	Médio	Alto
Baixo	Médio	Médio	Médio	Alto
Baixo	Médio	Médio	Médio	Alto
Baixo	Médio	Médio	Médio	Alto
Baixo	Médio	Médio	Médio	Alto
Baixo	Médio	Médio	Médio	Alto
Baixo	Médio	Médio	Médio	Alto
Baixo	Médio	Médio	Médio	Alto

A seguir conta-se o número de produtores rurais com nível de tecnificação baixo, médio e alto, ou seja, a frequência absoluta, e organiza-se os dados em uma tabela, dividida em classes (baixo, médio e alto) com as respectivas frequências de ocorrência. Os resultados estão apresentados na Tabela 2.3.

Tabela 2.3: Nível de tecnificação adotado pelos produtores rurais da região do Alto Rio Grande, sul de Minas Gerais, 2007.²

Nível de Tecnificação	\(\mathbf{F_i}\)	\(\mathbf{Fr_i}\)	\(\mathbf{Fp_i(\%)}\)
Baixo	13	0,26	26,0
Médio	28	0,56	56,0
Alto	9	0,18	18,0
Total	50	1,00	100,0

Observando os resultados da Tabela 2.3, tem-se que 56,0% dos produtores rurais adotam em suas propriedades um nível médio de tecnologia, porém apenas 18,0% empregam altas tecnologias, e 26,0% utilizam-se de baixas tecnologias de produção. Esses resultados pode orientar melhor os trabalhos dos Extensionistas que trabalham na região.

2.2.1.2 Variáveis quantitativas

1. Discretas: Se os dados de uma amostra ou população estiverem representados por variáveis quantitativas discretas, eles estarão naturalmente classificados, isto é, separados em grupos distintas. Para se ter uma ideia do modo como os dados se distribuem, basta escrever em uma coluna os valores da variável discreta estudada em ordem crescente e, assinalar em outra coluna paralela, o número de vezes em que cada um desses valores foi observado, isto é, a frequência absoluta de cada valor. Neste caso utiliza-se de uma tabela de distribuição de frequências simples para se organizar e resumir tais variáveis, sendo apresentado no Exemplo 2.3.

Exemplo 2.3 Um Engenheiro Agrônomo examinou um lote de 150 caixas de banana maçã, escolhidos aleatoriamente num carregamento de 10.000 caixas, no CEAGESP de São Paulo, SP, anotando o número de pencas com empedramento. Os dados estão apresentados na Tabela 2.4.

Tabela 2.4: Número de pencas de banana maçã com empedramento (dados brutos).

2	3	1	1	0	0	2	2	3	5
4	0	4	0	1	1	0	6	5	0
1	1	0	4	0	0	5	0	0	2
0	4	5	0	4	0	2	1	1	1
2	0	0	1	0	4	0	5	0	0
0	5	0	4	1	0	1	0	2	1
0	1	1	0	2	5	0	2	0	0
3	5	0	1	0	0	1	4	3	3
2	0	4	0	3	4	0	0	1	1
0	2	1	3	2	1	2	3	1	0
1	5	2	2	1	2	1	1	2	3
3	2	6	1	5	3	2	1	1	1
6	2	2	4	1	4	1	6	3	4
1	4	1	3	3	1	3	2	4	1
3	1	3	2	2	3	2	3	4	3

Após coletar os dados o Engenheiro Agrônomo ordenou os dados em ordem crescente, obtendo-se assim os dados elaborados apresentados na Tabela 2.5.

Tabela 2.5: Número de pencas de banana maçã com empedramento (dados elaborados).

0	0	0	1	1	2	2	3	4	4
0	0	0	1	1	2	2	3	4	5
0	0	0	1	1	2	2	3	4	5
0	0	0	1	1	2	2	3	4	5
0	0	0	1	1	2	2	3	4	5
0	0	0	1	1	2	2	3	4	5
0	0	0	1	1	2	2	3	4	5
0	0	0	1	1	2	2	3	4	5
0	0	1	1	1	2	2	3	4	5
0	0	1	1	1	2	2	3	4	5
0	0	1	1	1	2	3	3	4	5
0	0	1	1	1	2	3	3	4	6
0	0	1	1	1	2	3	3	4	6
0	0	1	1	1	2	3	3	4	6
0	0	1	1	1	2	3	3	4	6

Ordenado os dados o Engenheiro Agrônomo examinou as 150 caixas, e contou quantas caixas tinham nenhuma penca empedrada, quantas tinham uma penca empedrada, duas pencas empedradas e assim por diante, e organizou os dados com as respectivas frequências de ocorrência na Tabela 2.6.

Tabela 2.6: Número de pencas de banana maçã com empedramento, CEAGESP, São Paulo, SP, 2007.³

Número de pencas empedradas	\(\mathbf{F_i}\)	\(\mathbf{Fr_i}\)	\(\mathbf{Fp_i(\%)}\)
0	38	0,2533	25,33
1	37	0,2467	24,67
2	25	0,1667	16,67
3	20	0,1333	13,33
4	16	0,1067	10,67
5	10	0,0667	6,67
6	4	0,0266	2,66
Total	150	1,0000	100,00

Observa-se pelos resultados apresentados na Tabela 2.6 que: das \(150\) caixas de banana inspecionadas, apenas \(38\) caixas, ou seja, \(25,33\%\), não tinham nenhuma penca empedrada, e que \(10,67\%\) tinham \(4\) pencas empedradas. Estes resultados poderiam estar orientando o Engenheiro Agrônomo a direcionar suas ações, no sentido de melhorar a qualidade do produto.

2. Contínuas: Quando os dados de uma amostra ou população estiverem representados por variáveis quantitativas contínuas, é evidente que não existem classes naturais. Apesar disso pode-se usar o recurso de agrupar os dados em classes com um determinado número de intervalos. Tais classes terão dois valores limites, isto é, um limite inferior e um limite superior. Assim, utiliza-se de uma tabela de distribuição de frequências com dados agrupados em classes com intervalos de classes, para se organizar e resumir tais variáveis.

Neste casso para a construção da tabela de distribuição de frequências devem ser seguidos os seguintes passos:

1. Determinar o número de classes \((K)\): A escolha do número de classes é arbitrária, e a experiência do pesquisador com os dados é que lhe indicará quantas classes devem ser usadas. No entanto deve ser observado que, com poucas classes perde-se informação, e com muitas classes o objetivo de se resumir um conjunto de dados pode ficar prejudicado. Pode-se, também, adotar o critério baseado no número de observações “\(n\)”, conforme Tabela 2.7.

Tabela 2.7: Determinação do número de classes (\(K\)).

Número de observações \((n)\)	Número de classes \((K)\)
Até \(100\)	\(\sqrt{n}\) (inteiro mais próximo)
Acima de \(100\)	\(5\log_{10}(n)\) (inteiro mais próximo)

2. Determinar a amplitude de classe \((c)\): A amplitude de classe é definida pela diferença entre os limites superior e inferior de uma determinada classe, dada por: \[ c=LS_{i} - LI_{i}, \] para \(i\) \(=\) \(1\), \(2\), \(\ldots\), \(K\), sendo \(K\) o número de classes. Porém, em termos práticos a amplitude de classe é determinada da seguinte forma: \[ c=\frac{A}{K-1}, \] em que:

   • \(A\) é amplitude total, que representa a diferença entre a maior observação e a menor observação;
   • \(K\) é o número de classes.

3. Determinar o limite inferior da primeira classe \((LI_{1ª})\), dado por:

\[ LI_{1ª} = \textrm{Menor dado} - \frac{c}{2}. \]

4. Determinar o limite superior da primeira classe (\(LS_{1ª}\)), dado por:

\[ LS_{1ª} = LI_{1ª} + c. \]

5. Os demais limites de classe são obtidos somando-se o valor de \(c\) até completar as \(K\) classes.
6. Determinar os pontos médios das classes \((\tilde{X}_i)\), dado por:

\[ \tilde{X}_i=\frac{LI_{iª}+LS_{iª}}{2}. \]

Posteriormente, serão determinados as frequências: absoluta \((F_i)\), relativa \((Fr_i)\) e percentual \((Fp_i)\), de forma similar como foi desenvolvido na tabela de distribuição de frequência simples. Em geral usa-se as seguintes notações para os intervalos de classes: \([a;b)\) ou \(a \vdash b\).

Na contagem do número de dados contidos em um intervalo de uma determinada classe (frequência absoluta), deve-se incluir o valor do limite inferior \((a)\) e excluir o valor do limite superior \((b)\) de cada classe. O valor do limite superior passa a ser contado na classe posterior.

Exemplo 2.4 Um Zootecnista observou os pesos ao nascer, em kg, de uma amostra de 50 bezerros da raça nelore, provenientes da Fazenda de um grande criador. Os resultados estão apresentados na Tabela 2.8.

Tabela 2.8: Pesos ao nascer, em kg, de 50 bezerros da raça nelore (dados brutos).

26,8	24,3	23,7	31,0	22,2	25,2	29,5	24,2	33,0	27,2
25,9	23,0	25,6	26,5	26,0	22,8	31,8	21,0	29,3	27,8
24,1	26,9	24,5	26,2	29,8	21,6	27,2	26,8	26,9	25,0
29,6	31,3	22,1	26,1	29,2	25,3	26,0	27,2	28,1	26,2
28,5	27,2	28,6	25,8	26,5	28,1	24,9	30,5	28,7	24,5

Os dados foram colocados em ordem crescente e estão apresentados na Tabela 2.9.

Tabela 2.9: Pesos ao nascer, em kg, de 50 bezerros da raça nelore (dados elaborados).

21,0	23,0	24,5	25,3	26,0	26,5	27,2	28,1	29,2	30,5
21,6	23,7	24,5	25,6	26,1	26,8	27,2	28,1	29,3	31,0
22,1	24,1	24,9	25,8	26,2	26,8	27,2	28,5	29,5	31,3
22,2	24,2	25,0	25,9	26,2	26,9	27,2	28,6	29,6	31,8
22,8	24,3	25,2	26,0	26,5	26,9	27,8	28,7	29,8	33,0

Para a construção da Tabela de Distribuição de Frequências devem ser seguidos os passos descritos anteriormente, obtendo-se os seguintes resultados:

1. Número de classes \((K)\): \[ K=\sqrt{n}=\sqrt{50}=7,0711 \Rightarrow K=7~\textrm{classes}. \]

2. Amplitude de classe \((c)\): \[\begin{align*} c &= \frac{A}{K-1}\\ &=\frac{\textrm{Maior dado} - \textrm{Menor dado}}{K-1}\\ &= \frac{33,0-21,0}{7-1}\\ &=\frac{12}{6}\\ &=2,0~\textrm{kg}. \end{align*}\]

3. Limite inferior da primeira classe (\(LI_{1ª}\)): \[\begin{align*} LI_{1ª} &= \textrm{Menor dado}-\frac{c}{2}\\ &= 21,0-\frac{2,0}{2}\\ &=20,0~\textrm{kg}. \end{align*}\]

4. Limite superior da primeira classe (\(LS_{1ª}\)): \[\begin{align*} LS_{1ª} &= LI_{1ª}+c\\ &= 20,0+2,0 = 22,0~\textrm{kg}. \end{align*}\]

5. Demais limites:

Os demais limites dos intervalos de classe são obtidos somando-se o valor de \(c\) até completar as \(K\) classes.

1ª classe: \(20,0\) a \(22,0\) kg;
2ª classe: \(22,0\) a \(24,0\) kg;
3ª classe: \(24,0\) a \(26,0\) kg;
4ª classe: \(26,0\) a \(28,0\) kg;
5ª classe: \(28,0\) a \(30,0\) kg;
6ª classe: \(30,0\) a \(32,0\) kg;
7ª classe: \(32,0\) a \(34,0\) kg.

6. Tabela de distribuição de frequências:

Obtidos os intervalos de classes são contados o número de dados que estão contidos em cada intervalo, ou seja, a frequência absoluta \((F_i)\). São determinados também as frequências relativa \((Fr_i)\) e percentual \((Fp_i)\) de cada classe, e o ponto médio de classe \((\tilde{X}_i)\).

E assim, constrói-se a tabela de distribuição de frequências, conforme a Tabela Tabela 2.10.

Tabela 2.10: Pesos ao nascer, em kg, de 50 bezerros da raça nelore, Fazenda XX, 2007.⁴

Peso \(\mathbf{(kg)}\)	\(\mathbf{\tilde{X}_i}\)	\(\mathbf{F_i}\)	\(\mathbf{Fr_i}\)	\(\mathbf{Fp_i(\%)}\)
\(\left[20,0 \right. ; \left. 22,0\right)\)	21,0	2	0,04	4,0
\(\left[22,0 \right. ; \left. 24,0\right)\)	23,0	5	0,10	10,0
\(\left[24,0 \right. ; \left. 26,0\right)\)	25,0	12	0,24	24,0
\(\left[ 26,0 \right. ; \left. 28,0\right)\)	27,0	16	0,32	32,0
\(\left[28,0 \right. ; \left. 30,0\right)\)	29,0	10	0,20	20,0
\(\left[30,0 \right. ; \left. 32,0\right)\)	31,0	4	0,08	8,0
\(\left[32,0 \right. ; \left. 34,0\right)\)	33,0	1	0,02	2,0
Total		50	1,00	100,0

Obtida a tabela de distribuição de frequências pode-se descrever o modelo de variação dos dados, através de uma análise superficial da distribuição dos dados. Observa-se, por exemplo, através da tabela acima que:

• 76,0% dos bezerros da raça nelore têm pesos ao nascer entre 24,0 e 30,0 kg (24,0 + 32,0 + 20,0);
• 14,0% estão abaixo de 24,0 kg (4,0 + 10,0);
• 10,0% estão acima de 30,0 kg (8,0 + 2,0).

As frequências acumuladas para baixo e para cima estão apresentadas nas Tabelas 2.11 e 2.12, respectivamente.

Tabela 2.11: Frequências acumuladas para baixo dos pesos ao nascer, em kg, de 50 bezerros da raça nelore, Fazenda XX, 2007.

Peso \(\mathbf{(kg)}\)	\(\mathbf{Fc\downarrow}\)
Menores que 20,0	0
Menores que 22,0	2
Menores que 24,0	7
Menores que 26,0	19
Menores que 28,0	35
Menores que 30,0	45
Menores que 32,0	49
Menores que 34,0	50

Por exemplo, menores que \(26,04\) kg: \(2 + 5 + 12 = 19\).

Tabela 2.12: Frequências acumuladas para cima dos pesos ao nascer, em kg, de 50 bezerros da raça nelore, Fazenda XX, 2007.

\(\mathbf{(kg)}\)	\(\mathbf{Fc\uparrow}\)
20,0 ou mais	50
22,0 ou mais	48
24,0 ou mais	43
26,0 ou mais	31
28,0 ou mais	15
30,0 ou mais	5
32,0 ou mais	1
34,0 ou mais	0

Por exemplo, \(28,0\) kg ou mais: \(10 + 4 + 1 = 15\).

2.3 Representação Gráfica

Num trabalho de descrição e apresentação de dados, os gráficos podem ser considerados como uma continuação das tabelas. A sua função é a de transmitir uma ideia visual do comportamento de um conjunto de dados. Para tal são utilizados diversos formatos gráficos de acordo com o problema a ser descrito, ou até mesmo de acordo com a preferência do apresentador. Os gráficos têm a vantagem de facilitar a compreensão do fenômeno em estudo que se queira descrever, permitindo a interpretação rápida das suas principais características.

2.3.1 Variáveis Qualitativas

No caso de variáveis qualitativas, nominal ou ordinal, existem vários tipos de gráficos para descrevê-las, mas apresentaremos apenas dois tipos: gráficos em de setores (pizza).

Considerando o Exemplo 2.2, os gráficos de barras e de setores para os dados estão representados nas Figuras 2.1 e 2.2, respectivamente.

Figura 2.1: Gráfico de barras para o nível de tecnificação adotado pelos produtores rurais, da região do Alto Rio Grande, sul de Minas Gerais, 2007.

Figura 2.2: Gráfico de setores para o nível de tecnificação adotado pelos produtores rurais, da região do Alto Rio Grande, sul de Minas Gerais, 2007.

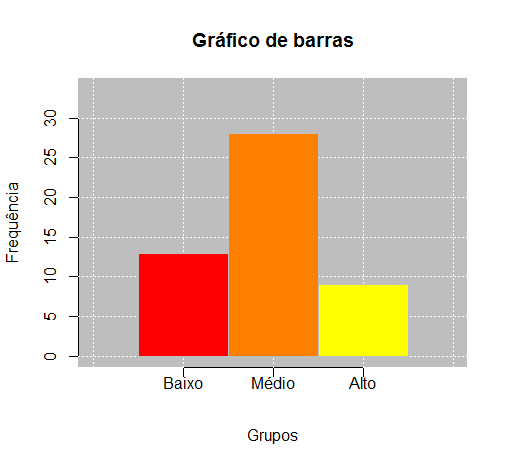
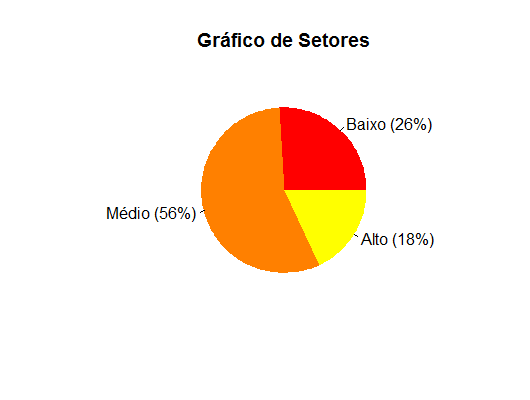
2.3.2 Variáveis Quantitativas

Para variáveis quantitativas, discretas ou contínuas, existem vários tipos de gráficos, mas abordaremos aqui os mais simples e utilizados.

2.3.2.1 Discretas

No caso de variáveis quantitativas discretas pode-se utilizar o gráfico de barras para descrevê-las.

Exemplo 2.5 Considerando o Exemplo 2.3, o gráfico de barras para os dados está representado pela Figura 2.3.

Figura 2.3: Gráfico de barras do número de pencas de banana maçã com empedramento, CEAGESP, São Paulo, SP, 2007.

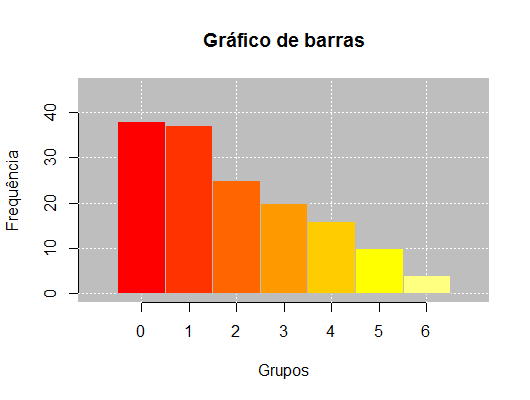
2.3.2.2 Contínuas

No caso de variáveis contínuas a tabela de distribuição de frequências pode ser representada graficamente através de:

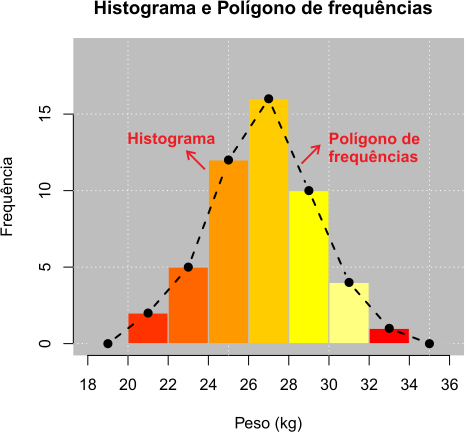
1. Histograma: Representa um gráfico formado por retângulos, cujas bases são proporcionais às amplitudes de classe, e as alturas proporcionais às frequências das classes. As frequências podem ser: absoluta \((F_i)\), relativa \((Fr_i)\) ou percentual \((Fp_i)\).

Características do histograma:

1. A área de um histograma é proporcional à soma das frequências;
2. Ao empregar as frequências relativas, obtém-se um gráfico de área unitária;
3. Para comparar duas distribuições de frequências, deve-se fazê-lo pelo histograma utilizando-se as frequências relativas ou percentuais.

2. Polígono de Frequências:

É um gráfico em linha. Para a construção do polígono de frequências, os pontos médios das classes nos topos do retângulos do histograma são unidos por linhas. O polígono começa e termina nos pontos médios das classes anterior à primeira e posterior à ultima, respectivamente.

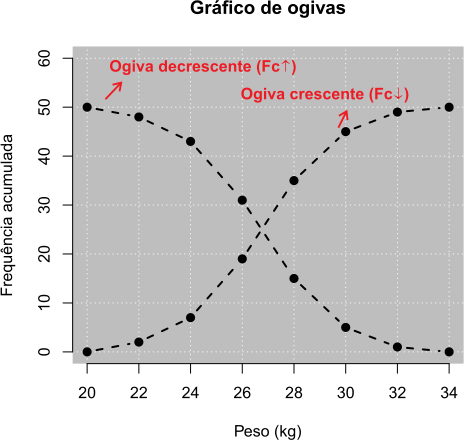
3. Ogivas:

É o polígono de frequências utilizando as frequências acumuladas para baixo ou para cima.

Exemplo 2.6 Para o Exemplo 2.4, tem-se o seguinte histograma e polígono de frequências para os dados, apresentados na Figura 2.4.

Figura 2.4: Histograma e polígono de frequências da distribuição dos pesos ao nascer, em kg, de \(50\) bezerros da raça nelore, Fazenda XX, 2007.

A Figura 2.5 apresenta o gráfico (ogivas) das frequências acumuladas para cima e para baixo.

Figura 2.5: Representação gráfica das distribuições acumuladas (ogivas) dos pesos ao nascer, em kg, de \(50\) bezerros da raça nelore, Fazenda XX, 2007.

2.4 Classificação da Distribuição dos Dados

No caso de variáveis quantitativas contínuas, a forma do polígono de frequências permite classificar a distribuição dos dados quanto a simetria em:

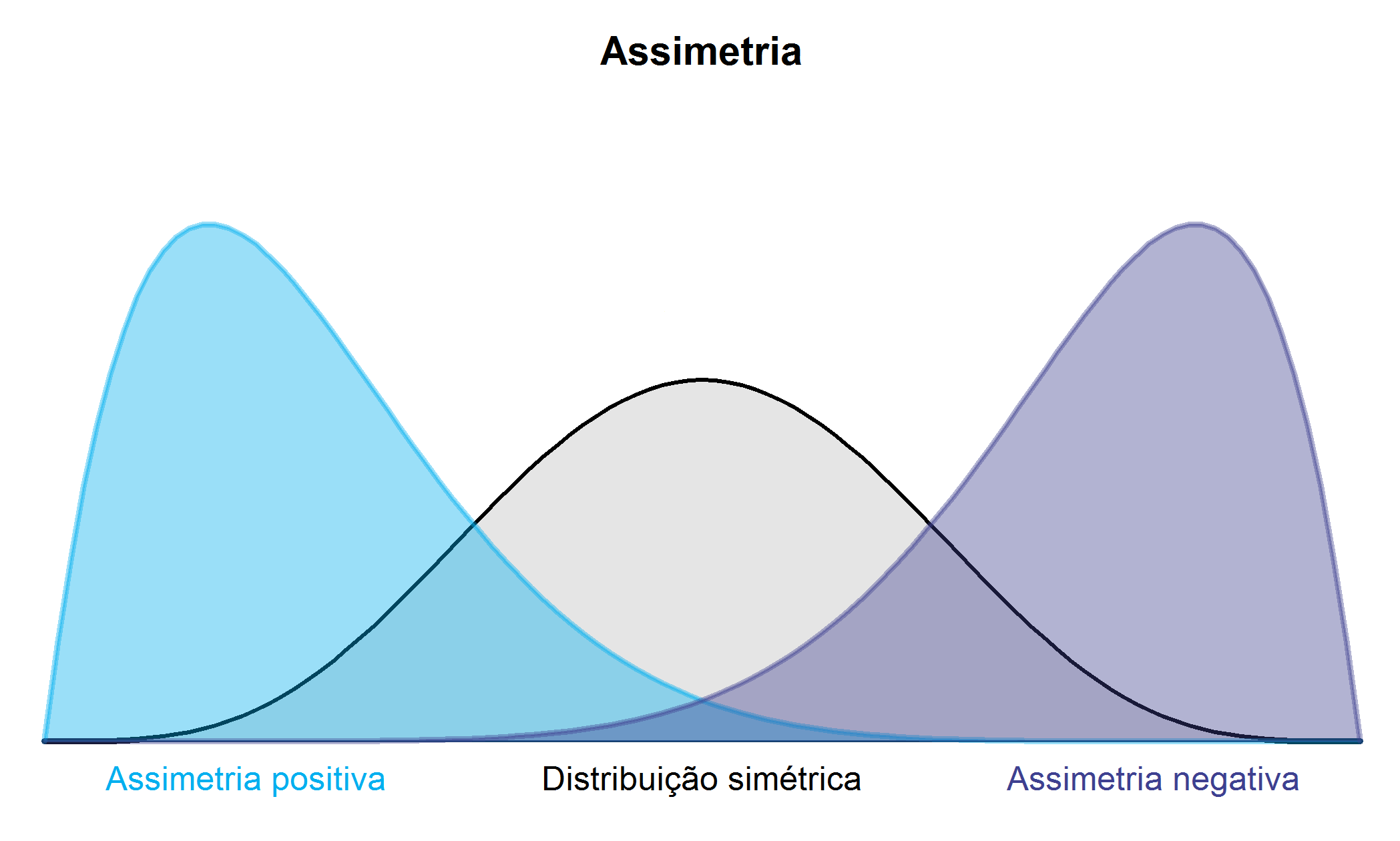
1. Simétrica;
2. Assimétrica à direita ou assimetria positiva;
3. Assimétrica à esquerda ou assimetria negativa.

Para tanto deve-se comparar a forma do Polígono de Frequências com as seguintes curvas, chamadas Curvas de Frequências, conforme Figura 2.6.

Figura 2.6: Classificação da simetria da distribuição dos dados.

Exemplo 2.7 No Exemplo 2.6, segundo a forma do polígono de frequência, a distribuição é simétrica.

2.5 Gráfico de Ramo e Folhas

Foi visto que a forma do polígono de frequências dá uma ideia da forma da distribuição da variável sob estudo. Um procedimento alternativo para resumir um conjunto de dados, com o objetivo de se obter uma ideia da forma de sua distribuição, é o gráfico de Ramo e Folhas. Uma vantagem deste diagrama é que não se perde, ou perde-se pouca informação sobre os dados em si.

Na construção do gráfico de Ramo e Folhas a ideia básica é dividir cada observação em duas partes: a primeira, chamada de ramo, é colocada à esquerda de uma linha vertical, e a segunda, a folha, é colocada à direita. No gráfico de Ramo e Folhas observa-se que um ramo com muitas folhas significa maior incidência daquele ramo.

Exemplo 2.8 Considerando o Exemplo 2.4, tem-se o seguinte gráfico de Ramo e Folhas, conforme Figura 2.7.

Figura 2.7: Pesos ao nascer, em kg, de 50 bezerros da raça nelore, Fazenda XX, 2007.

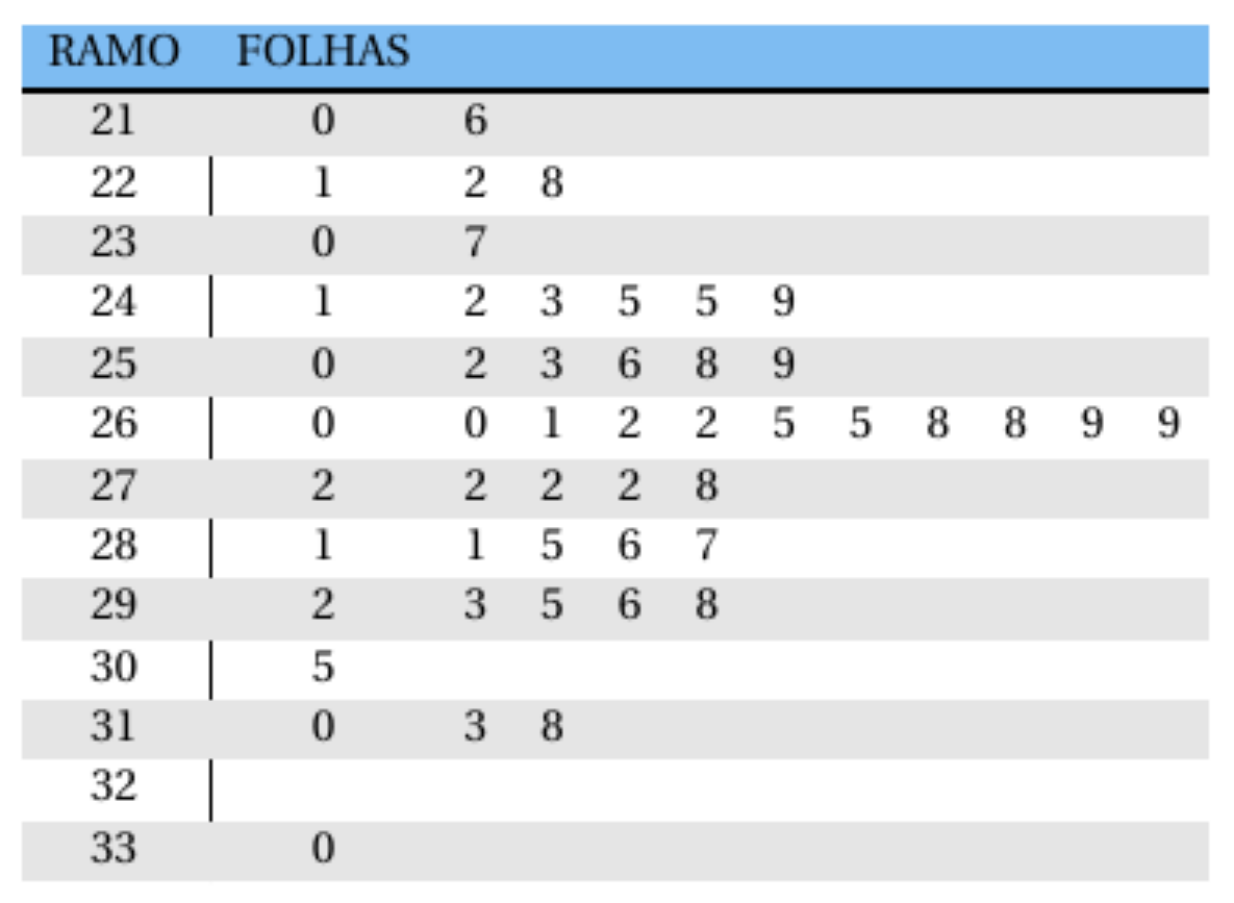
Por exemplo, para os pesos 21,0 e 21,6: o 21 é o ramo e o 0 e 6 são as folhas.

Algumas informações que se obtêm deste ramo-e-folhas são:

1. Os valores estão concentrados entre 24,1 e 29,8;
2. Um valor mais ou menos típico para este conjunto de dados poderia ser, por exemplo, 26,0;
3. A distribuição dos dados é simétrica.

2.6 Hipótese Tabular Básica

Nos cálculos estatísticos para dados de variáveis quantitativas contínuas, dispostas em uma tabela de distribuição de frequências com intervalos de classes, todos os dados contidos em uma determinada classe serão considerados iguais ao ponto médio da classe \(\tilde{X}_i\). Uma vez agrupada as observações nas classes, perde-se a informação individual de cada dado. Dessa forma, como será visto mais adiante, que não é possível o cálculo de medidas descritivas, como por exemplo, a média ou quaisquer outros tipos de medidas que dependam dos dados individualmente. Assim, a teoria da Hipótese Tabular Básica afirma que, usar o ponto médio para representar as observações de cada classe, representa o menor erro possível do que substituí-los por qualquer outro valor específico.

Exercícios propostos

Exercício 2.1 As distribuições das durações de alimentos em dois processos de conservação (A e B), em dias, estão representadas pelos histogramas, Figura 2.8.

Figura 2.8: Histograma do tempo de duração de alimentos, em dias, em dois processos de conservação de alimentos.

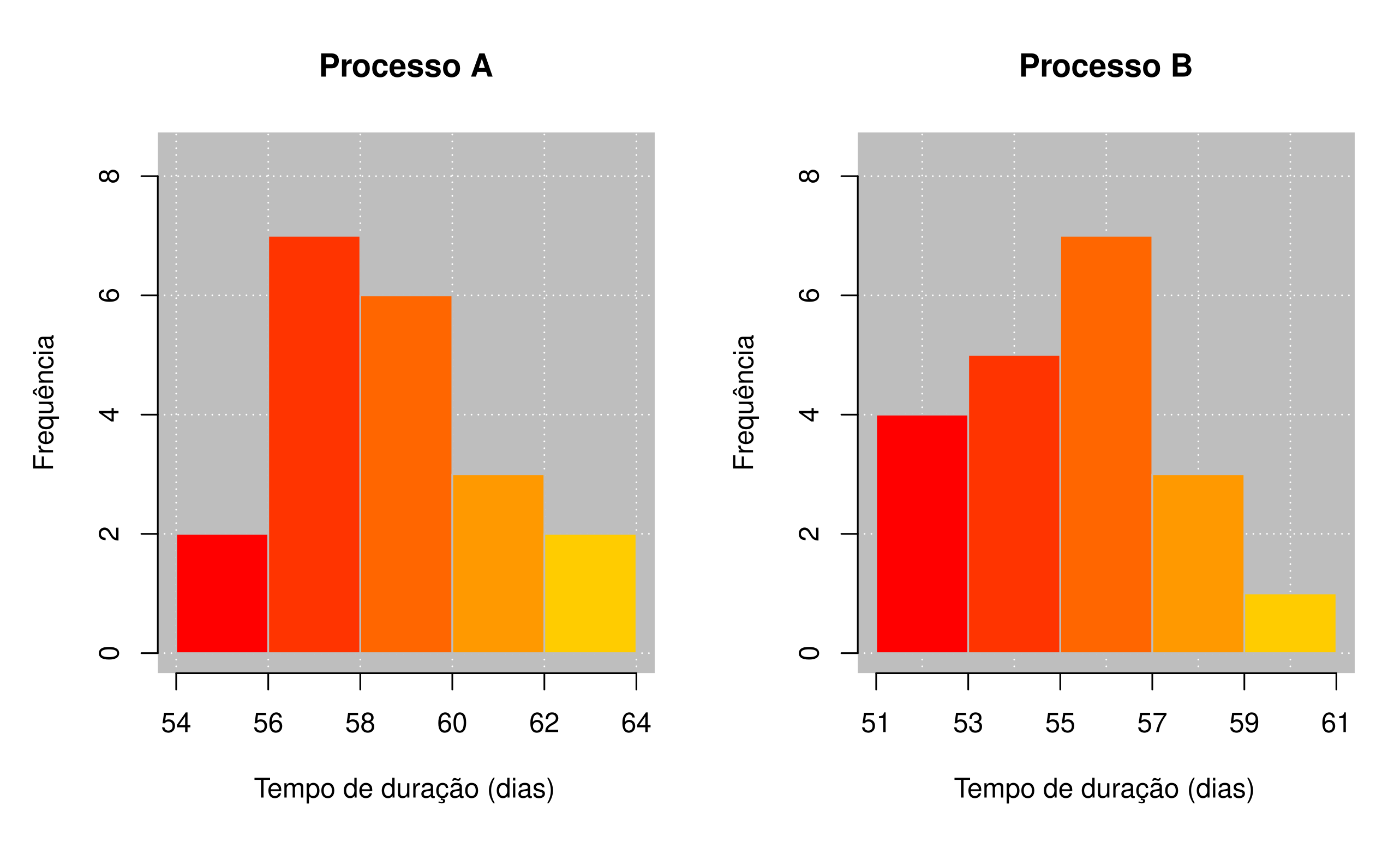
1. Classifique a distribuição dos dados dos dois processos de conservação de alimentos quanto à simetria.
2. No processo A qual a porcentagem de duração menor que 58 dias?
3. No processo B qual a proporção de duração de no mínimo 55 dias?
4. No processo A quantos duraram pelo menos 54 dias porém menos de 60 dias?

Exercício 2.2 Em um estudo referente as atividades predominantes em 20 propriedades de um município, observou-se as seguintes atividades:

Café	Feijão	Café	Soja
Café	Milho	Feijão	Milho
Milho	Milho	Soja	Soja
Leite	Leite	Milho	Café

1. Classifique a variável;
2. Construa uma tabela de distribuição de frequências com as frequências: absoluta, relativa e percentual;
3. Faça a representação gráfica por meio dos gráficos de colunas e de setores;
4. Qual a porcentagem de propriedades que cultivam predominantemente café em suas propriedades.

Exercício 2.3 Os dados a seguir referem-se a produção diária de leite, em litros, de 20 vacas da raça holandesa, de um rebanho pertencente ao Núcleo de Criadores de Gado Holandês do Sul de Minas Gerais.

20,6	16,2	26,6	22,2	14,4
18,4	20,6	23,4	22,0	15,8
25,2	21,8	20,8	19,2	18,4
14,2	27,0	21,4	20,6	16,2

1. Classifique a variável;
2. Construa uma tabela de distribuição de frequências com as frequências: absoluta, relativa e percentual;
3. Construa o histograma e o polígono de frequências;
4. Obtenha as distribuições de frequência acumuladas para cima e para baixo;
5. Classifique a distribuição quanto à simetria;
6. Construa o gráfico de Ramo e Folhas.

Exercício 2.4 Considere os dados da seguinte tabela de distribuição de frequências, apresentados na Tabela 2.13.

Tabela 2.13: Área, em ha, de 755 propriedades rurais de um município do Estado de Minas Gerais, 2007.⁵

Área \(\mathbf{(ha)}\)	\(\mathbf{F_i}\)
Abaixo de 60,0	386
\(\left[60,0 \right. ; \left. 150,0 \right)\)	237
\(\left[150,0 \right. ; \left. 250,0 \right)\)	62
\(\left[250,0 \right. ; \left. 400,0 \right)\)	43
\(\left[400,0 \right. ; \left. 600,0 \right)\)	18
\(\left[600,0 \right. ; \left. 900,0 \right)\)	7
900,0 ou mais	2
Total	755

1. Quantas propriedades têm área abaixo de 120 ha;
2. Qual a porcentagem de propriedades com área acima de 300 ha.

Exercício 2.5 Para estudar a produtividade de um canavial, demarcaram-se nele em vários pontos escolhidos ao acaso, 50 pequenas áreas de 100 \(\textrm{m}^2\) cada, cuja produção foi pesada. Os resultados obtidos, em kg, estão apresentados na seguinte tabela de distribuição de frequências:

Tabela 2.14: Produção de cana-de-açúcar, em kg, por áreas de 100 \(\textrm{m}^2\) de um canavial, Fazenda XX, 2007.⁶

Produção \(\mathbf{(kg)}\)	\(\mathbf{\tilde{X}_i}\)	\(\mathbf{F_i}\)	\(\mathbf{Fr_i}\)	\(\mathbf{Fp_i(\%)}\)
\(\left[624,0 \right. ; \left. \rule{10mm}{.2pt}\right)\)	\(\rule{10mm}{.2pt}\)	\(\rule{10mm}{.2pt}\)	0,02	\(\rule{10mm}{.2pt}\)
\(\left[\rule{10mm}{.2pt} \right. ; \left. \rule{10mm}{.2pt}\right)\)	\(\rule{10mm}{.2pt}\)	\(\rule{10mm}{.2pt}\)	\(\rule{10mm}{.2pt}\)	10,0
\(\left[\rule{10mm}{.2pt} \right. ; \left. \rule{10mm}{.2pt}\right)\)	\(\rule{10mm}{.2pt}\)	\(\rule{10mm}{.2pt}\)	\(\rule{10mm}{.2pt}\)	\(\rule{10mm}{.2pt}\)
\(\left[\rule{10mm}{.2pt} \right. ; \left. \rule{10mm}{.2pt}\right)\)	\(\rule{10mm}{.2pt}\)	13	\(\rule{10mm}{.2pt}\)	\(\rule{10mm}{.2pt}\)
\(\left[\rule{10mm}{.2pt} \right. ; \left. \rule{10mm}{.2pt}\right)\)	\(\rule{10mm}{.2pt}\)	7	\(\rule{10mm}{.2pt}\)	\(\rule{10mm}{.2pt}\)
\(\left[\rule{10mm}{.2pt} \right. ; \left.\rule{10mm}{.2pt}\right)\)	\(\rule{10mm}{.2pt}\)	\(\rule{10mm}{.2pt}\)	0,10	\(\rule{10mm}{.2pt}\)
\(\left[\rule{10mm}{.2pt} \right. ; \left.\rule{10mm}{.2pt}\right)\)	\(\rule{10mm}{.2pt}\)	3	\(\rule{10mm}{.2pt}\)	\(\rule{10mm}{.2pt}\)
\(\left[\rule{10mm}{.2pt} \right. ; \left. \rule{10mm}{.2pt}\right)\)	\(\rule{10mm}{.2pt}\)	\(\rule{10mm}{.2pt}\)	\(\rule{10mm}{.2pt}\)	2,0
Total		\(\rule{10mm}{.2pt}\)	\(\rule{10mm}{.2pt}\)	\(\rule{10mm}{.2pt}\)

1. Complete a tabela de distribuição de frequências considerando que a maior observação foi 954,0 kg;
2. Construa o histograma e o polígono de frequências e classifique a distribuição dos dados quanto à simetria;
3. Qual a porcentagem de áreas de 100 \(\textrm{m}^2\) avaliadas produziram menos de 844,0 kg de cana-de-açúcar;
4. Qual a proporção de áreas de 100 \(\textrm{m}^2\) avaliadas produziram no mínimo 800,0 kg de cana-de-açúcar;
5. Quantas áreas de 100 \(\textrm{m}^2\) avaliadas produziram pelo menos 712,0 kg, porém menos de 888,0 kg de cana-de-açúcar.

BANZATTO, D. A.; NASCIMENTO KRONKA, S. DO. Experimentação Agrícola. Jaboticabal: Funep, 2006. p. 237

BARBIN, D. Planejamento e Análise Estatística de Experimentos Agrômica. Arapongas: Midas, 2003. p. 208

BOLFARINE, H.; BUSSAB, W. O. Elementos de Amostragem. São Paulo: Edgard Blucher, 2005. p. 274

BOLFARINE, H.; SANDOVAL, M. C. Introdução à Inferência Estatística. 2. ed. São Paulo: SBM, 2010. p. 159

COCHRAN, W.; COX, G. M. Experimental Designs. 2. ed. New York: John Wiley & Sons, 2005. p. 618

CRESPO, A. A. Estatística Fácil. 19. ed. São Paulo: Saraiva, 2009. p. 232

DANTAS, C. A. B. Probabilidade: Um Curso Introdutório. 3. ed. São Paulo: EDUSP, 2008. p. 256

DRAPER, N. R.; SMITH, H. Applied regression analysis. 3. ed. New York: Wiley, 1998. p. 736

MAGALHAES, M. N. Probabilidade e variáveis aleatórias. 3. ed. São Paulo: EDUSP, 2011. p. 424

MAGALHAES, M. N.; LIMA, A. C. P. Noções de Probabilidade e Estatística. 7. ed. São Paulo: EDUSP, 2023. p. 428

MEYER, P. L. Probabilidade: aplicações á estatística. 2. ed. Rio de Janeiro: LTC, 2000. p. 426

MONTGOMERY, D. C. Design and Analysis of Experiments. 9. ed. New Jersey: Wiley, 2019. p. 752

MONTGOMERY, D. C.; RUNGER, G. C. Estatísta Aplicada e Probabilidade para Engenheiros. 7. ed. Rio de Janeiro: LTC, 2021. p. 416

MOOD, A. M.; GRAYBILL, F. A.; BOES, D. C. Introduction to the Theory of Statistics. New York: John Wiley & Sons, 1974. p. 564

PAGANO, M.; GAUVREAU, K. Princípios de Bioestatística. São Paulo: Thomson, 2004. p. 506

PIMENTEL-GOMES, F. Curso de Estatística Experimental. 15. ed. Piracicaba: FEALQ, 2022. p. 451

SILVA, N. N. Amostragem Probabilística. 3. ed. São Paulo: EDUSP, 2015. p. 136

SOUZA, G. S. Introdução aos Modelos de Regressão Linear e Não-Linear. Brasília: EMBRAPA, 1998. p. 489

STEEL, R. G. D.; TORRIE, J. H. Principles and procedures of statistics: A biometrical approach. 2. ed. New York: McGraw-Hill Book Company, 1980. p. 512

---

1. Também pode ser chamada de tabela de distribuição com dados agrupados sem intervalo de classes.

2. Fonte: Dados fictícios.

3. Fonte: Dados fictícios.

4. Fonte: Dados fictícios.

5. Fonte: Dados fictícios.

6. Fonte: Dados fictícios.