9 Teoria da Estimação
9.1 Introdução
Toda população é descrita por um certo modelo probabilístico \(f(x | \theta)\), com parâmetro(s) \(\theta\) desconhecido(s), e o interesse é obter algum tipo de informação acerca desse(s) parâmetro(s). O que se dispõe é de uma amostra, ou seja, de partes de elementos da população. A partir de uma amostra aleatória é possível obter aproximações numéricas para o(s) parâmetro(s) \(\theta\) do modelo, e esse processo é chamado estimação. Assim, um dos objetivos da Estatística é obter informações sobre os parâmetros populacionais através das estimativas amostrais.
9.2 Conceitos Básicos
Para formalizar as ideias que serão apresentadas alguns conceitos são úteis.
9.2.1 Parâmetro
Um parâmetro é um valor desconhecido associado a uma característica da população, e em geral representado por letras gregas.
Exemplo 9.1 A média \(\mu\) e a variância \(\sigma^2\) de uma população são parâmetros.
9.2.2 Estimador
O estimador é a função ou expressão algébrica que estima o valor de um parâmetro populacional, baseando-se nas observações de uma amostra aleatória.
Exemplo 9.2
- \(\bar{x}=\frac{\sum_{i=1}^{n}x_i}{n}\) é um estimador da média populacional \(\mu\);
- \(s^2=\frac{\sum_{i=1}^{n}x_i^2-\frac{\left(\sum_{i=1}^{n}x_i\right)^2}{n}}{n-1}\) é um estimador da variância populacional \(\sigma^2\).
9.2.3 Estimativa
Uma estimativa é uma aproximação numérica para um parâmetro associado a um modelo probabilístico, ou seja, é o valor obtido pelo estimador numa determinada amostra aleatória.
Exemplo 9.3 Numa certa variedade de milho tem-se uma estimativa da altura média desta variedade, dada por:
\[ \bar{x}=200,0~\textrm{cm}. \]
9.3 Tipos de Estimativas
Basicamente existem dois processos de estimação. O primeiro deles é a chamada estimação pontual, pela qual um valor numérico é obtido através de um estimador, como sendo uma aproximação numérica para o parâmetro populacional.
Exemplo 9.4 Numa amostra aleatória de n elementos os valores de \(\bar{x}\) e \(s^2\) estimam \(\mu\) e \(\sigma^2\), respectivamente, por ponto.
Exemplo 9.5 Seja uma amostra de 40 plantas de uma variedade de milho, em que a variável altura, apresentou uma média de \(200,0\) cm e um desvio padrão de \(10,0\) cm.
Nesta amostra a média amostral, \(\bar{x}=200,0\) cm, é uma estimativa por ponto da média populacional \(\mu\), e o desvio padrão amostral, \(s = 10,0\) cm, é uma estimativa por ponto do desvio padrão populacional \(\sigma\).
O segundo processo de estimação é a estimação por intervalo, no qual algum tipo de intervalo é construído, de tal maneira que se possa atribuir probabilidades de que o valor real do parâmetro esteja ali contido. Neste caso, o parâmetro populacional é estimado por dois valores, obtidos através de cálculos com os dados amostrais, que formam um intervalo, dentro do qual se espera encontrar o verdadeiro valor do parâmetro. A vantagem desse processo é que mostra a precisão da estimativa.
Exemplo 9.6 Considerando o exemplo anterior tem-se que a expressão: \[ IC_{95,0\%}(\mu):~[196,90~\textrm{cm};~ 203,10~\textrm{cm}], \] é uma estimativa por intervalo para \(\mu\) com uma confiança de 95,0% e um erro de 3,10 cm.
Assim, a associação entre estimativas pontuais acerca de um parâmetro populacional, e o conhecimento de probabilidades de que o parâmetro esteja contido em certos intervalos, possibilitará, em geral, promover uma inferência informativa a respeito do parâmetro desconhecido.
9.4 Métodos de Estimação Pontual
Os métodos de obtenção de estimativas pontuais, os quais não serão discutidos em detalhes aqui, são:
- Método dos Momentos;
- Método dos Quadrados Mínimos;
- Método da Máxima Verossimilhança.
9.5 Propriedades dos Estimadores Pontuais
Em função da existência de vários métodos para estimação de parâmetros, é importante analisar algumas propriedades dos estimadores, que possa auxiliar na escolha de um estimador para um parâmetro em particular. Essas propriedades são:
- Vício: Um estimador \(\hat{\theta}\) de um parâmetro \(\theta\) é não viciado, ou não tendencioso, ou não viesado, se: \[ E(\hat{\theta})=\theta. \]
Exemplo 9.7 A média amostral, \(\bar{x} = \sum_{i = 1}^{n}x_i / n\), é um estimador não viciado da média populacional \(\mu\), pois pode-se provar que:
\[ E(\bar{x})=\mu. \]
Ou seja, um estimador é não viciado se o seu valor esperado coincide com o parâmetro de interesse.
Exemplo 9.8 A variância amostral, \(\hat{\sigma}^2 = \sum_{i = 1}^{n}(x_i - \bar{x})^2 / n\), é um estimador viciado para \(\sigma^2\).
Pode ser demonstrado que:
\[ E(\hat{\sigma}^2)=\left(\frac{n-1}{n}\right) \sigma^2. \]
Por outro lado tem-se que: \[ E\left(\frac{n}{n-1}\hat{\sigma}^2\right)=\sigma^2 \] Note que:
\[ \left(\frac{n}{n-1}\hat{\sigma}^2\right)=\left(\frac{n}{n-1}\right)\frac{\sum_{i=1}^{n}\left(x_i- \bar{x} \right)^2}{n}=\frac{1}{n-1}\sum_{i=1}^{n}\left(x_i- \bar{x} \right)^2=s^2. \]
Logo, \(s^2\) é um estimador não viciado para \(\sigma^2\).
- Consistência: Um estimador \(\hat{\theta}\) é consistente se à medida que o tamanho n da amostra aumenta, seu valor esperado converge para o parâmetro de interesse, e sua variância converge para zero. Ou seja, \(\hat{\theta}\) é consistente se as duas propriedades são satisfeitas:
- \(\lim_{n \to \infty} E(\hat{\theta}) = \theta\);
- \(\lim_{n \to \infty} V(\hat{\theta}) = 0\).
- Eficiência: Dados dois estimadores \(\hat{\theta}_1\) e \(\hat{\theta}_2\), não viciados para um parâmetro \(\theta\), diz-se que \(\hat{\theta}_1\) é mais eficiente que \(\hat{\theta}_2\) se: \(V(\hat{\theta}_1)\) < \(V(\hat{\theta}_2)\). Isto é, dentre todos os estimadores não viciados de um parâmetro \(\theta\), aquele que tiver menor variância é o estimador mais eficiente de \(\theta\).
Exemplo 9.9 Numa amostra a média amostral \(\bar{x}\) é um estimador mais eficiente da média populacional \(\mu\) que a mediana \(md\), pois pode-se provar que: \[ V(\bar{x})=\frac{\sigma^2}{n}~\textrm{e}~ V(md)=\frac{\pi}{2}\times \frac{\sigma^2}{n}. \]
Logo \(V(\bar{\text{x}}) < V(md)\).
No caso de uma estimativa por intervalo, o comprimento do intervalo de confiança dá uma idéia da eficiência da estimativa.
9.6 Estimação por intervalo
Os estimadores pontuais fornecem como estimativa um único valor numérico para o parâmetro \(\theta\) de interesse, associado ao modelo probabilístico \(f(x | \theta)\). A inferência pode e deve ser complementada, sempre que possível, com pressuposições acerca de probabilidades de \(\theta\) estarem próximos ou não de suas estimativas pontuais. Por serem variáveis aleatórias, os estimadores possuem uma distribuição de probabilidade, e levando este fato em consideração, pode-se apresentar uma estimativa mais informativa para o parâmetro de interesse, que inclua uma medida de precisão do valor obtido. Este método de estimação, denominado estimação por intervalo, incorpora à estimativa pontual do parâmetro, informações a respeito de sua variabilidade, permitindo a construção de intervalos com probabilidades conhecidas de que o valor paramétrico esteja contido nesse intervalo.
Assim, intervalos de confiança são obtidos através da distribuição amostral de seus estimadores.
Seja \(x_1\), \(x_2\), \(\cdots\), \(x_n\) uma amostra aleatória coletada numa população descrita pelo modelo probabilístico \(f(x | \theta)\). Sejam \(T_1(x)\) e \(T_2(x)\) duas estatísticas que satisfaçam: \(T_1(x) < T_2(x)\), e também que: \(P[T_1(x) < \theta < T_2(x)]=1 - \alpha\).
O intervalo aleatório: \([T_1(x); T_2(x)]\) é chamado de intervalo de confiança para \(\theta\) com \((1 - \alpha)100,0\%\) de probabilidade. A probabilidade \((1 - \alpha)\) é chamada coeficiente de confiança do intervalo. O comprimento do intervalo de confiança é dado por: \[\begin{align*} L(x)=T_2(x) - T_1(x). \end{align*}\]
Logo, a construção de intervalos de confiança consiste na obtenção de \(T_1(x)\) e \(T_2(x)\).
9.7 Construção de Intervalos de Confiança
Basicamente os intervalos de confiança podem ser construídos utilizando a distribuição de quantidades pivotais.
Considere uma amostra aleatória \(x_1\), \(x_2\), \(\cdots\), \(x_n\) de uma população descrita pelo modelo probabilístico \(f(x | \theta)\). Uma função \(g(x; \theta)\), cuja distribuição não dependa de \(\theta\), é chamada de quantidade pivotal.
Exemplo 9.10 Considere um modelo probabilístico correspondente a uma distribuição normal de média \(\mu\) e variância \(\sigma^2\). Seja, \[ Z=\frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt{n}}}. \]
Neste caso é \(Z\) uma quantidade pivotal, pois \(Z\) é uma variável aleatória com distribuição normal padronizada, ou seja, \(Z\sim N(0,0; 1,0)\), e não depende de \(\mu\) e \(\sigma^2\).
Nas próximas seções, serão utilizados as distribuições de probabilidades e resultados, vistos no Capítulo 8, para a construção de intervalos de confiança para parâmetros populacionais de interesse.
9.7.1 Intervalo de Confiança para a Média de uma Distribuição Normal
A média estimada a partir de uma amostra aleatória, é apenas uma estimativa por ponto da verdadeira média populacional \(\mu\). A média verdadeira é um parâmetro que na grande maioria das vezes é desconhecida. Entretanto, a partir do conhecimento das distribuições teóricas de \(Z\) e \(t\), pode-se construir um intervalo que deve conter a verdadeira média populacional \(\mu\).
Para a construção do intervalo de confiança para a média, tem-se as seguintes situações, descritas a seguir.
9.7.1.1 Grandes Amostras ou Variância Populacional Conhecida
O intervalo de confiança associado a um determinado nível de confiança, para a média populacional \(\mu\), quando se tem grandes amostras \((n\geq 30)\), ou variância populacional \(\sigma^2\) conhecida, pode ser deduzido da seguinte forma.
Foi visto no capítulo anterior de acordo com o teorema central do limite que: \[ \bar{\text{x}} \sim N\left(\mu, \frac{\sigma^2}{n} \right) \]
Logo, na distribuição de \(\bar{x}\) o valor de \(Z\) é obtido por: \[ Z=\frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt{n}}}, \tag{9.1}\] em que \(Z \sim N(0,0; 1,0)\).
Na distribuição de \(\bar{x}\) pode-se esquematizar uma probabilidade de \((1 - \alpha)\), conforme Figura 9.1.
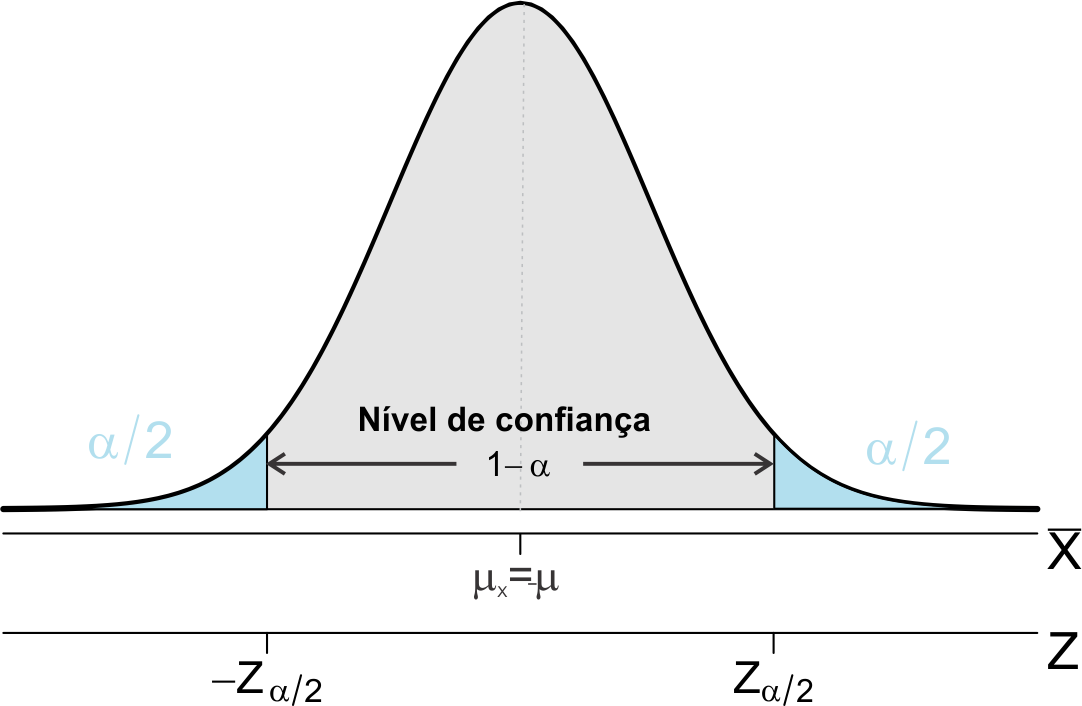
Logo, \[ P\left[-Z_\frac{\alpha}{2} < Z < Z_\frac{\alpha}{2} \right]=1 - \alpha. \tag{9.2}\]
Substituindo (9.1) em (9.2), tem-se: \[ P\left[-Z_\frac{\alpha}{2} < \frac{\bar{\text{x}}-\mu}{\frac{\sigma}{\sqrt{n}}} < Z_\frac{\alpha}{2} \right]=1 - \alpha. \]
Multiplicando cada termo da desigualdade por: \(\frac{\sigma}{\sqrt{n}}\), obtém-se: \[ P\left[-Z_\frac{\alpha}{2}\times\frac{\sigma}{\sqrt{n}} < \bar{\text{x}}-\mu < Z_\frac{\alpha}{2}\times \frac{\sigma}{\sqrt{n}} \right]=1 - \alpha. \]
Subtraindo \(\bar{x}\) de cada termo da desigualdade a expressão fica: \[ P\left[-\bar{\text{x}}-Z_\frac{\alpha}{2}\times\frac{\sigma}{\sqrt{n}} < -\mu < -\bar{\text{x}}+Z_\frac{\alpha}{2}\times\frac{\sigma}{\sqrt{n}} \right]=1 - \alpha. \]
Multiplicando cada termo da desigualdade por (-1), tem-se: \[ P\left[\bar{\text{x}}+Z_\frac{\alpha}{2}\times\frac{\sigma}{\sqrt{n}} > \mu > \bar{\text{x}}-Z_\frac{\alpha}{2}\times\frac{\sigma}{\sqrt{n}} \right]=1 - \alpha. \]
Invertendo os extremos do intervalo obtém-se a expressão (9.3), para a construção do intervalo de confiança para \(\mu\) com \((1 - \alpha)100,0\%\) de probabilidade. \[ P\left[\bar{x}-Z_\frac{\alpha}{2}\times\frac{\sigma}{\sqrt{n}} < \mu < \bar{x}+Z_\frac{\alpha}{2}\times\frac{\sigma}{\sqrt{n}} \right]=1 - \alpha, \tag{9.3}\] em que:
- \(\bar{x} \pm Z_\frac{\alpha}{2}\times\frac{\sigma}{\sqrt{n}}\) são os limites de confiança;
- \((1 - \alpha)100,0\%\) é o grau ou nível de confiança.
A representação gráfica de (9.3) pode ser observada na Figura 9.2.
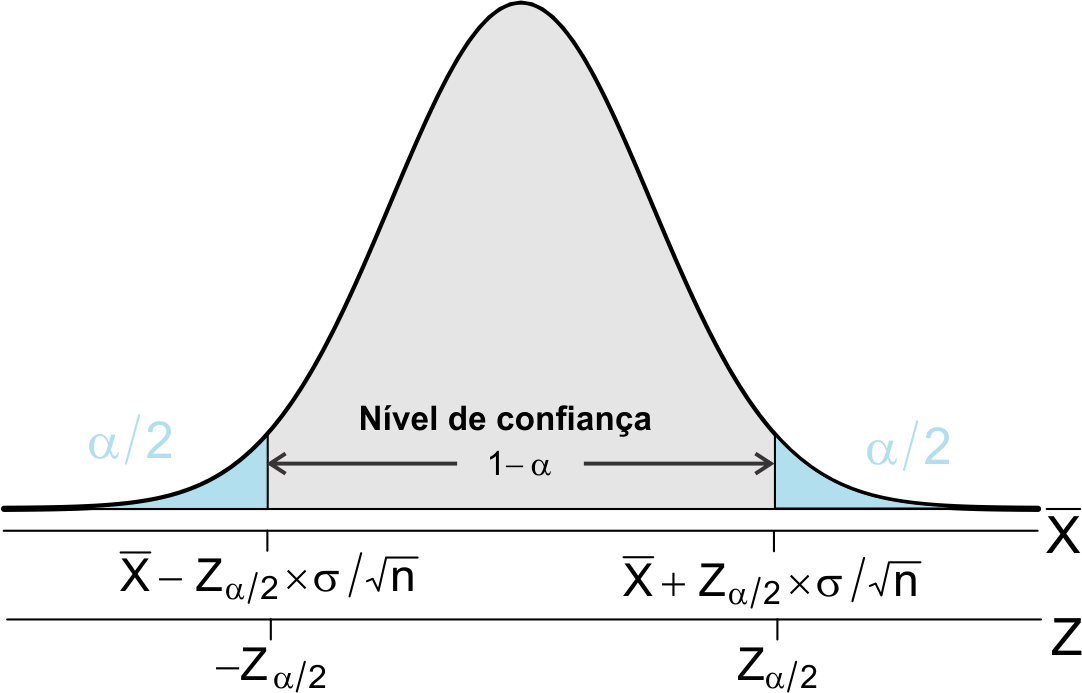
Não conhecendo-se o valor de \(\sigma\) (desvio padrão populacional), pode-se usar o valor de \(s\) (desvio padrão amostral), desde que \(n\geq 30\).
Exemplo 9.11 Seja uma amostra de 40 plantas de uma variedade de milho, em que a variável altura, apresentou uma média de 200,0 cm e variância de 100,0 cm\(^2\). Construir um intervalo de confiança de 95,0% para a média populacional \(\mu\). Neste caso, não se conhece a variância populacional \(\sigma^2\), e sim, a variância amostral \(s^2\). Como o tamanho da amostra é n = 40, considera-se razoável a utilização do desvio padrão amostral. Para construir um intervalo de confiança de 95,0% para a média populacional \(\mu\), tem-se:
- \(n=40\);
- \(\bar{\text{x}}=200,0\) cm;
- \(s^2=100,0\) cm\(^2 \Rightarrow s=\sqrt{100,0}=10,0\) cm;
- \((1 - \alpha)=0,95 \Rightarrow \alpha=0,05 \Rightarrow \frac{\alpha}{2}=0,025\). \[ Z_\frac{\alpha}{2}=Z_{0,025}=? \]
Consultando a Tabela A 1, tem-se que o valor de Z que deixa uma probabilidade acima dele de 0,025 é igual a 1,96. Dentro do corpo da tabela consulta-se o valor referente a 0,025, conforme esquema abaixo.
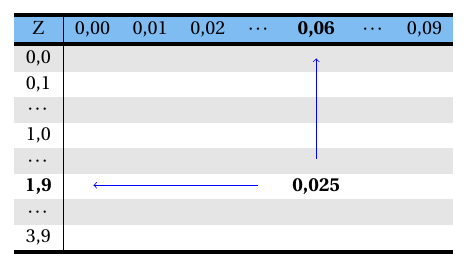
Logo, \[ Z_{0,025}=1,96. \]
Através da expressão (9.3), tem-se que: \[ 200,0-1,96\frac{10}{\sqrt{40}} < \mu < 200,0+1,96\frac{10}{\sqrt{40}} \] \[ 200,0 - 3,10 < \mu < 200,0 + 3,10 \] \[ \Rightarrow IC_{0,95}(\mu): [196,90~\textrm{cm}; 203,10~\textrm{cm}]. \]
Esse resultado mostra que é de 95,0% a confiança, da verdadeira altura média das plantas de milho estar entre 196,90 e 203,10 cm. Do ponto de vista de amostragem isto quer dizer que, se forem retiradas várias amostras aleatórias dentro desta população, calculando-se os valores de \(\bar{x}\) e \(s\) para cada amostra, e construindo o intervalo de confiança para \(\mu\) em cada amostra, 95,0% dos intervalos conterão em seu interior o verdadeiro valor da média populacional \(\mu\).
Exemplo 9.12 Considerando o Exemplo 9.11, construir um intervalo de confiança de 99,0% para a média populacional \(\mu\).
Assim, tem-se: \[ (1 - \alpha)=0,99 \Rightarrow \alpha=0,01 \Rightarrow \frac{\alpha}{2}=0,005. \] \[ Z_\frac{\alpha}{2}=Z_{0,005}=? \]
Consultando a Tabela A 1, o valor de Z que deixa uma probabilidade acima dele de 0,005 (média de 0,0051 e 0,0049) é igual a 2,575 ( média de 2,57 e 2,58). Dentro do corpo da tabela consulta-se o valor referente a 0,005 ou mais próximo, conforme esquema abaixo:
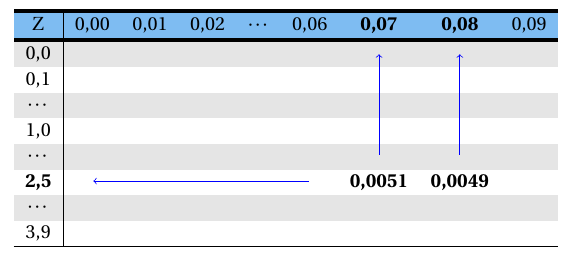
Logo, \[ Z_{0,005}=2,575. \] Através da expressão (9.3), tem-se que: \[ 200,0-2,575\frac{10}{\sqrt{40}} < \mu < 200,0+2,575\frac{10}{\sqrt{40}} \] \[ 200,0 - 4,07 < \mu < 200,0 + 4,07 \] \[ \Rightarrow IC_{0,99}(\mu): [195,93~\textrm{cm}; 204,07~\textrm{cm}]. \]
Esse resultado mostra que é de 99,0% a confiança, da verdadeira altura média das plantas de milho estar entre 195,93 e 204,07 cm.
O erro da estimativa é dado pela expressão (9.4). \[ e=\bar{\text{x}} - \mu. \tag{9.4}\]
O erro máximo da estimativa na construção do intervalo de confiança é dado pela expressão (9.5). \[ e=Z_\frac{\alpha}{2}\frac{\sigma}{\sqrt{n}}. \tag{9.5}\]
Exemplo 9.13 Nos Exemplos 9.11 e 9.12, tem-se que:
- \(\alpha=5,0\%=0,05 \Rightarrow e=3,10\) cm, ou seja, com 95,0% de confiança, a média, \(\bar{\text{x}}=200,0\) cm, estima a média populacional \(\mu\) com um erro máximo de 3,10 cm;
- \(\alpha=1,0\%=0,01 \Rightarrow e=4,07\) cm, ou seja, com 99,0% de confiança, a média, \(\bar{\text{x}}=200,0\) cm, estima a média populacional \(\mu\) com um erro máximo de 4,07 cm.
As consequências da redução de \(\alpha\) são: - O coeficiente de confiança \((1 - \alpha)100,0\%\) aumenta: \[ 95,0\% \Rightarrow 99,0\%. \]
- O erro da estimativa aumenta:
\[ 3,10~\textrm{cm}~\Rightarrow~4,07~\textrm{cm}. \]
- O comprimento do intervalo de confiança aumenta: \[ [196,9~\textrm{cm};~203,10~\textrm{cm}]~\Rightarrow~ [195,93~\textrm{cm};~204,07~\textrm{cm}]. \]
Tem-se que, a única forma de aumentar a confiança e reduzir o comprimento do intervalo, simultaneamente, é aumentando o tamanho da amostra.
A partir do intervalo de confiança para a média \(\mu\), pode-se dimensionar o tamanho da amostra estatisticamente para estimar a média \(\mu\).
Na abordagem estatística considerada para determinar o tamanho da amostra, o nível de precisão e o erro da estimativa são especificados antecipadamente.
A expressão do erro máximo é dada por. \[ e=Z_\frac{\alpha}{2}\frac{\sigma}{\sqrt{n}}. \tag{9.6}\]
Isolando \(n\) em (9.6), obtém-se a expressão (9.7) para dimensionar o tamanho da amostra estatisticamente. \[ n=\left(\frac{Z_\frac{\alpha}{2}\sigma}{e} \right)^2. \tag{9.7}\]
Exemplo 9.14 No Exemplo 9.11, tem-se que:
- n=40;
- \(\bar{\text{x}}=200,0\) cm;
- \(s=10,0\) cm;
- \(\alpha=5,0\%=0,05\);
- \(e=3,10\) cm.
Quantas plantas deverão ser examinadas num próximo estudo, para estimar \(\mu\) com um erro de 2,8 cm e uma confiança de 95,0%?
Neste caso, tem-se que:
- \(e=2,8\) cm;
- \(\alpha=0,05 \Rightarrow \frac{\alpha}{2}=0,025\);
- \(Z_{0,025}=1,96\).
Logo, através da expressão (9.7), tem-se que:
\[ n=\left(\frac{1,96(10,0)}{2,8}\right)^2=49~\textrm{plantas}. \]
9.7.1.2 Pequenas Amostras e Variância Populacional Desconhecida
Geralmente não se conhece o valor da variância populacional \(\sigma^2\). Foi visto que a variância populacional \(\sigma^2\) pode ser estimada a partir da variância amostral \(s^2\). Assim, é possível construir um intervalo de confiança de \((1 – \alpha)100,0\%\) para a média populacional \(\mu\), utilizando a distribuição \(t\) em lugar de \(Z\). Deste modo, é possível obter o intervalo de confiança para pequenas amostras, \((n < 30)\), quando somente a variância amostral \(s^2\) é conhecida.
Nesse caso, utiliza-se da distribuição da variável \(t\), dada por: \[ t=\frac{\bar{x}-\mu}{\frac{s}{\sqrt{n}}}, \tag{9.8}\] em que \(t\) segue uma distribuição \(t-Student\) com \(\nu = n – 1\) graus de liberdade.
O intervalo de confiança para \(\mu\) com nível de confiança de \((1 – \alpha)100,0\%\), é dado pela expressão (9.9).
\[ P\left[\bar{x}-t_{\left(\nu;\frac{\alpha}{2} \right)} \frac{s}{\sqrt{n}} < \mu < \bar{x}+t_{\left(\nu;\frac{\alpha}{2} \right)} \frac{s}{\sqrt{n}} \right]=1 - \alpha. \tag{9.9}\]
O erro máximo da estimativa é dado por: \[ e=t_{\left(v;\frac{\alpha}{2} \right)} \frac{s}{\sqrt{n}} \]
O tamanho da amostra para estimar a média é obtido pela expressão (9.10). \[ n=\left(\frac{t_{\left(v;\frac{\alpha}{2} \right)}s}{e} \right)^2. \tag{9.10}\]
Exemplo 9.15 Seja uma amostra de 20 árvores, de uma espécie de Eucalipto pertencente a um povoamento florestal, em que a variável DAP (diâmetro à altura do peito) apresentou uma média de 18,0 cm e um desvio padrão de 2,5 cm. Construir um intervalo de confiança de 95,0% para a média populacional \(\mu\).
Neste caso, tem-se:
- \(n=20 \Rightarrow v=n-1=20-1=19\) graus de liberdade;
- \(\bar{x}=18,0\) cm;
- \(s=2,5\) cm;
- \((1 - \alpha)=0,95 \Rightarrow \alpha=0,05 \Rightarrow \frac{\alpha}{2}=0,025\).
\[ t_{\left(v;\frac{\alpha}{2} \right)}=t_{\left(19;0,025\right)}=? \]
Consultando a Tabela A 3, tem-se que o valor de \(t\) que deixa uma probabilidade acima dele de 2,5% com 19 graus de liberdade é igual a 2,0930, conforme esquema abaixo:
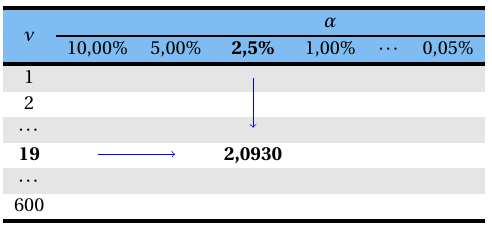
Logo, \[ t_{\left(19;0,025\right)}=2,0930. \]
Através da expressão (9.9), tem-se que: \[ 18,0-2,0930\frac{2,5}{\sqrt{20}} < \mu < 18,0+2,0930\frac{2,5}{\sqrt{20}} \] \[ 18,0 - 1,17 < \mu < 18,0 + 1,17 \]
\[ \Rightarrow IC_{0,95}(\mu):~[16,83~\textrm{cm};~ 19,17~\textrm{cm}]. \]
Esse resultado mostra que é de 95,0% a confiança, do verdadeiro DAP médio das árvores de Eucalipto estar entre 16,83 e 19,17 cm. Do ponto de vista de amostragem isto quer dizer que, se forem retiradas várias amostras aleatórias dentro desta população, calculando-se os valores de \(\bar{\text{x}}\) e \(s\) para cada amostra, e construindo o intervalo de confiança para \(\mu\) em cada amostra, 95,0% dos intervalos conterão em seu interior o verdadeiro valor da média populacional \(\mu\).
9.7.2 Intervalo de Confiança para a Diferença entre duas Médias Independentes
A diferença de médias amostrais, \(\bar{x}_1-\bar{x}_2\), estima a diferença de médias populacionais, \(\mu_1 - \mu_2\), por ponto. A partir do conhecimento das distribuições teóricas \(Z\) e \(t\), pode-se construir um intervalo de confiança de \((1 – \alpha)100,0\%\) para a diferença de médias \(\mu_1 - \mu_2\).
Para a construção do intervalo de confiança para a diferença entre duas médias independentes, tem-se as seguintes situações, descritas a seguir.
9.7.2.1 Grandes Amostras ou Variâncias Populacionais Conhecidas
O intervalo de confiança associado a um determinado nível de confiança, para a diferença entre duas médias, \(\mu_1 - \mu_2\), quando se tem grandes amostras, \(n_1\) e \(n_2 \geq 30\), ou variâncias populacionais, \(\sigma_{1}^2\) e \(\sigma_{2}^2\), conhecidas, é dado pela expressão (9.11).
\[ P\left[(\bar{x}_{1}-\bar{x}_{2})-Z_\frac{\alpha}{2}\sqrt{\frac{\sigma_{1}^2}{n_1}+\frac{\sigma_{2}^2}{n_2}} < (\mu_1 - \mu_2) <\right. \] \[ \left.(\bar{x}_{1}-\bar{x}_{2})+Z_\frac{\alpha}{2}\sqrt{\frac{\sigma_{1}^2}{n_1}+\frac{\sigma_{2}^2}{n_2}}\right]=1 - \alpha. \tag{9.11}\]
Não se conhecendo \(\sigma_{1}^2\) e \(\sigma_{2}^2\) pode-se usar \(s_{1}^2\) e \(s_{2}^2\), desde que \(n_1\) e \(n_2 \geq 30\).
Exemplo 9.16 Sejam:
Se da população de suínos da raça 1 e da raça 2, são retiradas amostras de tamanhos: \(n_1 = 10\) e \(n_2 = 11\), respectivamente, obtendo-se: \(\bar{x}_{1}=110,0\) kg e \(\bar{x}_{2}=107,0\) kg. Construir um intervalo com 95,0% de confiança para a diferença de médias das duas raças.
Tem-se então que:
- \(\sigma_{1}^2=166,0\) Kg\(^2\) e \(\sigma_{2}^2=127,0\) Kg\(^2\);
- \(({\bar{\text{x}}_1-\bar{\text{x}_2}})=110,0 - 107,0 = 3,0\) kg \(\Rightarrow\) estimativa por ponto de \((\mu_1 - \mu_2)\);
- \((1 - \alpha)=0,95 \Rightarrow \alpha=0,05 \Rightarrow \frac{\alpha}{2}=0,025 \Rightarrow Z_{0,025}=1,96\) (Tabela A 1).
Através da expressão (9.11), tem-se que:
\[ 3,0-1,96\sqrt{\frac{166,0}{10}+\frac{127,0}{11}} < (\mu_1 - \mu_2) < \] \[ 3,0+1,96\sqrt{\frac{166,0}{10}+\frac{127,0}{11}} \]
\[ 3,0-10,4 < (\mu_1 - \mu_2) < 3,0+10,4. \]
Logo,
Esse resultado mostra que é de 95,0% a confiança, da verdadeira diferença dos pesos médios entre as duas raças de suínos estar entre -7,4 e 13,4 kg. Como o intervalo de confiança abrange o zero, pode-se concluir que o peso médio da raça 1 não difere do peso médio raça 2. Caso o intervalo de confiança não tivesse abrangido o zero, concluiria-se que as médias difeririam entre si.
9.7.2.2 Pequenas Amostras e Variâncias Populacionais Desconhecidas
O intervalo de confiança associado a um determinado nível de confiança, para a diferença entre duas médias, \(\mu_1 - \mu_2\), quando se tem pequenas amostras, \(n_1 < 30\) e \(n_2 < 30\), e variâncias populacionais, \(\sigma_{1}^2\) e \(\sigma_{2}^2\), desconhecidas, pode ser determinado considerando as seguintes situações:
- Variâncias Populacionais Iguais: Neste caso, para saber se as variâncias populacionais, \(\sigma_{1}^2\) e \(\sigma_{2}^2\), são iguais, deve-se fazer primeiro o Teste F, o qual será visto com detalhes no Capítulo 10.
Dessa forma, um intervalo de confiança de \((1 - \alpha)100,0\%\), para a diferença de médias, \(\mu_1 - \mu_2\), pode ser construído utilizando a distribuição \(t\), e é dado pela expressão (9.12).
\[ P\left[(\bar{x}_1-\bar{x}_2)-t_{\left(v;\frac{\alpha}{2}\right)}\sqrt{s_{p}^2\left(\frac{1}{n_1}+\frac{1}{n_2}\right)} < (\mu_1 - \mu_2) < \right. \] \[ \left.(\bar{x}_1-\bar{x}_2)-t_{\left(v;\frac{\alpha}{2}\right)}\sqrt{s_{p}^2\left(\frac{1}{n_1}+\frac{1}{n_2}\right)} \right]=1 - \alpha, \tag{9.12}\]
em que:
- \(s_{p}^2=\frac{(n_{1}-1)s_{1}^2+(n_{2}-1)s_{2}^2}{n_{1}+n_{2}-2}\) (variância ponderada);
- \(t_{\left(\nu; \frac{\alpha}{2}\right)}\) é o valor tabelado de \(t\), para: \(\nu=n_{1}+n_{2} -2\) graus de liberdade, que deixa uma probabilidade acima dele de \(\frac{\alpha}{2}\).
Exemplo 9.17
Sejam:Se da população de suínos da raça 1 e da raça 2, são retiradas amostras de tamanhos: \(n_1 = 10\) e \(n_2 = 11\), respectivamente, obtendo-se: \(\bar{x}_{1}=112,0\) kg e \(s_{1}^2=156,0\) kg\(^2\); \(\bar{x}_{2}=105,0\) kg e \(s_{2}^2=165,0\) kg\(^2\).
Considerando que, \(\sigma_{1}^2\) e \(\sigma_{2}^2\) são iguais, construir um intervalo de confiança de 95,0% de confiança para a diferença de médias das duas raças.
Tem-se então que:
- \(({\bar{\text{x}}_1-\bar{\text{x}_2}})=112,0 - 105,0 = 7,0\) kg \(\Rightarrow\) estimativa por ponto de \((\mu_1 - \mu_2)\);
- \((1 - \alpha)=0,95 \Rightarrow \alpha=0,05 \Rightarrow \frac{\alpha}{2}=0,025\);
- \(s_{p}^2=\frac{(n_{1}-1)s_{1}^2+(n_{2}-1)s_{2}^2}{n_{1}+n_{2}-2}=\frac{(10-1)156,0+(11-1)165,0}{10+11-2}=160,74\) kg\(^2\);
- \(v=n_{1}+n_{2} -2=10+11-2=19\) graus de liberdade.
Consultando a Tabela A 3, tem-se que o valor de \(t\) que deixa uma probabilidade acima dele de 2,5% com 19 graus de liberdade é igual a 2,0930.
Logo,Através da expressão (9.12), tem-se que:
\[ 7,0-2,0930\sqrt{160,74\left(\frac{1}{10}+\frac{1}{11} \right)} < (\mu_1 - \mu_2) < \] \[ 7,0+2,0930\sqrt{160,74\left(\frac{1}{10}+\frac{1}{11} \right)} \]
\[ 7,0-11,60 < (\mu_1 - \mu_2) < 7,0+11,60. \]
Logo,
Esse resultado mostra que é de 95,0% a confiança, da verdadeira diferença dos pesos médios entre as duas raças de suínos estar entre -4,60 e 18,60 kg. Pode-se concluir que, as duas raças de suínos não diferem entre si com relação ao peso médio, pois o intervalo de confiança abrange o zero.
- Variâncias Populacionais Diferentes:
Neste caso, também deve-se fazer primeiro o Teste F para verificar se as variâncias são diferentes.
O intervalo de confiança de \((1 - \alpha)100,0\%\), para a diferença de médias, \(\mu_1 - \mu_2\), é dado pela expressão 9.13. \[ P\left[(\bar{x}_1-\bar{x}_2)-t_{\left(v;\frac{\alpha}{2}\right)}\sqrt{\left(\frac{s_{1}^2}{n_1}+\frac{s_{2}^2}{n_2}\right)} < (\mu_1 - \mu_2) < \right. \] \[ \left.(\bar{x}_1-\bar{x}_2)-t_{\left(v;\frac{\alpha}{2}\right)}\sqrt{\left(\frac{s_{1}^2}{n_1}+\frac{s_{2}^2}{n_2}\right)} \right]=1 - \alpha, \tag{9.13}\] em que: \(t_{\left(\nu; \frac{\alpha}{2}\right)}\) é o valor tabelado de \(t\) com \(\nu\) graus de liberdade que deixa uma probabilidade acima dele de \(\frac{\alpha}{2}\), sendo “\(\nu\)” dado pela expressão (9.14).
\[ \nu=\frac{\left(\frac{s_{1}^2}{n_1}+\frac{s_{2}^2}{n_2}\right)^2}{\frac{\left(\frac{s_{1}^2}{n_1}\right)^2}{n_{1}-1}+\frac{\left(\frac{s_{2}^2}{n_2}\right)^2}{n_{2}-1}}, \tag{9.14}\] conhecida como Fórmula de Satterthwaite.
Exemplo 9.18 Considerando o Exemplo 9.17, e supondo que \(\sigma_{1}^2\) e \(\sigma_{2}^2\) sejam estatisticamente diferentes, construir um intervalo de confiança de 95,0% de confiança para a diferença de médias das duas raças.
Assim, tem-se que:
- \(({\bar{\text{x}}_1-\bar{\text{x}_2}})=112,0 - 105,0 = 7,0\) kg \(\Rightarrow\) estimativa por ponto de \((\mu_1 - \mu_2)\);
- \((1 - \alpha)=0,95 \Rightarrow \alpha=0,05 \Rightarrow \frac{\alpha}{2}=0,025\);
- \(\nu=\frac{\left(\frac{156,0}{10}+\frac{165,0}{11}\right)^2}{\frac{\left(\frac{156,0}{10}\right)^2}{10-1}+\frac{\left(\frac{165,0}{11}\right)^2}{11-1}}=19\) graus de liberdade.
Através de (9.13), tem-se que:
\[ 7,0-2,0930\sqrt{\left(\frac{156,0}{10}+\frac{165,0}{11} \right)} < (\mu_1 - \mu_2) < \] \[ 7,0+2,0930\sqrt{\left(\frac{156,0}{10}+\frac{165,0}{11} \right)} \]
Logo,
Esse resultado mostra que é de 95,0% a confiança, da verdadeira diferença dos pesos médios entre as duas raças de suínos estar entre -4,58 e 18,58 kg. Pode-se concluir que, as duas raças de suínos não diferem entre si com relação ao peso médio, pois o intervalo de confiança abrange o zero. Considere a Tabela 9.1.
9.7.3 Intervalo de Confiança para a Média em Amostras Dependentes
A análise em amostras dependentes é apropriada quando a variável é medida antes e depois, por exemplo, peso de suínos antes e depois de serem submetidos a uma dieta com uma ração especial.

Em que \(d_i\) é o desvio.
O desvio médio é dado por (9.15).
\[ \bar{d}=\frac{\sum_{i=1}^{n}d_{i}}{n}=\bar{y}-\bar{x}. \tag{9.15}\]
O intervalo de confiança de \((1 - \alpha)100,0\%\) para \(\mu_d\), é dado por (9.16). \[ \begin{align} P\left[{\bar{d}}-t_{\left(v;\frac{\alpha}{2}\right)}\frac{s_d}{\sqrt{n}} < \mu_d < {\bar{d}}+t_{\left(v;\frac{\alpha}{2}\right)}\frac{s_d}{\sqrt{n}} \right]=1 - \alpha, \end{align} \tag{9.16}\] em que:
- \(t_{\left(\nu; \frac{\alpha}{2}\right)}\) é o valor tabelado de \(t\) com \(\nu=n-1\) graus de liberdade que deixa uma probabilidade acima dele de \(\frac{\alpha}{2}\);
- \(\mu_{d}=\mu_{x}-\mu_{y}\);
- \(s_{d}=\sqrt{\frac{\sum_{i=1}^{n}d_{i}^{2}-\frac{\left(\sum_{i=1}^{n}d_i\right)^2}{n}}{n-1}}\).
Exemplo 9.19 Um lote de 32 novilhos da raça nelore de 2,5 anos, foram submetidos a um confinamento por 84 dias com cana-de-açúcar e concentrado. Os pesos, em kg, antes e depois do confinamento estão apresentados na Tabela 9.2.
| Animal | Antes (X) | Depois (Y) | d=Ganho de peso (Y - X) |
|---|---|---|---|
| 1 | 332,0 | 422,0 | 90,0 |
| 2 | 333,0 | 423,0 | 90,0 |
| 3 | 338,0 | 424,0 | 86,0 |
| 4 | 337,0 | 422,0 | 85,0 |
| 5 | 332,0 | 424,0 | 92,0 |
| 6 | 340,0 | 427,0 | 87,0 |
| 7 | 340,0 | 422,0 | 82,0 |
| 8 | 335,0 | 423,0 | 88,0 |
| 9 | 340,0 | 431,0 | 91,0 |
| 10 | 335,0 | 422,0 | 87,0 |
| 11 | 339,0 | 429,0 | 90,0 |
| 12 | 336,0 | 428,0 | 92,0 |
| 13 | 340,0 | 424,0 | 84,0 |
| 14 | 336,0 | 431,0 | 95,0 |
| 15 | 337,0 | 429,0 | 92,0 |
| 16 | 331,0 | 428,0 | 97,0 |
| 17 | 331,0 | 428,0 | 97,0 |
| 18 | 337,0 | 424,0 | 87,0 |
| 19 | 330,0 | 422,0 | 92,0 |
| 20 | 339,0 | 430,0 | 91,0 |
| 21 | 336,0 | 423,0 | 87,0 |
| 22 | 337,0 | 427,0 | 90,0 |
| 23 | 336,0 | 426,0 | 90,0 |
| 24 | 332,0 | 430,0 | 98,0 |
| 25 | 332,0 | 431,0 | 99,0 |
| 26 | 337,0 | 430,0 | 93,0 |
| 27 | 332,0 | 422,0 | 90,0 |
| 28 | 333,0 | 423,0 | 90,0 |
| 29 | 336,0 | 429,0 | 93,0 |
| 30 | 340,0 | 427,0 | 87,0 |
| 31 | 340,0 | 432,0 | 92,0 |
| 32 | 339,0 | 424,0 | 85,0 |
Construir um intervalo de confiança de 95,0% de confiamça para a média de ganho de peso \((\mu_d)\) dos novilhos.
Assim, tem-se que:
- \((1 - \alpha)=0,95 \Rightarrow \alpha=0,05 \Rightarrow \frac{\alpha}{2}=0,025\).
- \(v=n-1=32-1=31\) graus de liberdade.
Consultando a Tabela A 3, o valor de \(t\) que deixa uma probabilidade acima dele de 2,5% com 31 graus de liberdade é igual a 2,0395.
Logo,Esse resultado mostra que é de 95,0% a confiança, da verdadeira média do ganho de pesos dos novilhos estar entre 88,8031 e 91,7595 kg. Pode-se concluir que, o confinamento foi eficiente para o ganho de pesos dos novilhos, pois o intervalo de confiança não abrange o zero.
9.7.4 Intervalo de Confiança para a Variância e Desvio Padrão
A variância amostral \(s^2\) é um estimador pontual da variância populacional \(\sigma^2\). Pode-se construir um intervalo de confiança de \((1 – \alpha )100,0\%\) para \(\sigma^2\), utilizando-se a distribuição da variável aleatória \(\chi^2\).
Foi visto no Capítulo 8 que a variável:segue uma distribuição \(\chi^2\) com \(\nu = n – 1\) graus de liberdade.
Na distribuição de \(\chi^2\) pode-se esquematizar uma probablidade de \((1 – \alpha)\), conforme a Figura 9.3.
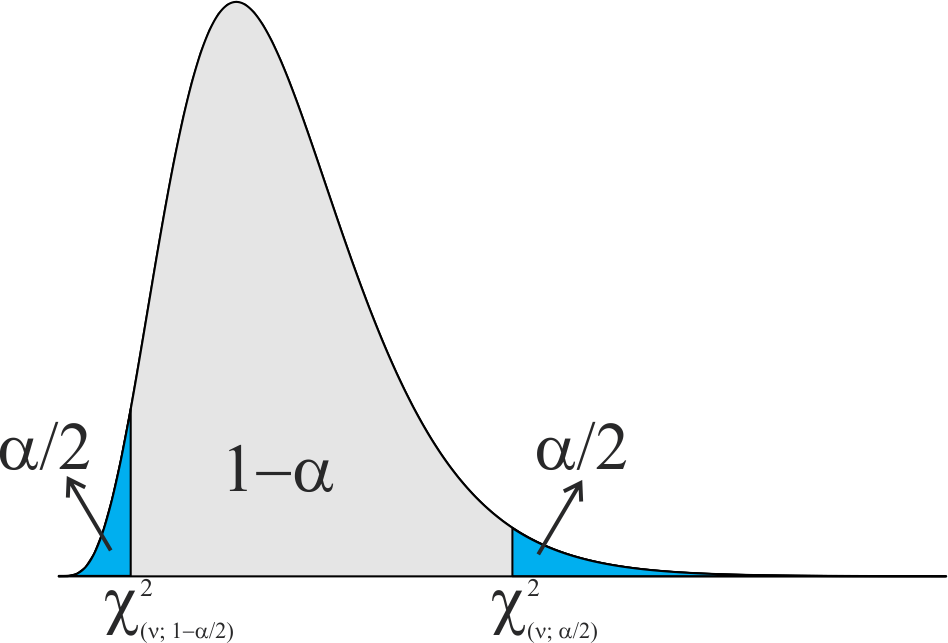
Logo, um intervalo de confiança para \(\sigma^2\), com nível de confiança de \((1 - \alpha)100,0\%\), é dado por (9.17). \[ \begin{align} P\left[\frac{(n-1)s^2}{\chi^{2}_{\left(v;\frac{\alpha}{2} \right) }} < \sigma^2 < \frac{(n-1)s^2}{\chi^{2}_{\left(v;1-\frac{\alpha}{2} \right) }} \right]=1 - \alpha, \end{align} \tag{9.17}\] em que: \(\chi^{2}_{\left(v;\frac{\alpha}{2} \right)}\) e \(\chi^{2}_{\left(v;1-\frac{\alpha}{2} \right)}\) são obtidos na tabela de \(\chi^2\) (Tabelas 4 e 5) para \(v = n – 1\) graus de liberdade.
Exemplo 9.20 Seja uma amostra de 20 árvores, de uma espécie de Eucalipto pertencente a um povoamento florestal, em que a variável DAP (diâmetro à altura do peito) apresentou uma média de 18,0 cm e uma variância de 6,25 cm\(^2\). Construir um intervalo de confiança de 95,0% para a variância populacional \(\sigma^2\). Assim, tem-se que:
- \(s^2=6,25\) cm\(^2\);
- \((1 - \alpha)=0,95 \Rightarrow \alpha=0,05 \Rightarrow \frac{\alpha}{2}=0,025 \Rightarrow 1-\frac{\alpha}{2}=0,975\);
- \(n=20 \Rightarrow v=n-1=20-1=19\) graus de liberdade;
- \(\chi^{2}_{\left(v;\frac{\alpha}{2} \right)}=\chi_{(19;0,025)}^{2}=?\)
- \(\chi^{2}_{\left(v;1-\frac{\alpha}{2} \right) }=\chi_{(19;0,975)}^{2}=?\)
Consultando as Tabelas 4 e 5, tem-se que o valor de \(\chi^2\) que deixa uma probabilidade acima dele de 2,5%, com 19 graus de liberdade é igual a 32,8523. Com 19 graus de liberdade o valor de \(\chi^2\) que deixa uma probabilidade acima dele de 97,5% é igual a 8,9065.
Logo,Esse resultado mostra que é de 95,0% a confiança, do verdadeiro valor da variância do DAP das árvores do povoamento estar entre 3,62 e 14,47 cm\(^2\).
O intervalo de confiança de \((1 – \alpha)100,0\%\) para o desvio padrão populacional \(\sigma\), é dado pela raiz quadrada positiva do intervalo de confiança da variância, dado pela expressão (9.18). \[ \begin{align}\label{eq:icdp} P\left[\sqrt{\frac{(n-1)s^2}{\chi^{2}_{\left(v;\frac{\alpha}{2} \right)}}} < \sigma < \sqrt{\frac{(n-1)s^2}{\chi^{2}_{\left(v;1-\frac{\alpha}{2} \right)}}} \right]=1 - \alpha. \end{align} \tag{9.18}\]
Exemplo 9.21 Considerando o Exemplo 9.20, e utilizando a expressão (9.18), tem-se que o intervalo de confiança 95,0% para o desvio padrão populacional \(\sigma\), é dado por:
Esse resultado mostra que é de 95,0% a confiança, do verdadeiro valor do desvio padrão do DAP das árvores do povoamento estar entre 1,90 e 3,80 cm.
9.7.5 Intervalo de Confiança para Proporções
A proporção amostral \(\hat{p}\) é uma estimativa pontual da proporção populacional \(p\). Pode-se construir um intervalo de confiança de \((1 – \alpha)100,0\%\) para \(p\) utilizando-se a distribuição Z, dado por (9.19). \[ \begin{align} P\left[\hat{p}-Z_{\frac{\alpha}{2}}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} < p < \hat{p}+Z_{\frac{\alpha}{2}}\sqrt{\frac{\hat{p}(1-\hat{p})}{n}} \right]=1 - \alpha. \end{align} \tag{9.19}\]
O erro máximo da estimativa é dado por:O tamanho da amostra dimensionado estatisticamente para estimar proporções, é dado por (9.20). \[ \begin{align} n=\left(\frac{Z_{\frac{\alpha}{2}}}{e}\right)^{2}\hat{p}(1-\hat{p}). \end{align} \tag{9.20}\]
Exemplo 9.22 Foi extraída uma amostra aleatória de 240 laranjeiras de um grande pomar, onde constatou-se que 53 delas estavam atacadas pelo cancro cítrico. Construir um intervalo de confiança de 95,0% para a proporção de plantas doente.
Assim, tem-se que:
- \(n=240\);
- \(x=53\);
- \(\hat{p}=\frac{x}{n}=\frac{53}{240}=0,221=22,10\% \Rightarrow\) Estimativa por ponto de \(p\);
- \((1 - \alpha)=0,95 \Rightarrow \alpha=0,05 \Rightarrow \frac{\alpha}{2}=0,025 \Rightarrow Z_{0,025}=1,96\).
Esse resultado mostra que é de 95,0% a confiança, da verdadeira proporção de plantas atacadas pelo Cancro Cítrico estar entre 0,169 e 0,273.
Pode-se estar interessado também em saber quantas plantas deverão ser investigadas num próximo estudo, para estimar a proporção de plantas doentes com um erro de 4,0% e uma confiança de 95,0%.
Através da expressão (9.20), tem-se que:Portanto, serão necessárias 414 plantas para serem amostradas num próximo estudo, para estimar a proporção de plantas doentes com um erro de 4,0% e uma confiança de 95,0%.
9.7.6 Intervalo de Confiança para a Diferença entre duas Proporções
Frequentemente tem-se o interesse em estimar a diferença entre as proporções de duas populações estudadas.
O intervalo de confiança de \((1\) \(–\) \(\alpha)100,0\%\) para a diferença entre duas proporções, pode ser construído utilizando-se a distribuição Z, dado por (9.21). \[ \begin{align} P&\left[(\hat{p_1}-\hat{p_2})-Z_{\frac{\alpha}{2}}\sqrt{\frac{\hat{p_1}(1-\hat{p_1})}{n_1}+\frac{\hat{p_2}(1-\hat{p_2})}{n_2}} < p_{1} - p_{2} < \right. \nonumber\\ & \quad \left. (\hat{p_1}-\hat{p_2})+Z_{\frac{\alpha}{2}}\sqrt{\frac{\hat{p_1}(1-\hat{p_1})}{n_1}+\frac{\hat{p_2}(1-\hat{p_2})}{n_2}}\right]=1 - \alpha. \end{align} \tag{9.21}\]
Exemplo 9.23 Foram extraídas duas amostras aleatórias de laranjeiras de um gran-de pomar, que apresentavam incidências do cancro cítrico. A amostra 1, composta de 200 laranjeiras, foi proveniente de uma parcela que não recebeu o tratamento fitossanitário, chamada de controle. A amostra 2, composta de 150 laranjeiras, foi proveniente de uma parcela em que as plantas foram submetidas a um tratamento fitossanitário para o controle do cancro cítrico. Na amostra 1, constatou-se que 52 laranjeiras estavam atacadas pelo cancro cítrico. Constatou-se pela análise da amostra 2 que, 18 laranjeiras estavam atacadas pelo cancro cítrico.
Construir um intervalo de confiança de 95,0% para a diferença entre as proporções das duas amostras. Com base nos resultados pode-se afirmar que as proporções são diferentes?
Para a construção do intervalo de confiança, tem-se que: \[\begin{align*} \textrm{Amostra~ 1}\begin{cases} n_1=200; \\ x_{1}=52; \\ \hat{p_1}=\frac{52}{200}=0,26=26,0\%. \end{cases} \end{align*}\]
\[\begin{align*} \textrm{Amostra}~ 2\begin{cases} n_1=150; \\ x_{1}=18; \\ \hat{p_1}=\frac{18}{150}=0,12=12,0\%. \end{cases} \end{align*}\]
Tem-se então que:é a estimativa por ponto de \(p_{1}-p_{2}\).
Assim, tem-se que:Esse resultado mostra que é de 95,0% a confiança, da verdadeira diferença entre as proporções das duas amostras estar entre 0,06 e 0,22. Com base nos resultados pode-se afirmar que as proporções são diferentes, pois o intervalo de confiança não abrange o zero.
Exercícios propostos
Exercício 9.1 Numa lavoura de milho foi tomada uma amostra de 40 plantas, anotando-se as alturas, em cm. Os resultados forneceram:
- Encontre as estimativas por ponto de \(\mu\) e \(\sigma\);
- Construa um intervalo de confiança de 95,0% para a média \(\mu\) e interprete;
- Construa um intervalo de confiança de 99,0% para a média \(\mu\) e interprete;
- Confronte os resultados de (b) e de (c) e discuta as diferenças;
- Quantos plantas você recomenda usar num próximo estudo, para estimar a média \(\mu\) com 95,0% de confiança e um erro:
- 10,0% menor que em (b);
- de 3,0 cm.
Exercício 9.2 Foi tomado ao acaso um lote de 15 bovinos no rebanho de um criador, fornecendo média de 240,0 kg e desvio padrão de 15,0 kg.
- Construa um intervalo de confiança de 95,0% para o peso médio do rebanho;
- Construa um intervalo de confiança de 90,0% para o desvio padrão do peso do rebanho;
- Quantos animais você recomenda usar num próximo estudo, para estimar a média com um erro 10,0% menor que em (a), e 95,0% de confiança.
Exercício 9.3 Estão sendo estudados 2 processos para conservar alimentos quanto ao tempo de duração (X), em dias. No processo A: X \(\sim N(\mu_{A}; 100,0)\); e no processo B: X \(\sim N(\mu_{B}; 125,0)\). Foram Sorteadas duas amostras independentes, a de A com 16 latas apresentou um tempo médio de duração igual a 50,0 dias, e a de B com 25 latas apresentou um tempo médio de duração igual a 60,0 dias.
- Construa um intervalo de confiança de 95,0% para \(\mu_A\) e \(\mu_B\). Interprete os resultados;
- Construa um intervalo de confiança de 95,0% para \(\mu_A-\mu_B\). Interprete os resultados. Com base nos resultados você acha que existe diferença significativa entre as médias de conservação dos dois processos? Justifique.
Exercício 9.4 Num estudo com duas espécies de eucalipto, sortearam-se duas parcelas em plantações com idade de 6 anos, anotando-se os seus rendimentos de madeira, em m\(^3\). Os resultados foram os seguintes:
| Espécie | n | Média | Desvio padrão |
|---|---|---|---|
| E. grandis | 28 | 0,43 | 0,06 |
| E. saligna | 24 | 0,39 | 0,07 |
- Construa os intervalos de confiança de 95,0% para as médias \(\mu_g\) e \(\mu_s\). Com base nestes resultados você afirmaria que E. grandis é superior a E. saligna, para a produtividade de madeira aos seis anos? Justifique;
- Construa o intervalo de 95,0% de confiança para a diferença entre as médias das duas espécies \(\mu_g-\mu_s\). Admita que: \(\sigma_{g}^{2}=\sigma_{s}^{2}\). Com base nesse intervalo conclua sobre a diferença de rendimentos das duas espécies;
- Refaça o item (b) considerando que: \(\sigma_{g}^{2}\neq\sigma_{s}^{2}\).
Exercício 9.5 Num estudo com animais das raças Guzerá e Nelore, os animais foram submetidos a um confinamento tratando-se todos os animais com uma mesma ração. Após o período experimental anotou-se o ganho de peso dos animais, em kg. Os resultados foram os seguintes:
| Raça | n | Média | Desvio padrão |
|---|---|---|---|
| Guzerá | 28 | 81,0 | 5,6 |
| Nelore | 25 | 79,0 | 7,1 |
- Construa um intervalo de confiança de 95,0% para as médias das duas raças;
- Construa um intervalo de confiança de 95,0% para os desvios padrão das duas raças;
- Construa um intervalo de confiança de 95,0% para a diferença entre o ganho médio de peso das duas raças. Assuma que as variâncias populacionais são iguais;
- Construa um intervalo de confiança de 95,0% para a diferença entre o ganho médio de peso das duas raças. Assuma que as variâncias populacionais são diferentes;
- Pelos resultados você arriscaria afirmar que o peso médio da raça Guzerá é superior ao da raça Nelore? Justifique.
Exercício 9.6 Uma empresa florestal fornece escoramentos de eucalipto para a construção civil. Para tomar uma decisão sobre o momento de cortar um determinado talhão no reflorestamento, o Engenheiro Florestal responsável realiza uma amostragem aleatória no talhão, obtendo-se os seguintes resultados, em cm.
| 14,6 | 15,8 | 11,2 | 12,5 | 12,6 | 13,4 | 17,6 | 16,7 | 18,5 | 15,1 |
| 15,2 | 14,1 | 13,2 | 14,1 | 15,0 | 15,6 | 16,7 | 16,1 | 17,0 | 11,8 |
| 19,0 | 10,6 | 13,3 | 14,2 | 16,8 | 15,3 | 15,3 | 14,2 | 16,3 | 17,5 |
Com base nesta amostra construa um intervalo de confiança de 95,0% para o diâmetro médio desse talhão. Interprete.
Exercício 9.7 Retirou-se uma amostra de 40 tubérculos de batata, e observou-se uma média de produção de 201,0 g e uma variância de 152,7635 g\(^2\). Construa um intervalo de confiança de 95,0% para a variância e para o desvio padrão populacional.
Exercício 9.8 Foi feito um levantamento na região sul de Minas por meio de uma amostra aleatória, anotando-se as propriedades rurais onde o pecuarista faz a vacinação para controlar a raiva bovina. Os dados obtidos mostraram que em 213 propriedades visitadas, 129 vacinaram o rebanho para prevenção da raiva nos dois últimos anos.
- Estime a proporção por ponto dos produtores da região que vacinam seus rebanhos contra a raiva;
- Construa um intervalo de confiança de 95,0% para a proporção \(p\);
- Qual é o erro da estimativa para estimar \(p\) com 99,0% de confiança;
- Quantas propriedades deverão ser visitadas para estimar \(p\) com um erro de 3,0% e uma confiança de 95,0%.
Exercício 9.9 Foram semeadas sementes de uma espécie de orquídeas em dois substratos (A e B) diferentes. No substrato A foram semeadas 80 sementes, e verificou-se que 65 sementes germinaram. No substrato B foram semeadas 75 sementes, e verificou-se que 56 sementes germinaram. Construir um intervalo de confiança de 95,0% para a diferença entre as proporções dos dois substratos. Com base nos resultados pode-se afirmar que os substratos são diferentes?