10 Teoria da Decisão – Estatística Básica aplicada às Ciências Agrárias

10.1 Introdução

No Capítulo 9, o objetivo era encontrar uma estimativa para um parâmetro populacional desconhecido, sendo que tal estimativa permitia fazer uma afirmação sobre o parâmetro, considerando um determinado nível de confiança. Porém, com frequência, temos ideia ou somos informados sobre um possível valor do parâmetro, e para darmos continuidade ao nosso estudo, somos obrigados a aceitar ou rejeitar tal valor. Com base em informações obtidas numa amostra aleatória, é estatisticamente possível, tomar uma decisão quanto à aceitação ou rejeição da afirmação feita sobre um parâmetro populacional desconhecido.

10.2 Teste de Hipóteses

Um teste de hipóteses é uma regra de decisão que, permite aceitar ou rejeitar uma hipótese formulada sobre um determinado parâmetro populacional, baseando-se em informações contidas numa amostra aleatória.

10.2.1 Hipóteses Estatísticas

Uma afirmação feita sobre um parâmetro populacional em estudo é chamada de hipótese estatística. A hipótese estatística divide-se em duas partes complementares.

Hipótese de Nulidade: É a hipótese que será testada, ou seja, admite ausência de diferenças entre os parâmetros testados, e em notação usa-se $H_0$.

Exemplo 10.1 Considere um teste sobre a média populacional $\mu$, do qual se pode formular as seguintes hipóteses de nulidade:

$H_{0}: \mu=\mu_0$, ou
$H_{0}: \mu \geq \mu_0$, ou
$H_{0}: \mu \leq \mu_0$.

Hipótese Alternativa: É a hipótese que afirma o contrário de $H_0$. É qualquer hipótese diferente de $H_0$, isto é, aquela que será aceita caso o teste indique que $H_0$ deva ser rejeitada, e em notação denota-se por $H_a$.

Exemplo 10.2 De acordo com o Exemplo 10.1, pode-se formular as respectivas hipóteses alternativas:

$H_{a}: \mu \neq \mu_0$, ou
$H_{a}: \mu < \mu_0$, ou
$H_{a}: \mu > \mu_0$.

Vale ressaltar algumas observações:

Estabelecer $H_0$ e $H_a$ depende exclusivamente da natureza do problema em estudo;
Por convenção os símbolos: =, $\geq$ e $\leq$ estão associados com $H_0$, e os símbolos: $\neq$, < e > com $H_a$.
A rejeição de $H_0$ implicará na aceitação de $H_a$, e vice-versa, isto é, $H_0$ e $H_a$ são complementares.

10.3 Erros Cometidos ao se Realizar um Teste de Hipóteses

Como a tomada de decisões sobre a aceitação ou rejeição de uma hipótese, está baseada apenas em informações contidas em dados amostrais, dois tipos de erros podem ser cometidos, a saber:

Erro Tipo I: É o erro que se comete ao rejeitar $H_0$ quando ela é verdadeira. A probabilidade de se cometer esse erro é representada por $\alpha$, e define o nível de significância do teste.
Erro Tipo II: É o erro que se comete ao aceitar $H_0$ quando ela é falsa. A probabilidade de se cometer esse erro é representada por $\beta$. Ao passo que, $1-\beta$ representa a probabilidade de rejeitar uma hipótese incorreta, denominada de poder do teste.

A Tabela 10.1 resume a natureza dos erros envolvidos no processo de decisão através dos testes de hipóteses.

Tabela 10.1: Erros envolvidos na realização de um teste de hipóteses

DECISÃO \ REALIDADE	$H_0$ verdadeira	$H_0$ falsa
Aceitar $H_0$	Decisão correta $(1-\alpha)$	Erro Tipo II $(\beta)$
Rejeitar $H_0$	Erro Tipo I $(\alpha)$	Decisão Correta $(1-\beta)$

Para que um teste de hipóteses seja considerado bom, deve-se ter uma pequena probabilidade de rejeitar $H_0$ se esta for verdadeira, mas também uma grande probabilidade de rejeitá-la se ela for falsa.

Vale ressaltar que os erros tipo I e II são inversamente correlacionados, isto é, o aumento da probabilidade de ocorrência de um reduz a probabilidade de ocorrência do outro. Desse modo, a única forma de diminuir as probabilidades $\alpha$ e $\beta$ simultaneamente, é aumentando o tamanho da amostra.

Neste capítulo serão realizados testes de hipóteses em que apenas o Erro Tipo I é controlado, chamados Testes de Significância, em que o nível de significância $\alpha$ é fixado.

10.4 Significância de um Teste de Hipóteses

Um teste de hipóteses é significativo a um nível $\alpha$ de probabilidade, se a hipótese $H_0$ for rejeitada a esse nível, caso contrário o teste é não significativo a esse nível. Significativo a um nível $\alpha$ indica que, é inferior a $\alpha$ a probabilidade das diferenças detectadas terem sido casuais.

A escolha de $\alpha$ é arbitrária, dependendo dos objetivos do trabalho. Em geral, usa-se fixar $\alpha$ em 5,0% ou 1,0%. Em função do valor de $\alpha$, as tabelas das distribuições teóricas de probabilidades fornecem os valores críticos para os testes.

10.5 Teste Unilateral e Bilateral

De acordo com o objetivo do teste, pode-se usar os dois extremos da distribuição teórica de probabilidade para a região crítica, chamado de Teste Bilateral , ou então apenas um dos extremos da distribuição, chamado de Teste Unilateral.

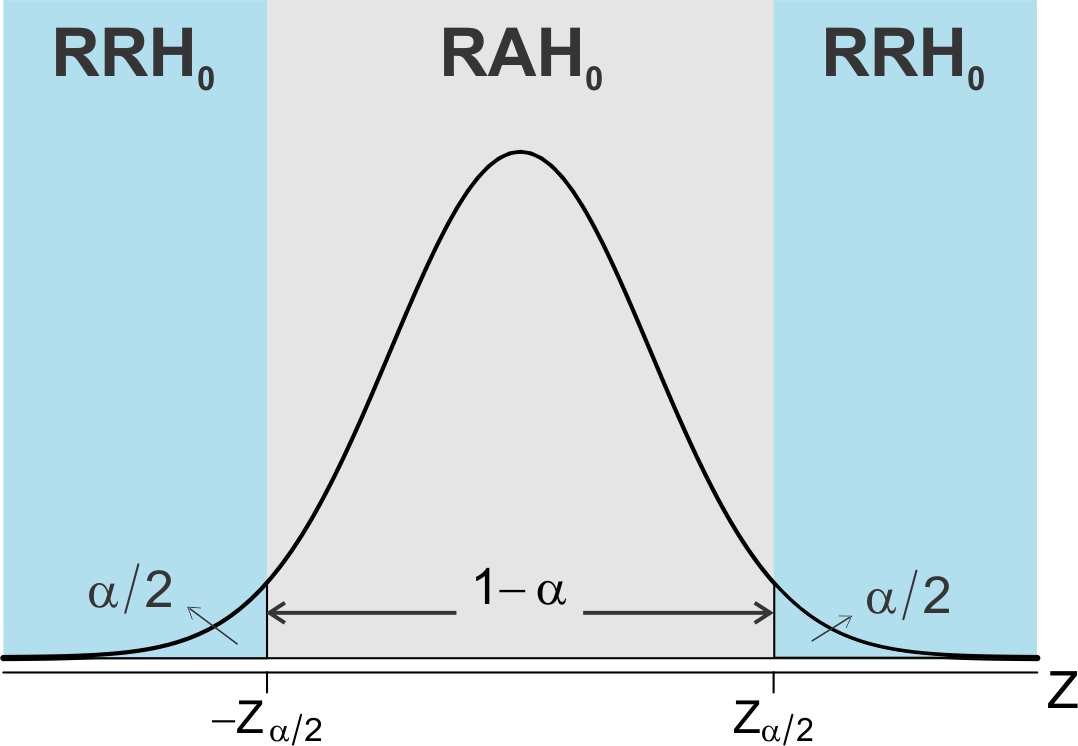
Teste Bilateral: A região de rejeição da hipótese $H_0$ $(RRH_0)$, fica estabelecida nos dois extremos da curva correspondente à distribuição teórica de probabilidades utilizada.

Exemplo 10.3 Seja um teste para a média $\mu$ de uma distribuição normal. Pode-se então formular as seguintes hipóteses:

\[\begin{align*} \begin{cases} H_{0}:\mu=\mu_0;\\ H_{a}: \mu \neq \mu_0. \end{cases} \end{align*}\]

Neste caso, a hipótese $H_{a}$ especifica que $\mu$ pode ser tanto maior quanto menor que $\mu_0$. A representação gráfica deste teste está apresentada na Figura 10.1.

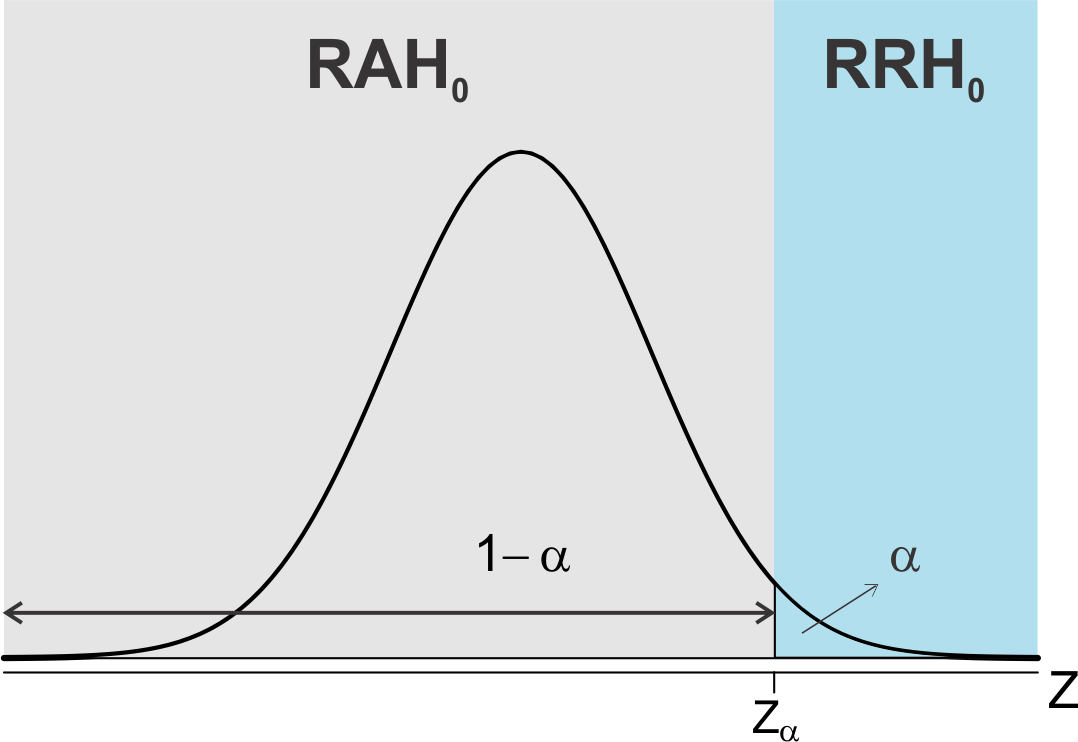
Figura 10.1: Representação gráfica das regiões de um teste de hipótese bilateral.

Teste Unilateral à direita: A região de rejeição da hipótese $H_{0}$, fica estabelecida no lado direito da curva correspondente à distribuição teórica de probabilidades utilizada.

Exemplo 10.4 Considerando o exemplo anterior pode-se formular a seguintes hipóteses:

\[\begin{align*} \begin{cases} H_{0}:\mu=\mu_0 ~ou~ \mu \leq \mu_0;\\ H_{a}: \mu > \mu_0. \end{cases} \end{align*}\]

Cuja representação gráfica está apresentada na Figura 10.2.

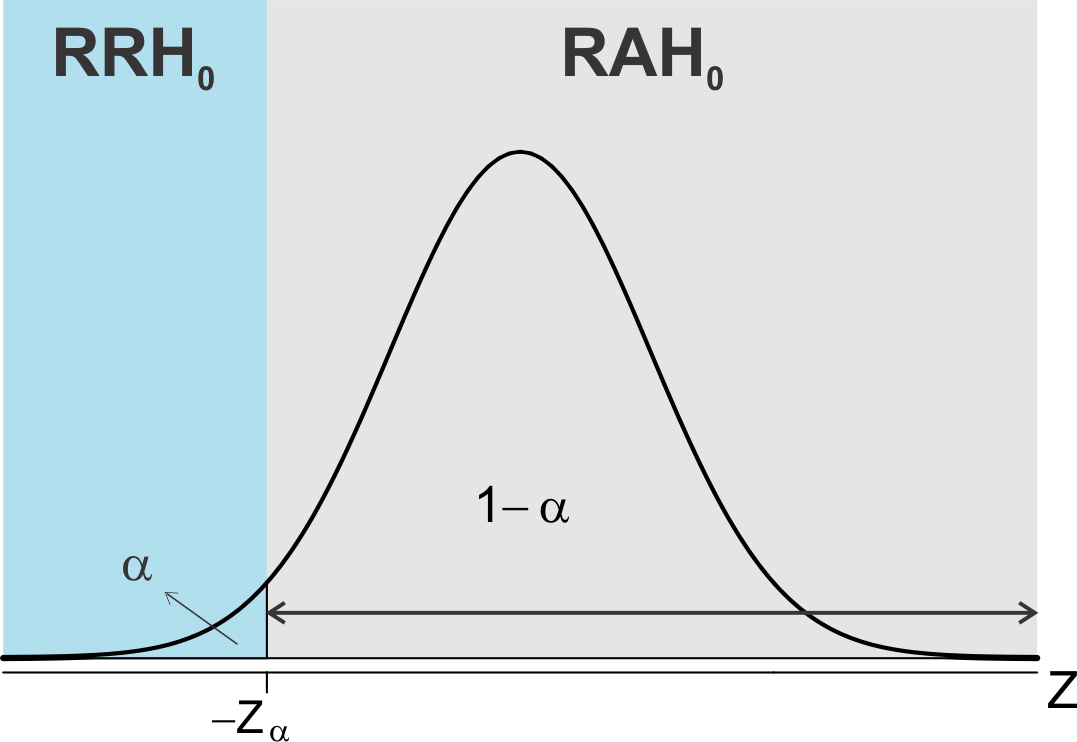
Figura 10.2: Representação gráfica das regiões de um teste de hipótese unilateral à direita.

Teste Unilateral à esquerda: A região de rejeição da hipótese $H_{0}$, fica estabelecida no lado esquerdo da curva correspondente à distribuição teórica de probabilidades utilizada.

Exemplo 10.5 Para o exemplo anterior pode-se formular a seguintes hipóteses:

\[\begin{align*} \begin{cases} H_{0}:\mu=\mu_0 ~ou~ \mu \geq \mu_0;\\ H_{a}: \mu < \mu_0. \end{cases} \end{align*}\]

Cuja representação gráfica está apresentada na Figura Figura 10.3.

Figura 10.3: Representação gráfica das regiões de um teste de hipótese unilateral à esquerda.

10.6 Passos para Execução de um Teste de Hipóteses

Um teste de hipóteses sempre se refere a uma hipótese de nulidade. Para se decidir se as diferenças entre os parâmetros da população são ou não estatisticamente significativos, deve-se submeter os dados amostrais a um teste de hipóteses. Para realização de um teste de hipóteses os seguintes passos devem ser seguidos:

Formular as hipóteses $H_{0}$ e $H_{a}$, segundo a natureza do problema em estudo;
Especificar o nível de significância do teste, ou seja, o valor de $\alpha$;
Escolher o teste apropriado, estabelecendo a região crítica $(RRH_0)$ na distribuição teórica de probabilidades;
Calcular o valor do teste através dos dados amostrais;
Decisão (Conclusão). Comparar o valor calculado do teste com o valor crítico (tabelado). Se o valor calculado do teste pertencer a região de aceitação de $H_{0}$ $(RAH_{0})$, aceita-se $H_{0}$, caso contrário, rejeita-se $H_{0}$, com nível de significância $\alpha$.

Nas próximas seções, serão utilizados as distribuições de probabilidades e resultados, vistos no Capítulo 8, para a construção de testes de hipóteses para parâmetros populacionais de interesse.

10.7 Teste para a Média de uma Distribuição Normal

Para o teste da média de uma distribuição normal, tem-se as seguintes situações, dadas a seguir.

10.7.1 Grandes Amostras ou Variância Populacional Conhecida

Quando se tem grandes amostras $(n \geq 30)$, ou se conhece a variância populacional $\sigma^2$, o procedimento do teste é dado da seguinte forma:

Formular as hipóteses: $H_0$ e $H_a$. Teste Bilateral: \[\begin{align*} \begin{cases} H_{0}: \mu=\mu_0;\\ H_{a}: \mu \neq \mu_0. \end{cases} \end{align*}\]

Teste Unilateral à Direita: \[\begin{align*} \begin{cases} H_{0}: \mu=\mu_0;\\ H_{a}: \mu > \mu_0. \end{cases} \end{align*}\] Teste Unilateral à Esquerda: \[\begin{align*} \begin{cases} H_{0}: \mu=\mu_0;\\ H_{a}: \mu < \mu_0. \end{cases} \end{align*}\]

Especificar do nível de significância do teste, ou seja, o valor de $\alpha$;
Escolha do teste apropriado, estabelecendo a região crítica ($RRH_0$) na distribuição teórica de probabilidades. Neste caso, o teste apropriado é o Teste Z, cuja estatística do teste é dada por (10.1). \[ \begin{align} Z & = \frac{\bar{x}-\mu}{\frac{\sigma}{\sqrt{n}}}, \end{align} \tag{10.1}\] em que $Z \sim N(0,0; 1,0)$;
Cálculo da estatística do teste através dos dados amostrais, denotado por $Z_c$, dado por (10.2). \[ \begin{align} Z_c & = \frac{\bar{x}-\mu_0}{\frac{\sigma}{\sqrt{n}}}, \end{align} \tag{10.2}\] em que $\mu_0$ é o valor de $\mu$ sob $H_0$.

Em seguida, compara-se o valor de $Z_c$ com o valor crítico ($Z_{tab}$), consultando a Tabela de Z (Tabela A 1 ou Tabela A 2).

Decisão:
- Se $|Z_c| > |Z_{tab} = Z_{\alpha}$ (unilateral) ou $Z_{\alpha/2}$ (bilateral)$|$, então rejeita-se $H_0$. De outra forma, se $Z_c \in RRH_0$, então rejeita-se $H_0$;
- Se $|Z_c| \leq |Z_{tab} = Z_{\alpha}$ (unilateral) ou $Z_{\alpha/2}$ (bilateral)$|$ , então aceita-se $H_0$. De outra forma, se $Z_c \in RAH_0$, então aceita-se $H_0$.

Exemplo 10.6 Técnicos do INMETRO desejam avaliar um processo para conservar alimentos enlatados, cuja principal variável de interesse é o tempo de duração dos mesmos, que obedece a uma distribuição normal com variância igual a 100 dias$^2$. A indústria que utiliza o processo afirma que o tempo médio de duração é de 70 dias. Os técnicos retiraram uma amostra de 25 latas e a média encontrada foi de 60 dias. Ao nível de 1,0%, pode-se aceitar ou não a afirmação da indústria.

Neste caso embora o tamanho da amostra é menor do que 30, a variância populacional é conhecida, sendo igual a 100 dias$^2$, e assim seguindo os passos descritos anteriormente, tem-se:

Formular as hipóteses: $H_{0}$ e $H_{a}$.

Neste caso, os dados do exemplo sugerem um teste unilateral à esquerda. Logo, tem-se as hipóteses: \[\begin{align*} \begin{cases} H_{0}:\mu=70;\\ H_{a}: \mu < 70. \end{cases} \end{align*}\]

Especificar o nível de significância $\alpha$: $\alpha=0,01~\textrm{ou}~1,0\%$.
Escolha do teste apropriado, estabelecendo a região crítica ($RRH_0$) na distribuição teórica de probabilidades.

Neste caso, o teste apropriado é o Teste Z dado por (10.1).

Consultando a Tabela A 2, tem-se que o valor de Z que deixa uma probabilidade acima dele de $0,01$ é igual a $2,33$. Consulta-se dentro do corpo da tabela o valor referente a $0,01$ ou mais próximo, neste caso o $0,0099$, conforme esquema abaixo:

Logo, $Z_{tab} = -Z_{0,01} = -2,33$,

pelo fato da distribuição ser simétrica.

Na Figura 10.4 tem-se as regiões de aceitação e rejeição de $H_{0}$ na distribuição de Z.

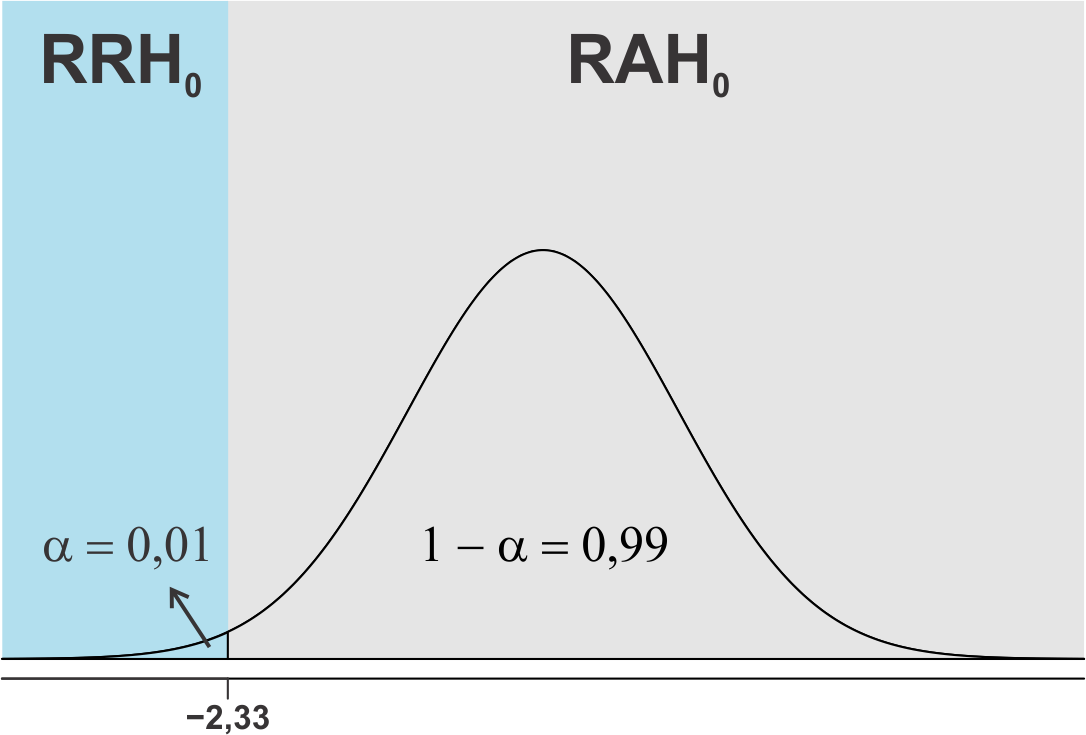
Figura 10.4: Regiões de aceitação e rejeição de $H_0$.

Cálculo do valor do teste através dos dados amostrais utilizando a expressão (10.2). $Z_{c}=\frac{60-70}{\frac{10}{\sqrt{25}}}=-5,0$.
Decisão (Conclusão): $Z_c=-5,0 \in RRH_{0} \Rightarrow$ Rejeita-se $H_{0}:\mu=70$. Logo, aceita-se $H_{a}: \mu < 70$. Portanto, o tempo médio de duração dos enlatados é menor que 70 dias. Diz-se então que o teste foi significativo ao nível de 1,0% de probabilidade.

10.7.2 Pequenas Amostras e Variância Populacional Desconhecida

No caso de pequenas amostras (n < 30), e quando se desconhece a variância populacional $\sigma^2$, o procedimento do teste é dado da seguinte forma:

Formular as hipóteses: $H_0$ e $H_a$. Teste Bilateral: \[\begin{align*} \begin{cases} H_{0}: \mu=\mu_0;\\ H_{a}: \mu \neq \mu_0. \end{cases} \end{align*}\]

Teste Unilateral à Direita: \[\begin{align*} \begin{cases} H_{0}: \mu=\mu_0;\\ H_{a}: \mu > \mu_0. \end{cases} \end{align*}\] Teste Unilateral à Esquerda: \[\begin{align*} \begin{cases} H_{0}: \mu=\mu_0;\\ H_{a}: \mu < \mu_0. \end{cases} \end{align*}\]

Especificar do nível de significância do teste, ou seja o valor de $\alpha$;
Escolha do teste apropriado, estabelecendo a região crítica ($RRH_0$) na distribuição teórica de probabilidades. Neste caso, o teste apropriado é o Teste t, cuja estatística do teste é dada por (10.3). \[ \begin{align} t=\frac{\bar{x}-\mu}{\frac{s}{\sqrt{n}}}, \end{align} \tag{10.3}\] em que $t \sim t_\nu$, isto é, $t$ tem distribuição t-Student com $\nu = n - 1$ graus de liberdade.
Cálculo do valor da estatística do teste através dos dados amostrais, denotado por $t_c$, dado por $\eqref{eq:testet02}$. $$ \[\begin{align} t_{c}=\frac{\bar{x}-\mu_0}{\frac{s}{\sqrt{n}}}, \end{align}\] em que $\mu_0$ é o valor de $\mu$ sob $H_0$.

Em seguida, compara-se o valor de $t_c$ com o valor crítico ($t_{tab}$), consultando a Tabela de t (Tabela $\ref{tab:tdist}$).

Decisão:

DECISÃO \ REALIDADE	\(H_0\) verdadeira	\(H_0\) falsa
Aceitar \(H_0\)	Decisão correta \((1-\alpha)\)	Erro Tipo II \((\beta)\)
Rejeitar \(H_0\)	Erro Tipo I \((\alpha)\)	Decisão Correta \((1-\beta)\)