6 Distribuições de Probabilidades
6.1 Introdução
Cada variável aleatória tem a ela associada uma distribuição de probabilidades, em que se aplica a teoria das probabilidades para descrever seu comportamento. As probabilidades obtidas a partir de um número finito de dados, são conhecidas como probabilidades empíricas. No entanto, distribuições de probabilidades de muitas outras variáveis de interesse, podem ser determinadas baseando-se em considerações teóricas, conhecidas como distribuições teóricas de probabilidades. A seguir, são apresentadas algumas distribuições teóricas de probabilidades, frequentemente usadas para representar a distribuição de probabilidades de variáveis aleatórias.
6.2 Distribuições Discretas de Probabilidades
São distribuições teóricas de probabilidades de variáveis aleatórias discretas, que também são chamadas de modelos discretos de probabilidades.
6.2.1 Distribuição Binomial
Quando um experimento aleatório com apenas dois resultados possíveis, chamado de sucesso ou fracasso, é repetido \(n\) vezes, de forma independente, e a variável aleatória é definida como sendo:cujo o conjunto dos valores possíveis para X são: \(\{ 0, 1, 2, 3,..., n\}\).
Tem-se que a função de probabilidade da variável aleatória X, é dada pela expressão (6.1). \[ \begin{align} P(X = x)=\text{C}_n^x p^x q^{n-x}, x = 0, 1, 2, 3,..., n, \end{align} \tag{6.1}\] em que:
- \(\text{C}_n^x=\frac{n!}{(n-x)!x!} \Rightarrow\) Conta o número de eventos simples do espaço amostral, que resultam em \(x\) sucessos e \(n - x\) fracassos;
- \(p\) é a probabilidade de obter sucesso em uma única tentativa;
- \(q = 1 - p\), é a probabilidade de fracasso em uma única tentativa.
Assim, toda variável aleatória \(X\), cuja função de probabilidade é expressa como (6.1), tem distribuição binomial com parâmetros \(n\) e \(p\). Em notação diz-se: \(X\sim B(n; p)\)1.
A função, \(P(X = x)\), permite calcular a probabilidade de acontecer o resultado \(x\) (números de sucessos) da variável aleatória, não importando a ordem de ocorrência de \(x\) dentro do experimento.
Na distribuição Binomial, a média e a variância são dadas pelas expressões (6.2) e (6.3), respectivamente. \[ \begin{align} E(X)=\mu=np. \end{align} \tag{6.2}\]
\[ \begin{align} V(X)=\sigma^2=npq. \end{align} \tag{6.3}\]
A distribuição Binomial apresenta as seguintes características:
- Em cada experimento a variável aleatória assume apenas dois resultados, sucesso ou fracasso;
- A probabilidade \(p\) do sucesso é constante de experimento para experimento;
- As repetições do experimento são independentes.
Exemplo 6.1 Sabe-se que o poder germinativo das sementes de certa variedade de milho é de 70,0%. Semeando-se dez sementes desta variedade, qual a probabilidade de germinar:
- Nenhuma semente;
- Uma semente;
- Duas sementes;
- Mais de duas sementes.
- Calcule a média, a variância e o desvio padrão.
cujos possíveis valores compreende o conjunto \(\{0, 1, 2, 3, \ldots, 10\}\).
Assim, tem-se:
- \(n=10\);
- \(p=70,0\%=0,7\);
- \(q=1-p=1-0,7=0,3\).
Utilizando-se da expressão (6.1), tem-se que a função de probabilidade da variável aleatória X, é dada por:
\[ P(X = x)=\text{C}_{10}^x0,7^x0,3^{10-x}, x=0, 1, 2, 3, \cdots, 10. \] Logo, pode-se calcular as probabilidades pedidas, como segue: a) \(P(X = 0) = ?\)
\[\begin{align*} P(X = 0) = \text{C}_{10}^{0}0,7^{0}0,3^{10-0}\\ = \frac{10!}{0!(10-0)!} (1)(0,3)^{10}\\ = 1(1)(0,3)^{10}\\ = 0,0000059 = 0,00059\%. \end{align*}\]
- \(P(X = 1) = ?\)
\[\begin{align*} P(X = 1) = \text{C}_{10}^{1}0,7^{1}0,3^{10-1}\\ = \frac{10!}{1!(10-1)!} (0,7)(0,3)^{9}\\ = 10(0,7)(0,3)^{9}= 0,00014 = 0,014\%. \end{align*}\]
- \(P(X = 2)\) = ?
\[\begin{align*} P(X = 2) = \text{C}_{10}^{2}0,7^{2}0,3^{10-2}\\ = \frac{10!}{2!(10-2)!} (0,7)^2(0,3)^{8}\\ = 45(0,7)^2(0,3)^{8}= 0,0015 = 0,15\%. \end{align*}\]
- \(P(X > 2)\) = ?
\[ P(X > 2) = P(X = 3) + P(X = 4) + \cdots + P(X = 10). \] Tem-se que:
\[ P(X = 0) + P(X = 1) + P(X = 2) + \cdots + P(X = 10) = 1,0. \] Logo, \[\begin{align*} P(X > 2) = 1 – [P(X = 0) + P(X = 1) + P(X = 2)]\\ = 1 – [0,0000059 + 0,00014 + 0,0015]\\ = 1 – 0,0017\\ = 0,9983 = 99,83\%. \end{align*}\]
- Utilizando-se das expressões (6.2) e (6.3), respectivamente, a média e a variância são dadas por:
\(E(X)=\mu=10(0,7)=7\) sementes, e\(V(X)=\sigma^2=10(0,7)(0,3)=2,1~(\textrm{sementes})^2\) . O desvio padrão é dado por:
Exemplo 6.2 No nascimento de dois bezerros de vacas diferentes, qual é a probabilidade de nascer duas fêmeas?
Tem-se que a variável aleatória representa o sucesso:cujos possíveis valores de X compreende o conjunto: \(\{0, 1, 2\}\). Assim, tem-se:
- \(n=2\);
- \(p=50,0\%=0,5\);
- \(q=1-p=1-0,5=0,5\).
Utilizando-se da expressão (6.1), tem-se que a função de probabilidade da variável aleatória \(X\), é dada por: \[ P(X = x)=\text{C}_2^x0,5^x0,5^{2-x}, \quad x=0, 1, 2. \] Logo, a probabilidade pedida é dada por: \[\begin{align*} P(X = 2) = \text{C}_{2}^{2}0,5^{2}0,5^{2-2}\\ = \frac{2!}{2!(2-2)!}(0,5)^{2}(0,5)^0\\ = 1(0,5)^2(1)= 0,25 = 25,0\%. \end{align*}\]
6.2.2 Distribuição de Poisson
Na distribuição binomial, quando o número \(n\) tende para infinito, e a probabilidade do sucesso \(p\) tende para zero, ficando o produto \(np\) finito e não-nulo, ela é aproximada pela distribuição de Poisson.
A funcão de probabilidade da distribuição de Poisson é dada pela expressão (6.4). \[ \begin{align} P(X = x)=\frac{e^{-\mu} \mu^x}{x!}, x=0, 1, 2, 3, \ldots, \end{align} \tag{6.4}\] sendo:
- \(e\) a base dos logaritmos neperianos, igual a \(2,7183...\);
- \(\mu\) a média da distribuição, dada por: \(\mu=np\).
Assim, toda variável aleatória X, cuja função de probabilidade é expressa como (6.4), tem distribuição de Poisson com parâmetro \(\mu\). Em notação diz-se: X \(\sim Poisson(\mu)\)2.
Na distribuição de Poisson, tem-se que a média e a variância são dadas pelas expressões (6.5) e (6.6), respectivamente. \[ \begin{align} E(X)=\mu=np, \end{align} \tag{6.5}\] e \[ \begin{align} V(X)=\sigma^2=np. \end{align} \tag{6.6}\] Uma característica importante na distribuição de Poisson, é que a média é igual a variância.
Exemplo 6.3 A probabilidade de que um pintinho apresente uma reação após a aplicação de uma vacina é de 0,2%. Um lote de 2.000 pintinhos receberam a vacina. Qual a probabilidade de ter reação:
- Dois pintinhos;
- No máximo quatro pintinhos;
- Pelo menos dois pintinhos.
cujos possíveis valores de X compreende o conjunto: \(\{0, 1, 2, 3, \ldots, 2.000\}\).
Assim, tem-se que:
- \(n=2.000\);
- \(p=0,2\%=0,002\);
- \(\mu=np=2.000(0,002)=4,0\).
Utilizando-se a expressão (6.4), a função de probabilidade da variável aleatória X, é dada por:
\[ P(X = x)=\frac{e^{-4,0}4,0^x}{x!}, x=0, 1, 2, 3, \cdots, 2.000. \]
Logo, o cálculo das probabilidade pedidas são dadas por:
- \(P(X = 2) = ?\)
\[ P(X = 2)=\frac{e^{-4,0}4,0^2}{2!}=0,1465 = 14,65\%; \]
- \(P(X \leq 4)= ?\)
\[ P(X \leq 4) =P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3) + P(X = 4); \]
- \(P(X = 0)=\frac{e^{-4,0}4,0^0}{0!}=0,0183 = 1,83\%\);
- \(P(X = 1)=\frac{e^{-4,0}4,0^1}{1!}=0,0733 = 7,33\%\);
- \(P(X = 3)=\frac{e^{-4,0}4,0^3}{3!}=0,1954 = 19,54\%\);
- \(P(X = 4)=\frac{e^{-4,0}4,0^4}{4!}=0,1954 = 19,54\%\).
Logo, \[\begin{align*} P(X \leq 4) = 0,0183 + 0,0733 + 0,1465 + 0,1954 + 0,1954\\ = 0,6289 = 62,89\%. \end{align*}\]
- \(P(X \geq 2)= ?\)
\[ P(X \geq 2) = P(X = 2) + P(X = 3) + \cdots + P(X = 2.000). \] Tem-se que: \[ P(X = 0) + P(X = 1) + P(X = 2) + \cdots + P(X = 2.000) = 1,0. \] Logo, \[\begin{align*} P(X \geq 2) = 1 – [P(X = 0) + P(X = 1)]\\ = 1 – [0,0183 + 0,0733]\\ = 1 – 0,0916\\ = 0,9084 = 90,84\%. \end{align*}\]
6.3 Distribuições Contínuas de Probabilidades
São distribuições teóricas de probabilidades de variáveis aleatórias contínuas, que também são chamadas de modelos contínuos de probabilidades. Existem diversos modelos contínuos, mas neste capítulo será dado ênfase apenas a distribuição Normal, apresentada a seguir.
6.3.1 Distribuição normal
A distribuição de frequências de uma amostra de dados, geralmente apresenta uma maior concentração dos dados ao redor de um valor central. Quando os dados se afastam deste valor central a concentração diminui. Esta característica chama-se tendência central dos dados, sendo mais evidente em dados de variáveis aleatórias contínuas.
Aumentando-se o tamanho da amostra e a precisão das medidas desses dados, a representação gráfica da distribuição de frequências tenderá a ser uma curva em forma de sino, simétrica em relação ao ponto de frequência máxima, com aspecto semelhante ao da Figura 6.1. Esta curva chama-se curva normal ou de Gauss, e representa a distribuição de frequências da população, sendo, portanto, uma curva teórica.
Várias variáveis aleatórias contínuas seguem este padrão em suas distribuições de frequências, que podem ser descritas pela distribuição normal.
A distribuição normal apresenta a seguinte função densidade de probabilidade, dada por (6.7). \[ \begin{align} f(x)=\frac{1}{\sqrt{2\pi\sigma^2}}e^\frac{-(x-\mu)^2}{2\sigma^2}, -\infty < x < \infty, \end{align} \tag{6.7}\] em que:
- \(\pi=3,1416...\);
- \(e\) é a base dos logaritmos neperianos, igual a \(2,7183...\);
- \(\mu\) a média da distribuição, em que: \(-\infty < \mu < \infty\);
- \(\sigma^2\) a variância da distribuição, em que: \(\sigma^2 > 0\).
A distribuição normal é descrita pelos parâmetros: \(\mu\) e \(\sigma^2\) (média e variância), isto é, \[\begin{align*} E(X)=\mu \textrm{ e } V(X)=\sigma^2. \end{align*}\]
Os valores da variável X são representados no eixo horizontal, e a média de X é a projeção sobre o eixo do ponto de frequência máxima da curva. Em notação diz-se: X \(\sim N(\mu; \sigma^2)\).
A família de curvas normais é bastante grande. Na realidade existe uma curva normal para cada par de valores de \(\mu\) e \(\sigma^2\). As diferenças em \(\mu\) deslocam a curva para a direita ou para a esquerda sobre o eixo \(x\). Já um valor alto de \(\sigma^2\) tem por efeito estender a curva sobre uma amplitude maior e, em consequência, a curva fica achatada. Ao passo que um valor baixo de \(\sigma^2\), a curva torna-se contraída e alta no centro (afilada).
6.3.1.1 Características da Distribuição Normal
A Distribuição Normal apresenta as seguintes características:
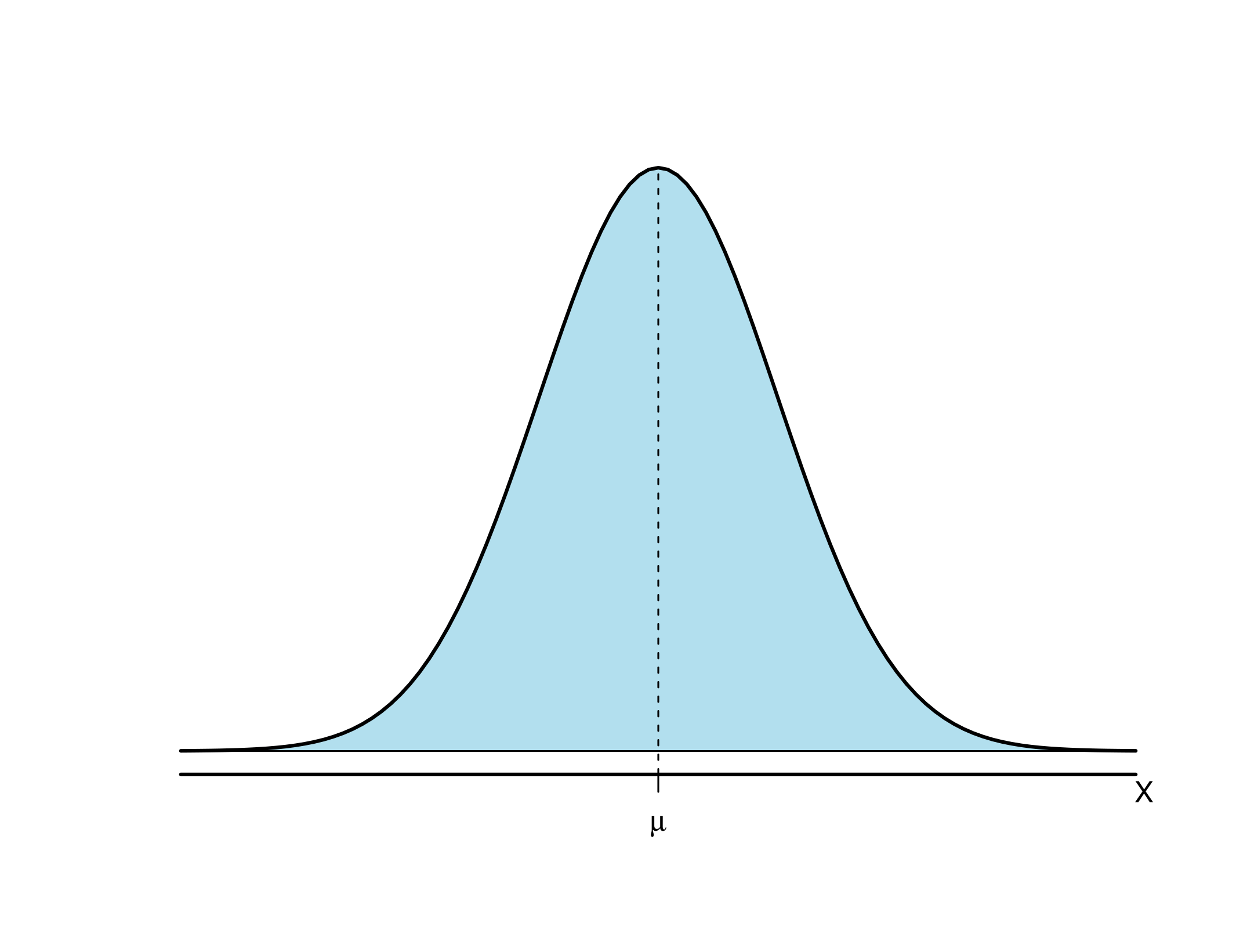
- É simétrica ao redor da média \(\mu\), conforme Figura 6.2;
- As três medidas de posição se coincidem, ou seja, \(\mu = Md = Mo\);
- Fica definida conhecendo-se os valores de \(\mu\) e \(\sigma^2\). Conhecendo-se \(\mu\) e \(\sigma^2\) acha-se a ordenada \(f(x)\) para qualquer valor de \(x\);
- A área total compreendida sob a curva e o eixo \(x\) é igual a 1,0, ou seja, trata-se de uma função densidade de probabilidade legítima. \[ \int_{-\infty}^{\infty} f(x) \, dx=\int_{-\infty}^{\infty} \frac{1}{\sqrt{2\pi\sigma^2}}e^\frac{-(x-\mu)^2}{2\sigma^2} \, dx=1,0. \]
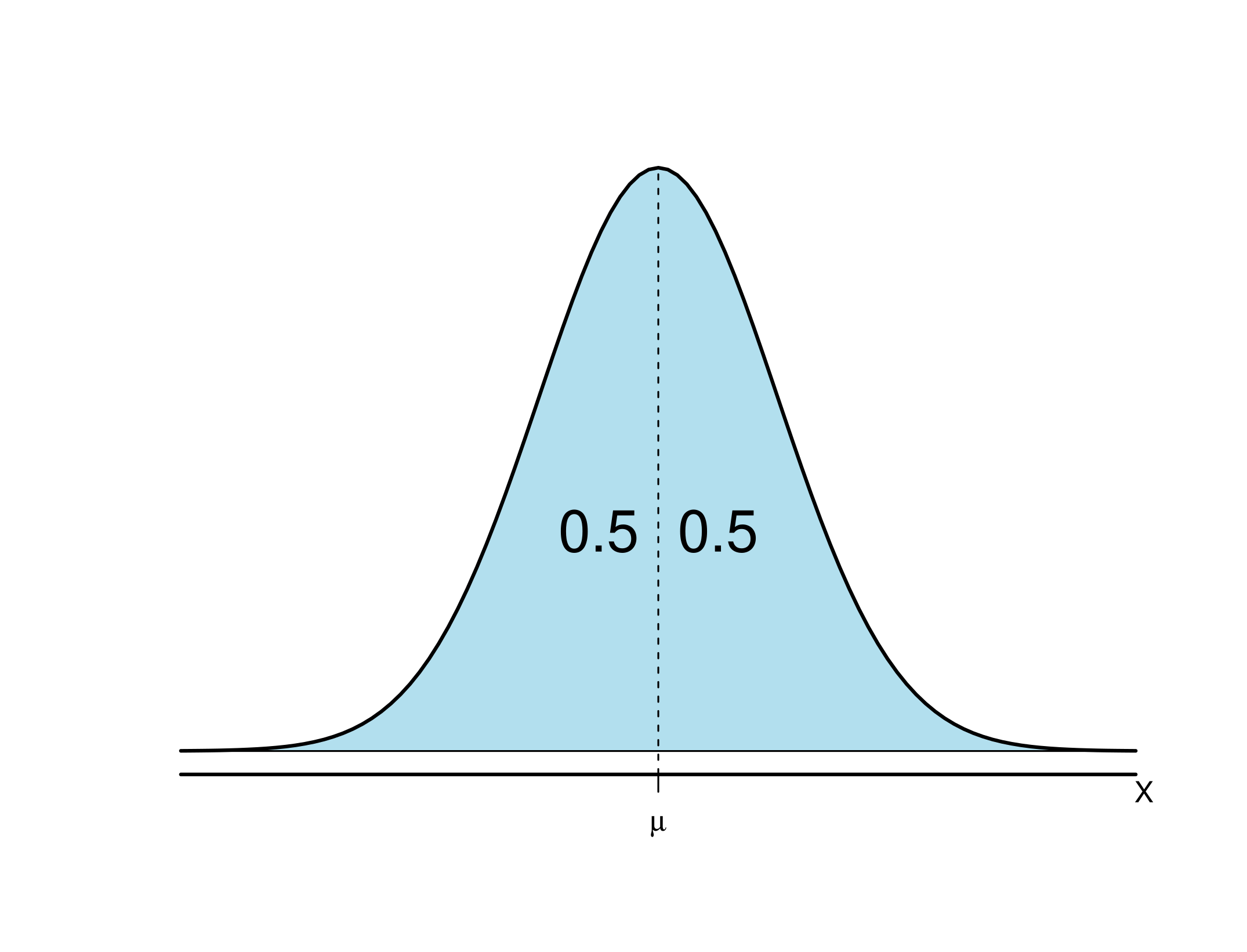
Sendo a distribuição simétrica, 50,0% da área se encontram de ambos os lados da média, conforme Figura 6.3.
- É assintótica em relação ao eixo \(x\). Se \(x\) cresce ou decresce, \(y\) decresce mas sem chegar a zero;
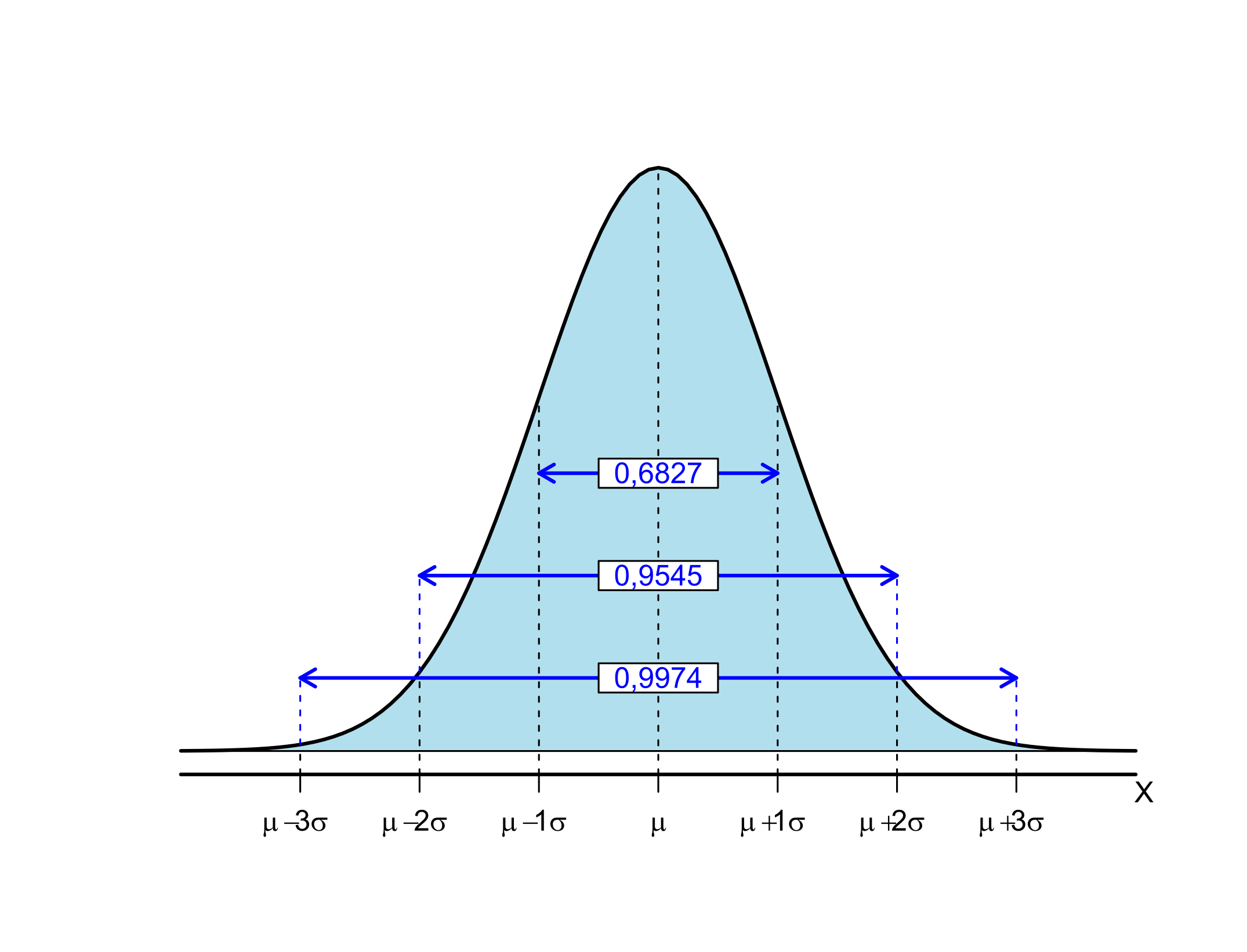
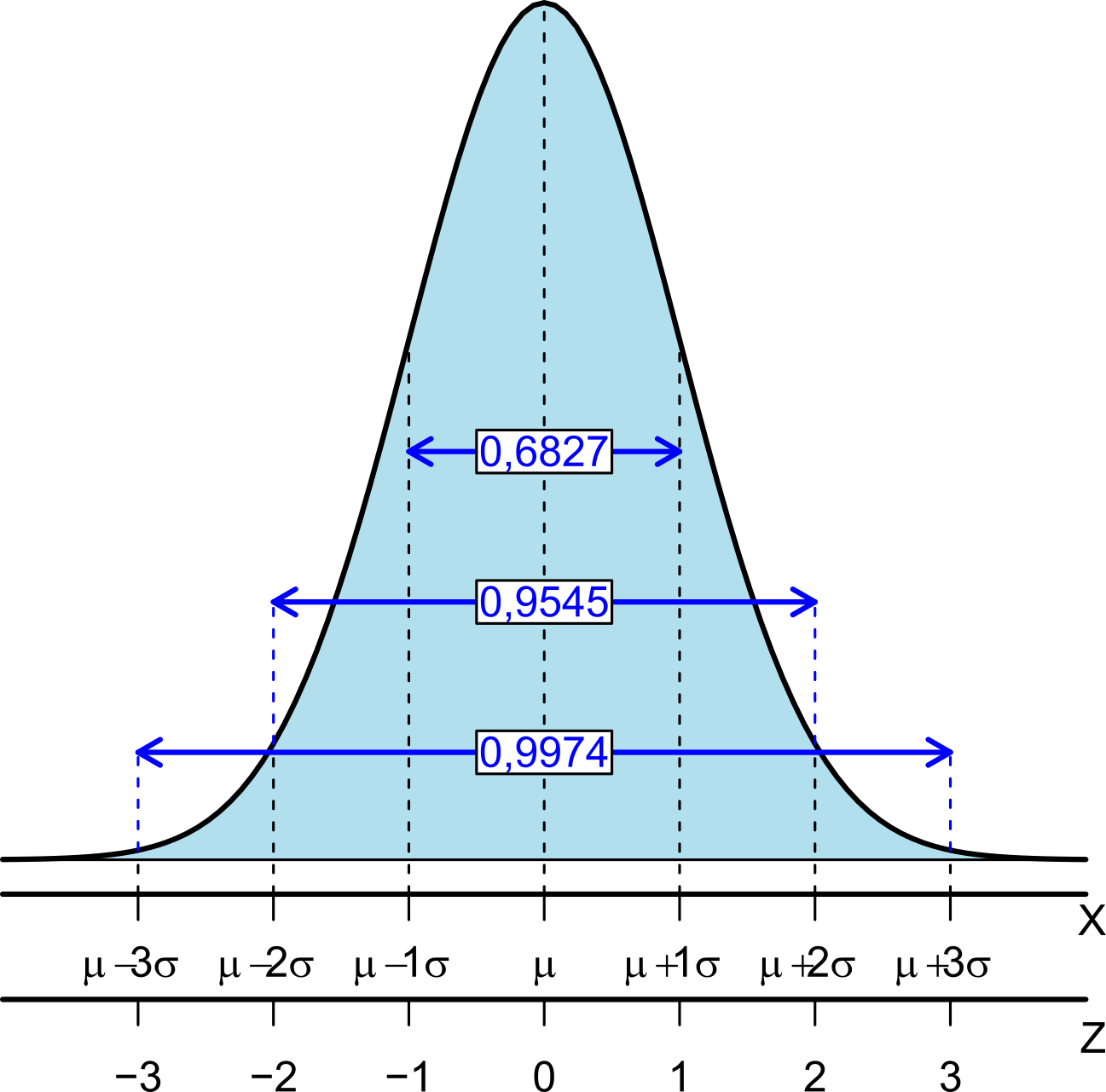
- A área sob a curva, de acordo com a Figura 6.4, entre:
- \(\mu \pm \sigma\) corresponde a 68,27% da área total;
- \(\mu \pm 2\sigma\) corresponde a 95,45% da área total;
- \(\mu \pm 3\sigma\) corresponde a 99,74% da área total.
O estudo da distribuição normal é um dos mais importantes em Estatística, pois na maioria dos casos, os métodos estatísticos que serão vistos adiante, pressupõem que os dados sejam provenientes de uma distribuição normal.
6.3.1.2 Cálculo de Probabilidades na Distribuição Normal
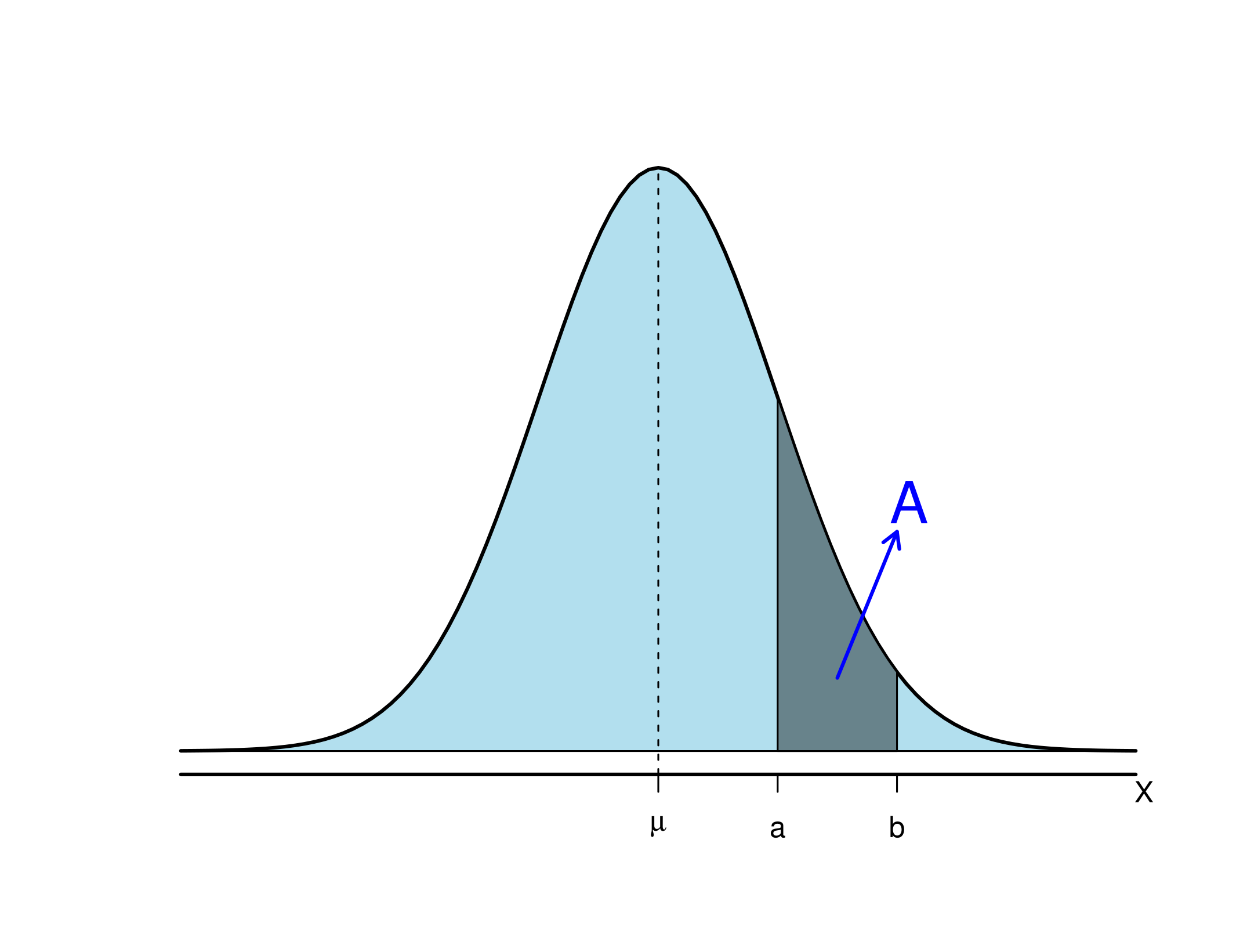
A área A, representada pela Figura 6.5, compreendida entre duas ordenadas levantadas sobre dois pontos a e b do eixo x da curva normal, expressa a probabilidade da variável aleatória X, assumir valores no intervalo (a, b).
Logo, a área A pode ser calculada por:
\[ A = P(a < x < b) = \int_{a}^{b} f(x) \, dx=\int_{a}^{b} \frac{1}{\sqrt{2\pi\sigma^2}}e^\frac{-(x-\mu)^2}{2\sigma^2} \, dx. \]
A solução dessa integral é um processo complexo, não sendo, portanto, de fácil solução. Assim, é necessário fazer uso de um procedimento alternativo.
Devido a grande aplicação prática da distribuição normal em Estatística, procurou-se construir uma tabela para valores de integração, conforme a que está indicada para a área A (Figura 6.5). Como existe uma série infinita de curvas normais, representativas de distribuições normais de probabilidades, cada uma especificada pelos valores que \(\mu\) e \(\sigma^2\) assumem em cada caso particular, esse tabelamento encontrou dificuldades.
Assim, torna-se necessário uma padronização, adotando-se uma distribuição normal comum como referência, transformando os valores reais em relativos. A distribuição de referência, chamada de distribuição normal reduzida ou distribuição normal padronizada, é aquela em que a média é igual a \(0,0\) e o desvio padrão igual a \(1,0\). Assim, qualquer distribuição normal com média diferente de \(0,0\) e desvio padrão diferente de \(1,0\), pode ser transformada na distribuição normal padronizada.
A transformação aplicada a cada valor de X, é feita através da obtenção de uma nova variável, denominada de Z, dada pela expressão (6.8). \[ \begin{align} Z=\frac{X-\mu}{\sigma}, \end{align} \tag{6.8}\] em que:
- \(Z\) é o afastamento dos valores de \(X\) em relação à média em número de desvios padrão;
- \(X\) é a variável aleatória com distribuição normal com parâmetros \(\mu\) e \(\sigma^2\);
- \(\mu\) é média da distribuição;
- \(\sigma\) é o desvio padrão da distribuição.
Em notação diz-se: Z \(\sim N(0,0; 1,0)\)3
A Figura 6.6 apresenta a correspondência entre X e Z.
Os valores da distribuição normal padronizada, referentes à área (probabilidade) acumulada para diferentes valores de Z, podem ser encontrados em tabelas, não havendo assim a necessidade de serem calculadas. A Tabela A 1 especifica a área (probabilidade) compreendida entre \(0,0\) e um valor de Z maior que zero. Já a Tabela A 2 representa a probabilidade tal que \(P(Z > z)\), em que \(z > 0,0\).
Exemplo 6.4 Seja uma variedade de milho, onde a altura (X) é uma variável aleatória, que segue a distribuição normal de média \(200,0\) cm e variância \(100,0\) \(\textrm{cm}^2\). Qual a probabilidade de uma planta dessa variedade ter altura:
- entre \(190,0\) e \(195,0\) cm?
- maior que \(190,0\) cm?
- menor que \(190,0\) cm?
Tem-se que:
\[ X \sim N(200,0; 100,0), \] em que:
- \(\mu=200,0\) cm;
- \(\sigma^2=100,0~\textrm{cm}^2 \Rightarrow \sigma=\sqrt{100,0}=10,0\) cm.
As probabilidades pedidas são dadas a seguir.
- \(P(190,0 < X < 195,0) = ?\)
Utilizando-se da expressão (6.8), os valores de \(Z\) correspondentes a \(x=190,0\) e \(x=195,0\), são dados por:
- para \(x=190,0 \Rightarrow Z_1=\frac{190,0-200,0}{10,0}=-1,0\);
- para \(x=195,0 \Rightarrow Z_2=\frac{195,0-200,0}{10,0}=-0,5\).
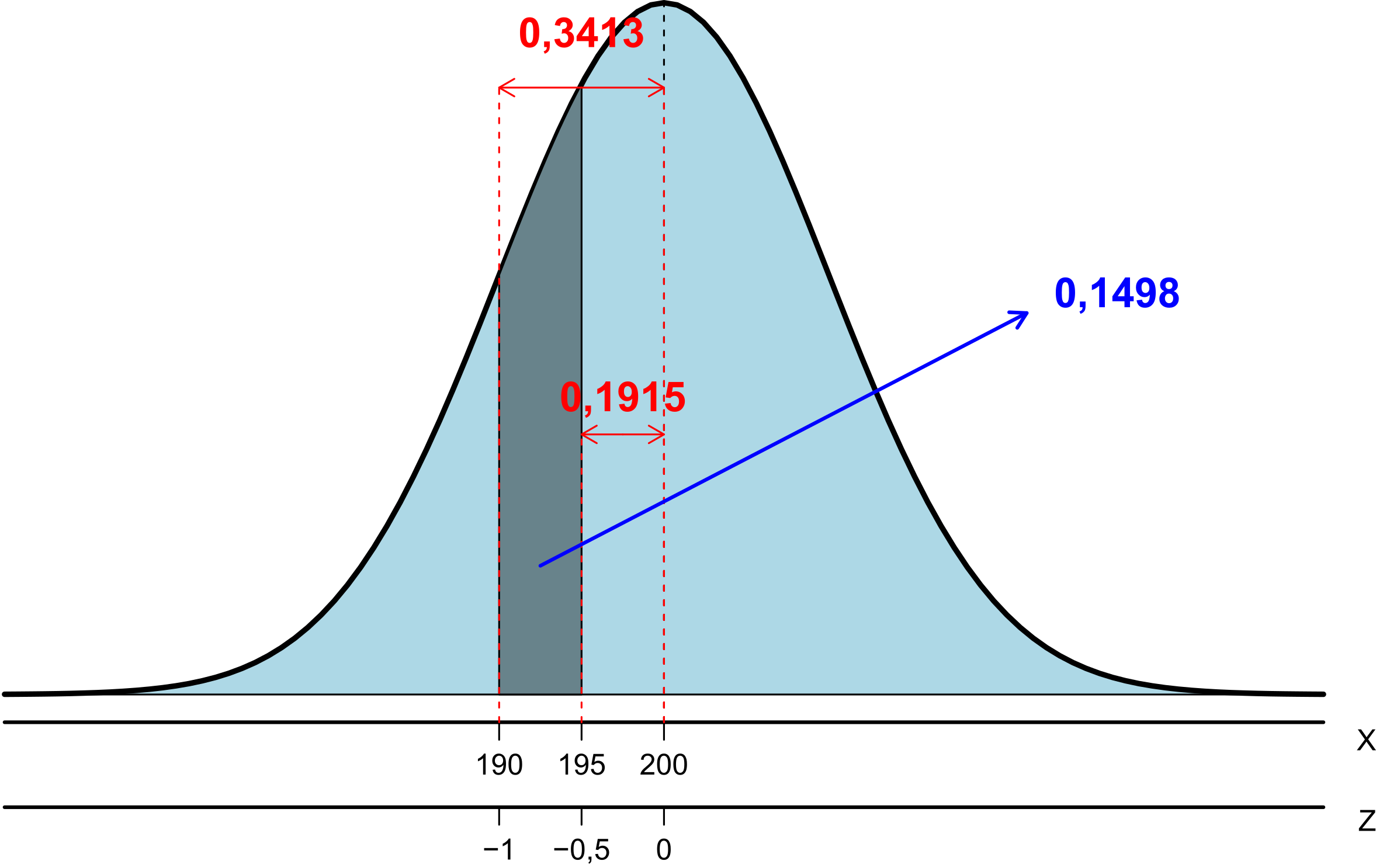
Consultando a Tabela A 1, tem-se que a área (probabilidade) compreendida para o intervalo de Z estar entre \(0,0\) e \(1,0\) é igual a \(0,3413\) (consulta-se o valor \(1,0\) na primeira coluna e \(0,00\) na linha superior da tabela e cruza os dois valores), e para o intervalo de Z estar entre \(0,0\) e \(0,5\) é igual a \(0,1915\) (consulta-se o valor \(0,5\) na primeira coluna e \(0,00\) na linha superior da tabela e cruza os dois valores), conforme esquema abaixo:

Assim, tem-se por simetria que: \[ P(-0,5 < Z < 0,0)=P(0,0 < Z < 0,5)=0,1915, \] e \[ P(-1,0 < Z < 0,0)=P(0,0 < Z < 1,0)=0,3413. \] Logo, tem-se que: \[\begin{align*} P(190,0 < X < 195,0) = P(-1,0 < Z < -0,5)\\ = P(-1,0 < Z < 0,0)-P(-0,5 < Z < 0,0)\\ = 0,3413-0,1915\\ = 0,1498=14,98\%. \end{align*}\]
A representação gráfica desse cálculo de probabilidade pode ser verificada na Figura Figura 6.7.
- \(P(X > 190,0) = ?\)
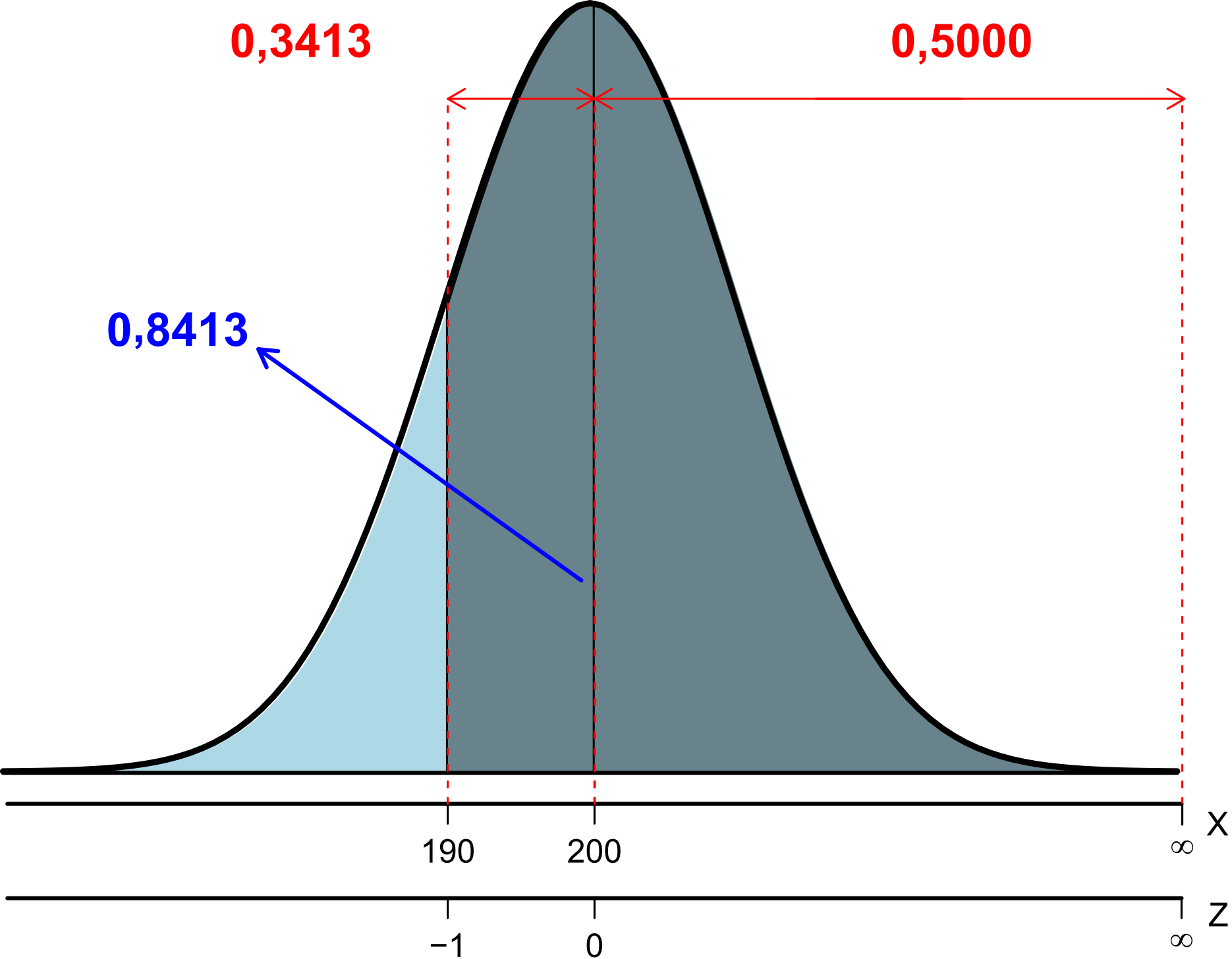
\[\begin{align*} P(X > 190,0) = P(Z > -1,0) = P(-1,0 < Z < 0,0) + 0,5\\ = 0,3413 + 0,5 = 0,8413 = 84,13\%. \end{align*}\]
Sendo que a representação gráfica pode ser observada na Figura 6.8.
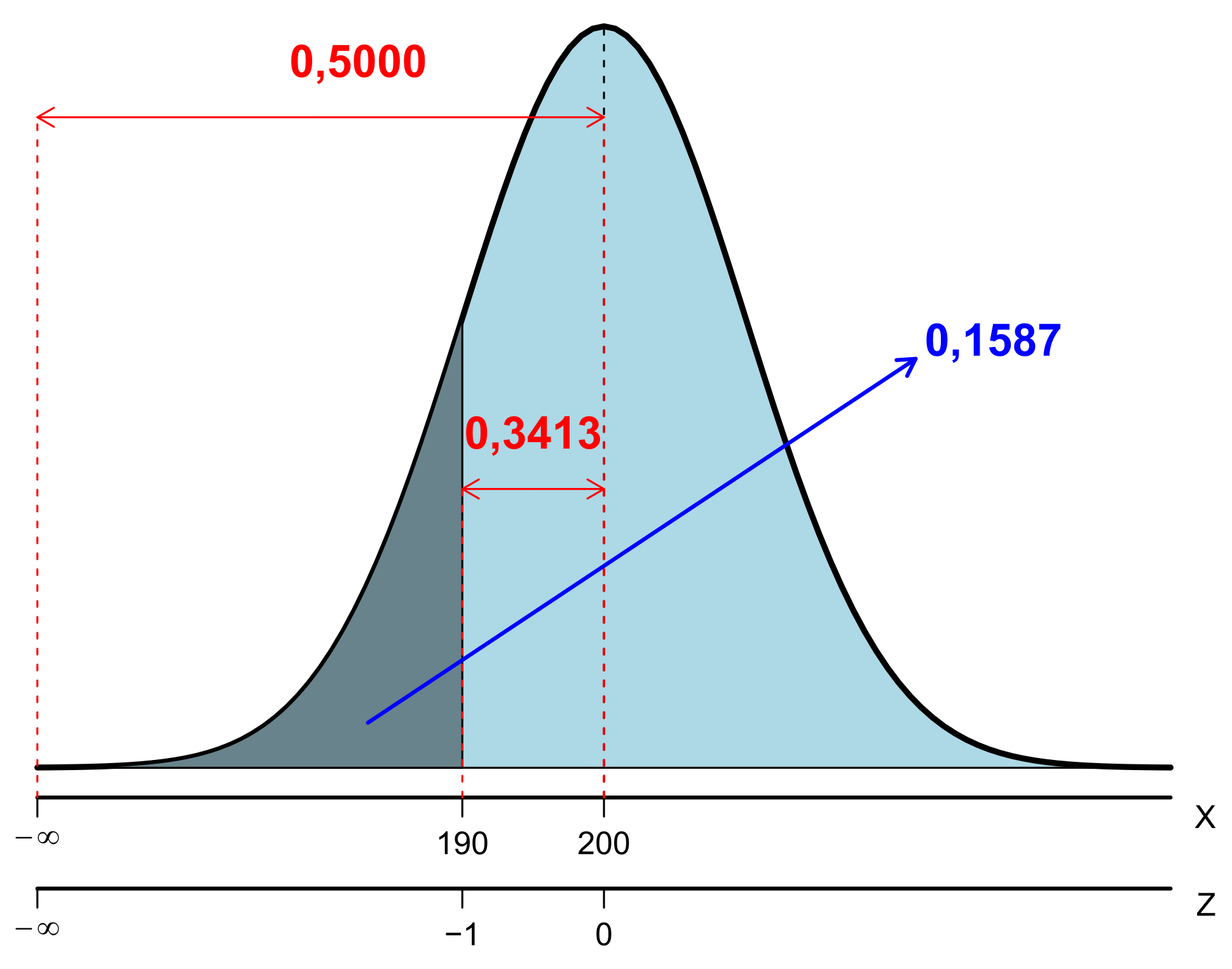
- \(P(X < 190,0) = ?\)
\[\begin{align*} P(X < 190,0) = P(Z < -1,0) = 0,5 - P(-1,0 < Z < 0,0)\\ = 0,5 - 0,3413 = 0,1587 = 15,87\% \end{align*}\]
Onde a representação gráfica pode ser observada na Figura 6.9.
Exemplo 6.5 A variável aleatória X, que representa a precipitação anual, em mm, na cidade de Ouro Branco, MG, segue uma distribuição normal de probabilidades, com média igual a 1.529,7 mm e variância igual a 53.777,61 \(\textrm{mm}^2\). Calcule:
- A probabilidade de que não chova mais de \(1.500,0\) mm;
- A probabilidade de que chova mais de \(1.800,0\) mm;
- A probabilidade de que chova entre 1.400,0 e 1.600,0 mm;
- O valor da precipitação anual tal que apenas \(5,0\)% dos anos supera.
Tem-se que: \[ X \sim N(1.529,7; 53.776,61), \] em que:
- \(\mu=1.529,7\) mm;
- \(\sigma^2=53.776,61~ \textrm{mm}^2 \Rightarrow \sigma=\sqrt{53.776,61}=231,9\) mm.
As probabilidades pedidas são dadas a seguir.
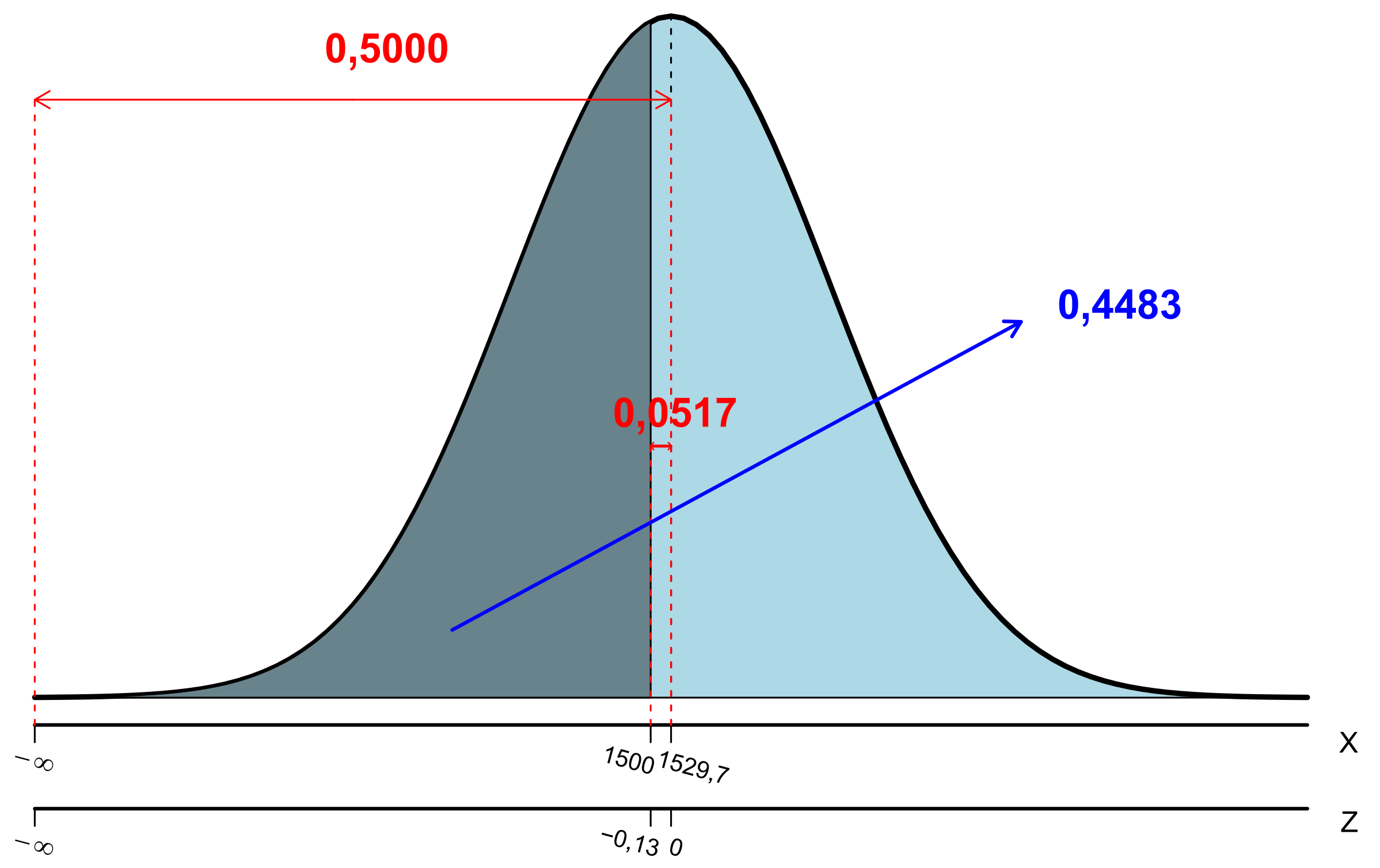
- \(P(X \leq 1.500,0)=?\)
Utilizando-se a expressão (6.8), o valor de Z correspondente a \(x=1.500,0\) é dado por: \[ Z=\frac{1.500,0-1.529,7}{231,9}=-0,13. \]
Consultando a Tabela A 1, tem-se que a área (probabilidade) compreendida para o intervalo de Z estar entre \(0,0\) e \(0,13\) é igual a \(0,0517\) (consulta-se o valor \(0,1\) na primeira coluna e \(0,03\) na linha superior da tabela e cruza os dois valores), conforme esquema abaixo:
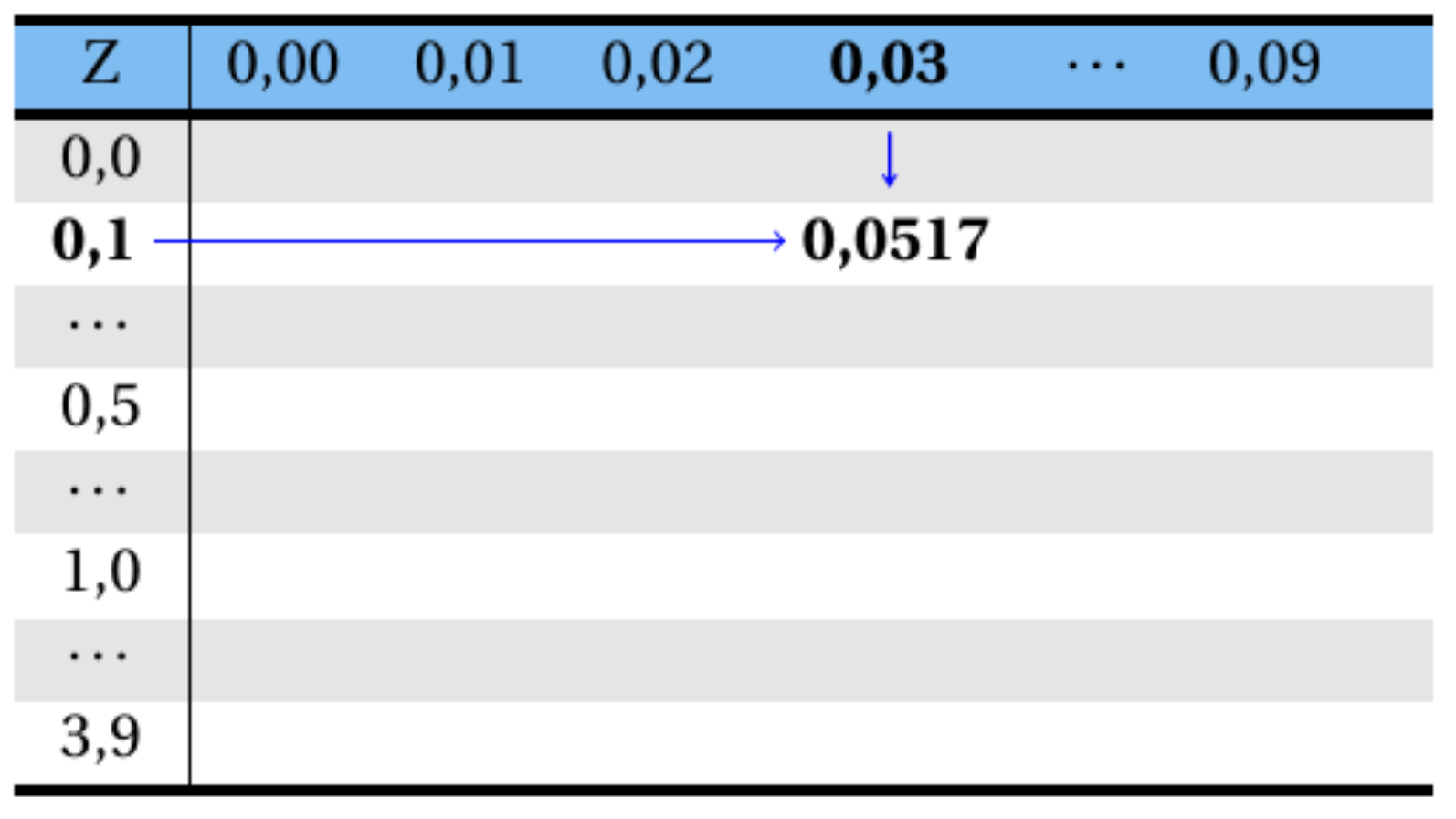
Assim, tem-se por simetria que:
\[ P(-0,13 < Z < 0,0)=P(0,0 < Z < 0,13)=0,0517. \]
Logo, tem-se que: \[\begin{align*} P(X \leq 1.500,0) = P(Z<-0,13) =0,5-P(-0,13 < Z < 0,0)\\ =0,5-0,0517=0,4483=44,83\%. \end{align*}\]
Sendo que a sua representação gráfica pode ser observada pela Figura 6.10.
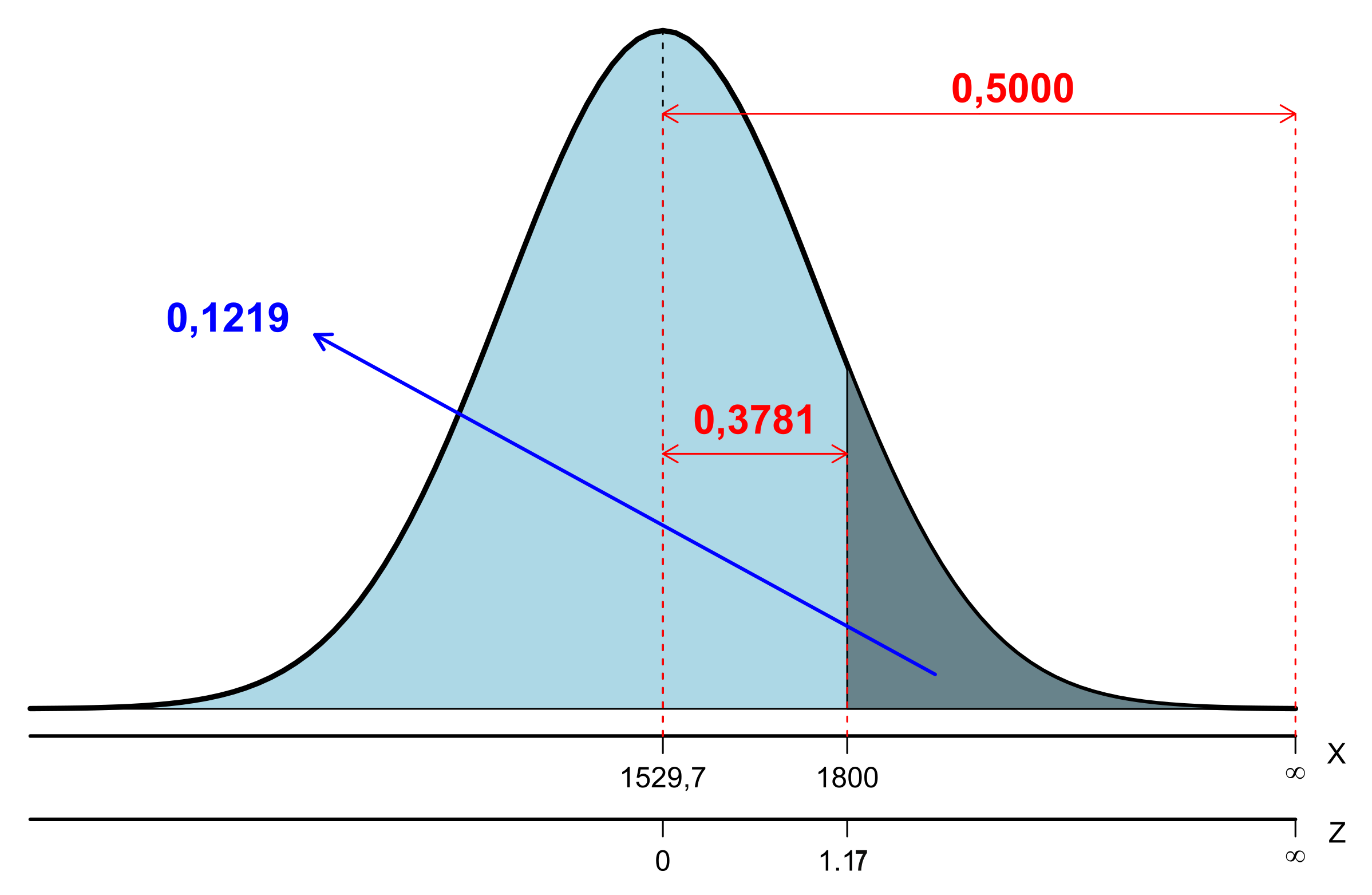
- \(P(X>1.800,0)=?\)
Utilizando-se da expressão (6.8), o valor de Z correspondente a \(x=1.800,0\), é dado por: \[ Z=\frac{1.800,0-1.529,7}{231,9}=1,17. \]
Consultando a Tabela A 1, tem-se que a área (probababilidade) compreendida para o intervalo de Z estar entre \(0,0\) e \(1,17\) é igual a \(0,3790\) (consulta-se o valor \(1,1\) na primeira coluna e \(0,07\) na linha superior da tabela e cruza os dois valores), conforme esquema abaixo:
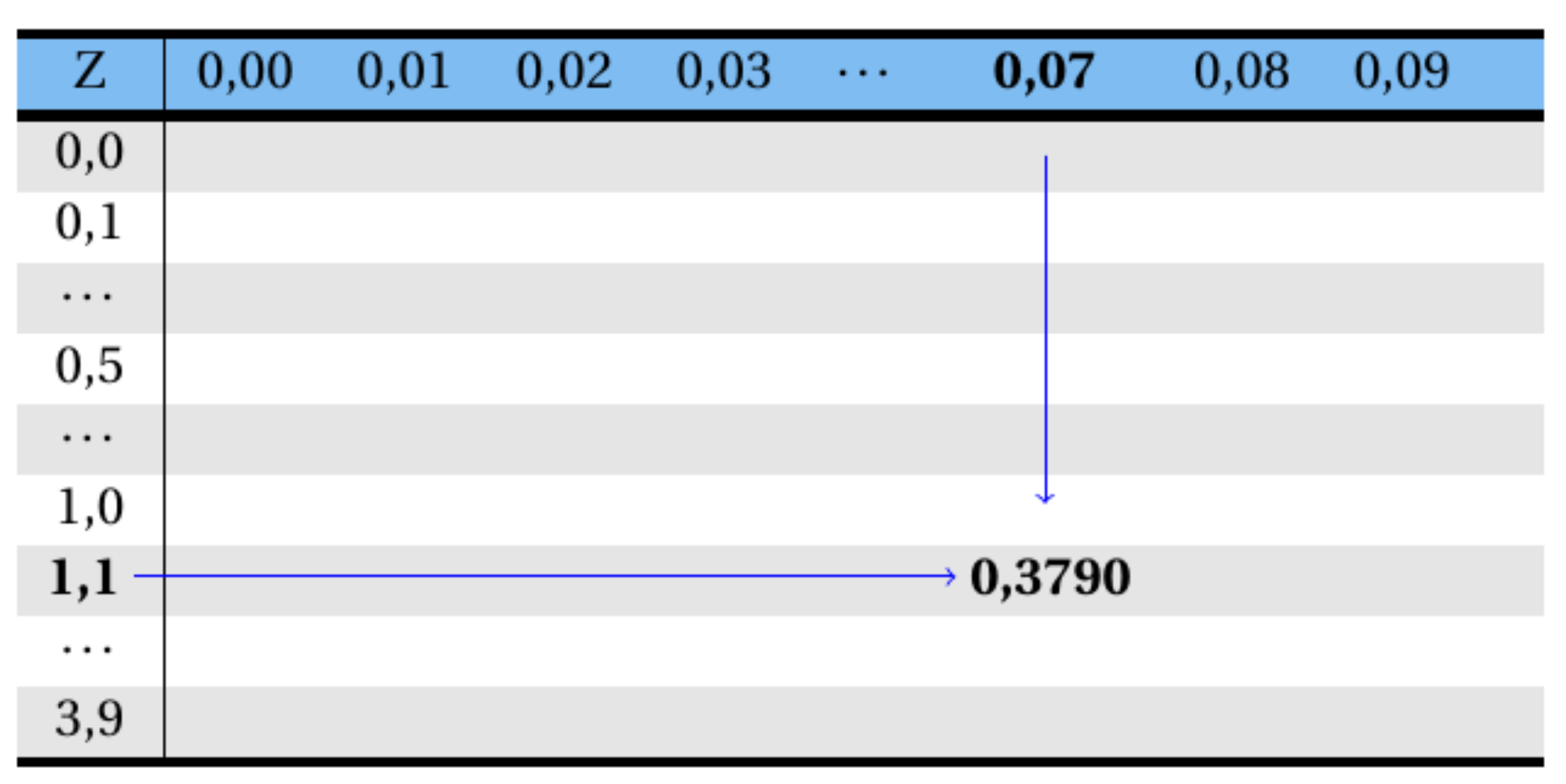
Assim, tem-se que: \[ P(0,0 < Z < 1,17)=0,3790. \] Logo, \[\begin{align*} P(X>1.800,0)=P(Z>1,17) = 0,5-P(0,0 < Z < 1,17)\\ | =0,5-0,3790=0,1210=12,10\%. \end{align*}\]
A representação gráfica desta probabilidade pode ser observada pela Figura 6.11.
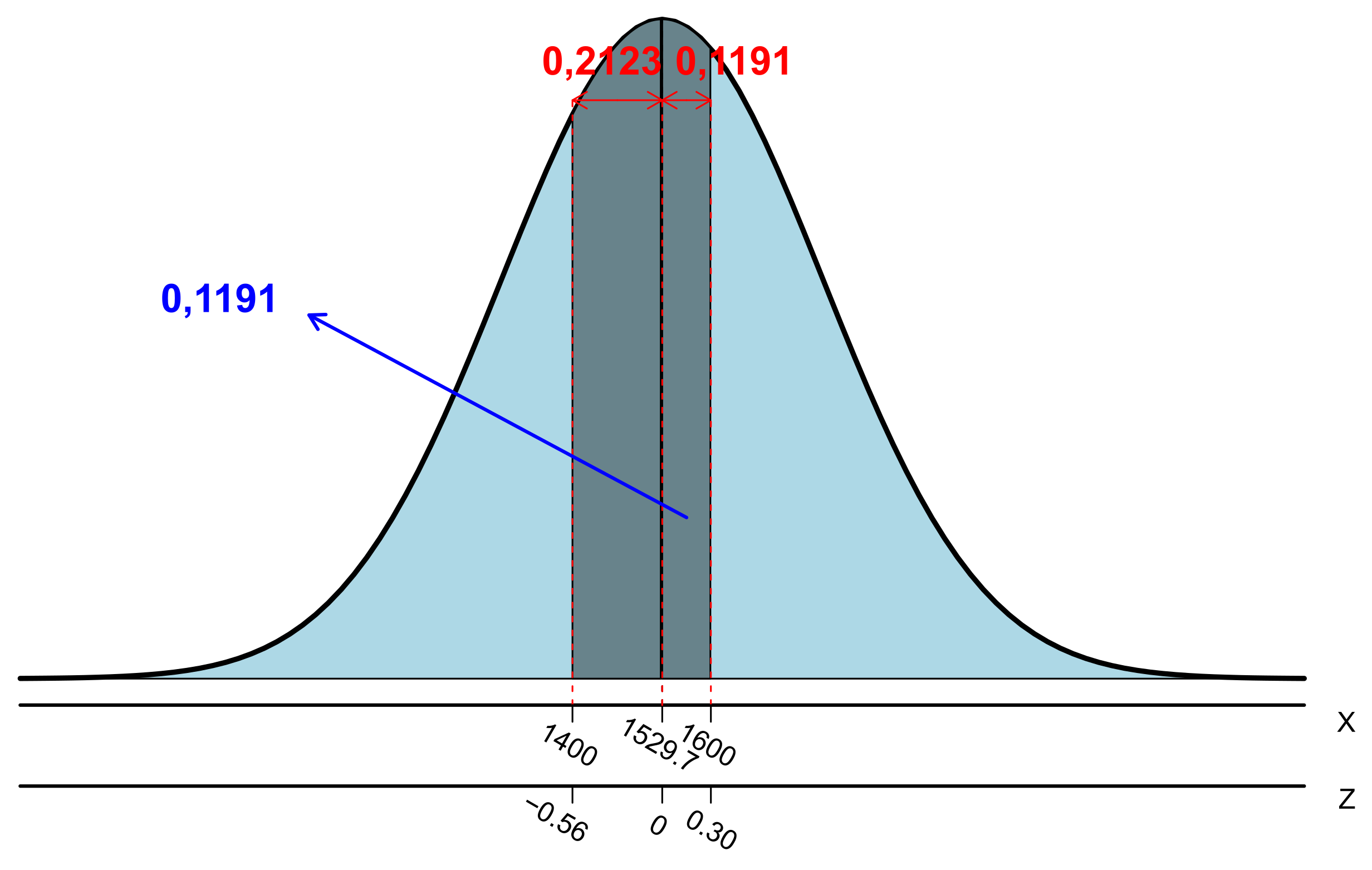
- \(P(1.400,0 < X < 1.600,0)\) = ?
Utilizando-se da expressão (6.8), os valores de Z correspondentes a \(x=1.400,0\) e \(x=1.600,0\), são dados por:
- Para \(x=1.400,0 \Rightarrow Z=\frac{1.400,0-1.529,7}{231,9}=-0,56\);
- Para \(x=1.600,0 \Rightarrow Z=\frac{1.600,0-1.529,7}{231,9}=0,30\).
Consultando a Tabela A 1, tem-se que a área (probabilidade) compreendida para o intervalo de Z estar entre \(0,0\) e \(0,56\) é igual a \(0,2123\) (consulta-se o valor \(0,5\) na primeira coluna e \(0,06\) na linha superior da tabela e cruza os dois valores), e para o intervalo de Z estar entre \(0,0\) e \(0,30\) é igual a \(0,1179\) (consulta-se o valor \(0,3\) na primeira coluna e \(0,00\) na linha superior da tabela e cruza os dois valores), conforme esquema abaixo:
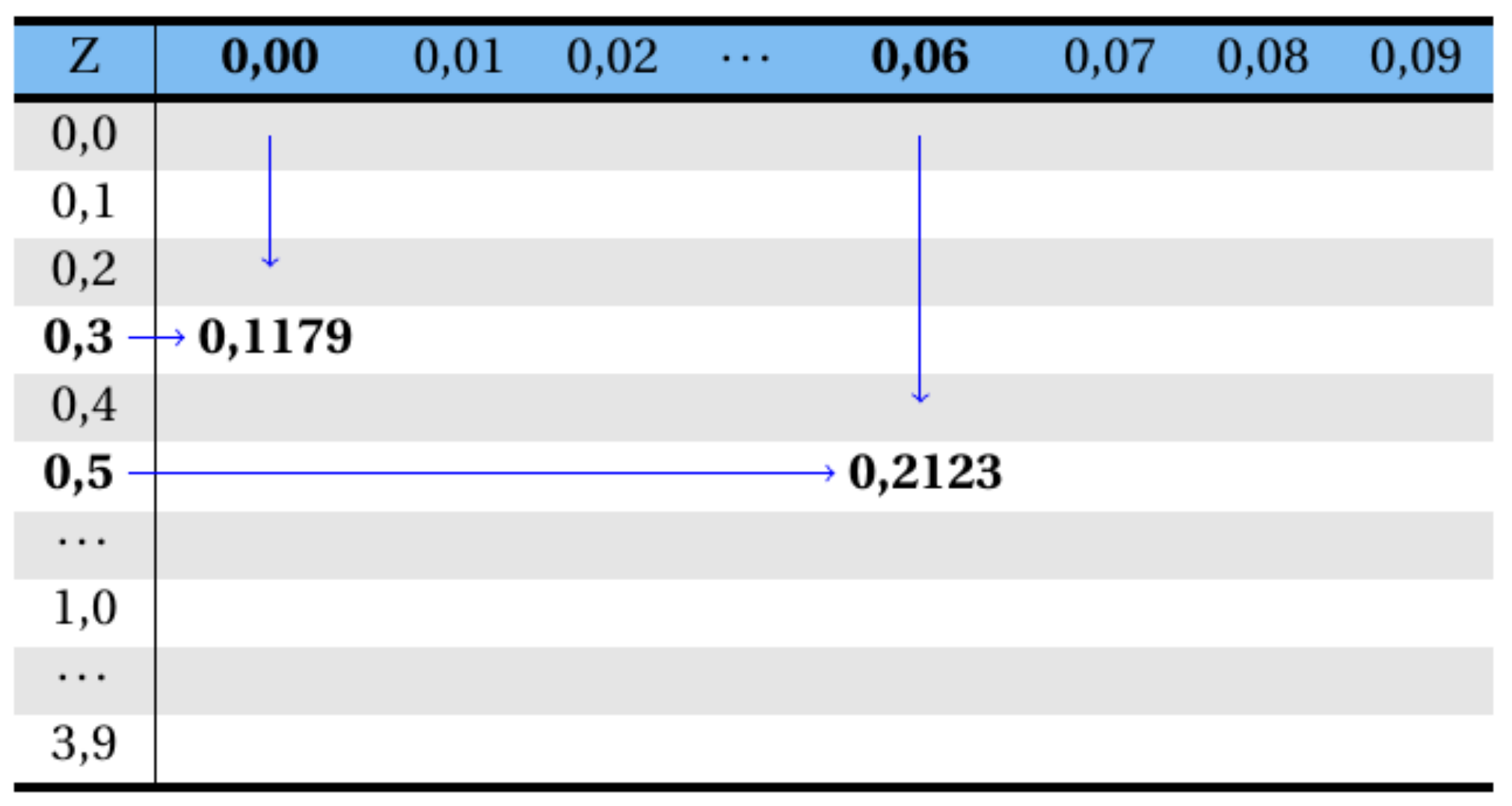
Assim, tem-se por simetria que: \[ P(-0,56 < Z < 0,0)=P(0,0 < Z < 0,56)=0,2123. \] e, \[ P(0,0 < Z < 0,30)=0,1179. \] Logo, \[\begin{align*} P(1.400,0 < x < 1.600,0) = P(-0,56 < Z < 0,30)\\ = P(-0,56 < Z < 0,0) + P(0,0 < Z < 0,30)\\ = 0,2123 + 0,1179=0,3302 = 33,02\%, \end{align*}\]
Sendo que sua representação gráfica pode ser verificada na Figura 6.12.
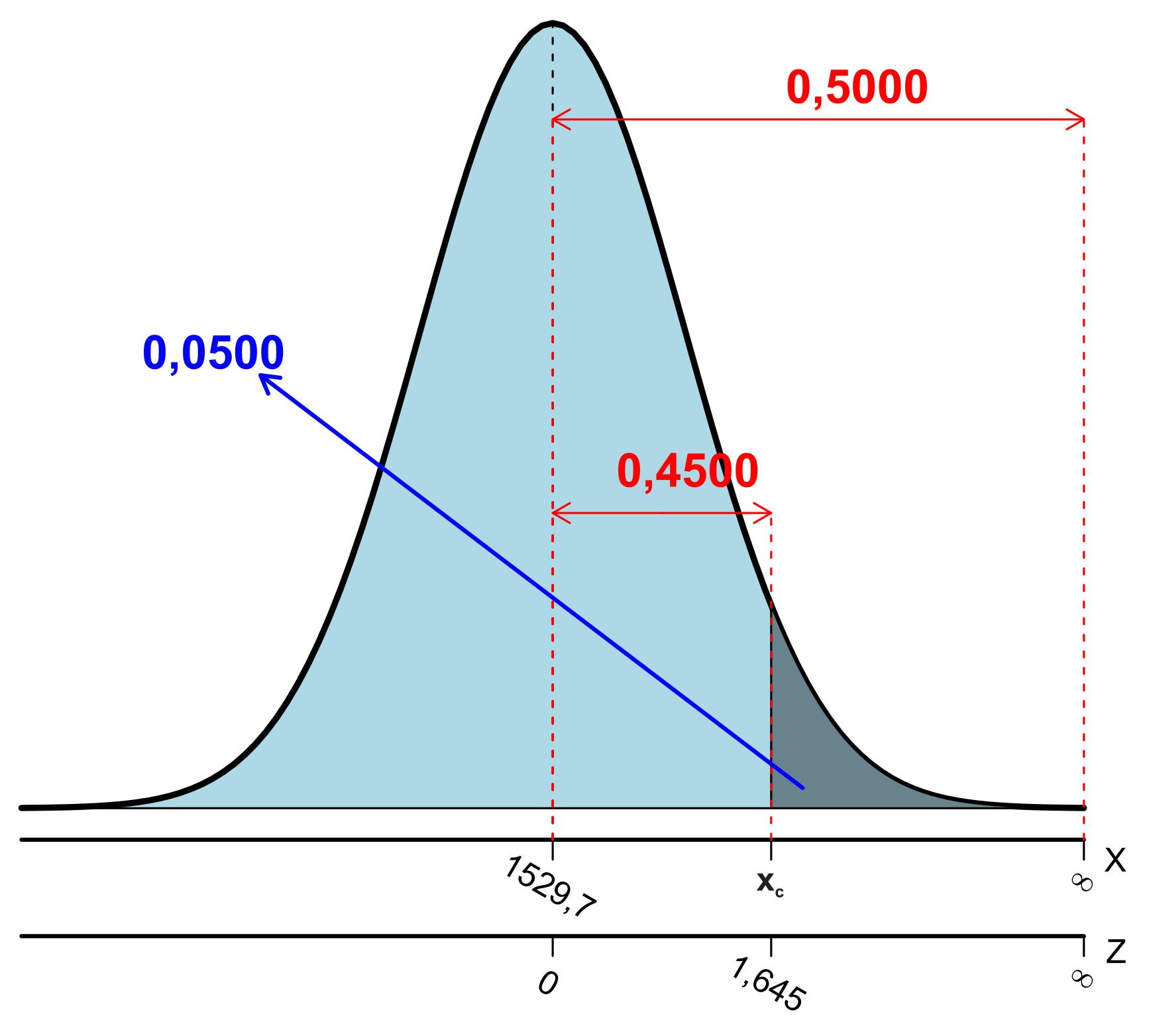
\(P(X>x_{c})=5,0\%=0,05 \Rightarrow x_{c}=?\)
Tem-se que a área (probabilidade) correspondente a distribuição normal padronizada acima de \(0,0\) é igual a \(0,50\). Assim o valor de Z desejado deve corresponder a uma área de \(0,45\) (\(0,50- 0,05\)). Consultando a Tabela A 1, o valor de Z que corresponde a uma área (probabilidade) de \(0,45\) é igual a \(1,645\) (média de \(1,64\) e \(1,65\)). Consulta-se dentro do corpo da tabela o valor referente a \(0,45\), conforme esquema abaixo:
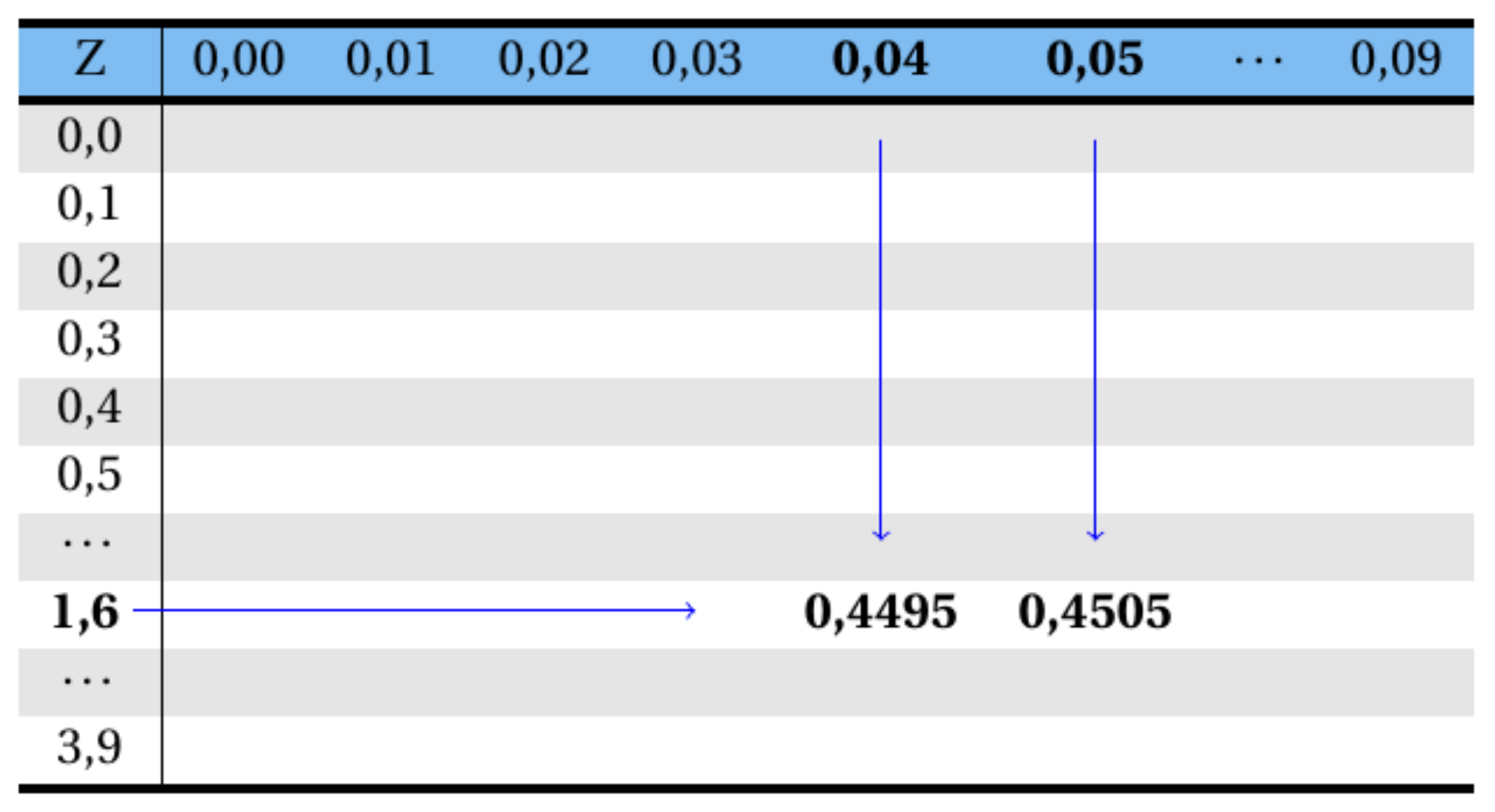
\[ \frac{0,4495+0,4505}{2}=0,45 \Rightarrow Z=\frac{1,64+1,65}{2}=1,645. \] Tem-se que: \[ Z=\frac{x-\mu}{\sigma}. \] Assim, \[ 1,645=\frac{x_c-1.529,7}{231,9} \Rightarrow x_c=1.911,1755~\textrm{mm}. \] Logo, o valor de X que deixa uma probabilidade acima dele de \(5,0\%\) é igual a: \(x_c = 1.911,1755\) mm, conforme Figura 6.13.
6.3.1.3 Aproximação Normal das Distribuições Binomial e de Poisson
A distribuição normal também pode ser utilizada como uma aproximação, para o cálculo de probabilidades envolvendo as distribuições binomial e de Poisson.
Exemplo 6.6 A probabilidade de uma planta de certa variedade de feijão ser resistente à ferrugem é de 0,25. Numa amostra de 40 plantas desta variedade, qual a probabilidade de se ter 14 plantas sadias.
Considere a variável aleatória X que representa o sucesso:cujos possíveis valores de X compreende o conjunto: \(\{0, 1, 2, \cdots, 40\}\).
Tem-se que:
- \(n = 40\);
- \(p = 0,25\);
- \(q = 1 -p = 1 - 0,25 = 0,75\).
Utilizando-se a expressão (6.1), a função de probabilidade da variável aleatória \(X\), é dada por: \[ P(X = x)=\text{C}_{40}^{x}0,25^{x}0,75^{40-x}, x=0, 1, 2, \cdots, 40. \]
A probabilidade pedida é dada por: \[\begin{align*} P(X = 14) = \text{C}_{40}^{14}0,25^{14}0,75^{40-14}\\ = \frac{40!}{14!(40-14)!}(0,25)^{14}(0,75)^{26}\\ = 0,0488 = 4,88\%. \end{align*}\]
Suponha agora que se deseja calcular a probabilidade de ser ter mais de 14 plantas sadias. Tem-se então que: \[\begin{align*} P(X > 14) = P(X = 15) + P(X = 16) + \cdots + P(X = 40)\\ = 1 – P(X \leq 14). \end{align*}\]
Como se vê esta probabilidade é bastante trabalhosa de ser calculada.
Os problemas envolvendo as distribuições binomial e de Poisson, exigem cálculos trabalhosos quando n é muito grande, como ocorre no Exemplo 6.6. Uma alternativa, seria utilizar a distribuição normal como uma aproximação dessas distribuições, tornando esta aproximação cada vez melhor quanto maior for n.
No uso da aproximação normal, deve-se lembrar que as Distribuições Binomial e de Poisson são discretas (só existe a probabilidade de valores inteiros), e a distribuição normal é contínua (existe a probabilidade de qualquer valor real avaliada em intervalos). Por essa razão, deve-se usar uma correção de continuidade, que consiste em considerar a probabilidade de um valor de X estar no intervalo: \(x_i - 0,5\) e \(x_i + 0,5\).
Exemplo 6.7 Considerando o Exemplo 6.6, tem-se:
- \(\mu=np=40(0,25)=10,0\);
- \(\sigma^2=npq=40(0,25)(0,75)=7,5\);
- \(\sigma=\sqrt{7,5}=2,74\).
Assim, \[ P(X = 14) \cong P(13,5 < X < 14,5) = ?. \] Utilizando-se a expressão (6.8), os valores de Z correspondentes a \(x=13,5\) e \(x=14,5,0\), são dados por:
- Para \(x=13,5 \Rightarrow Z=\frac{13,5-10,0}{2,74}=1,28\);
- Para \(x=14,5 \Rightarrow Z=\frac{14,5-10,0}{2,74}=1,64\).
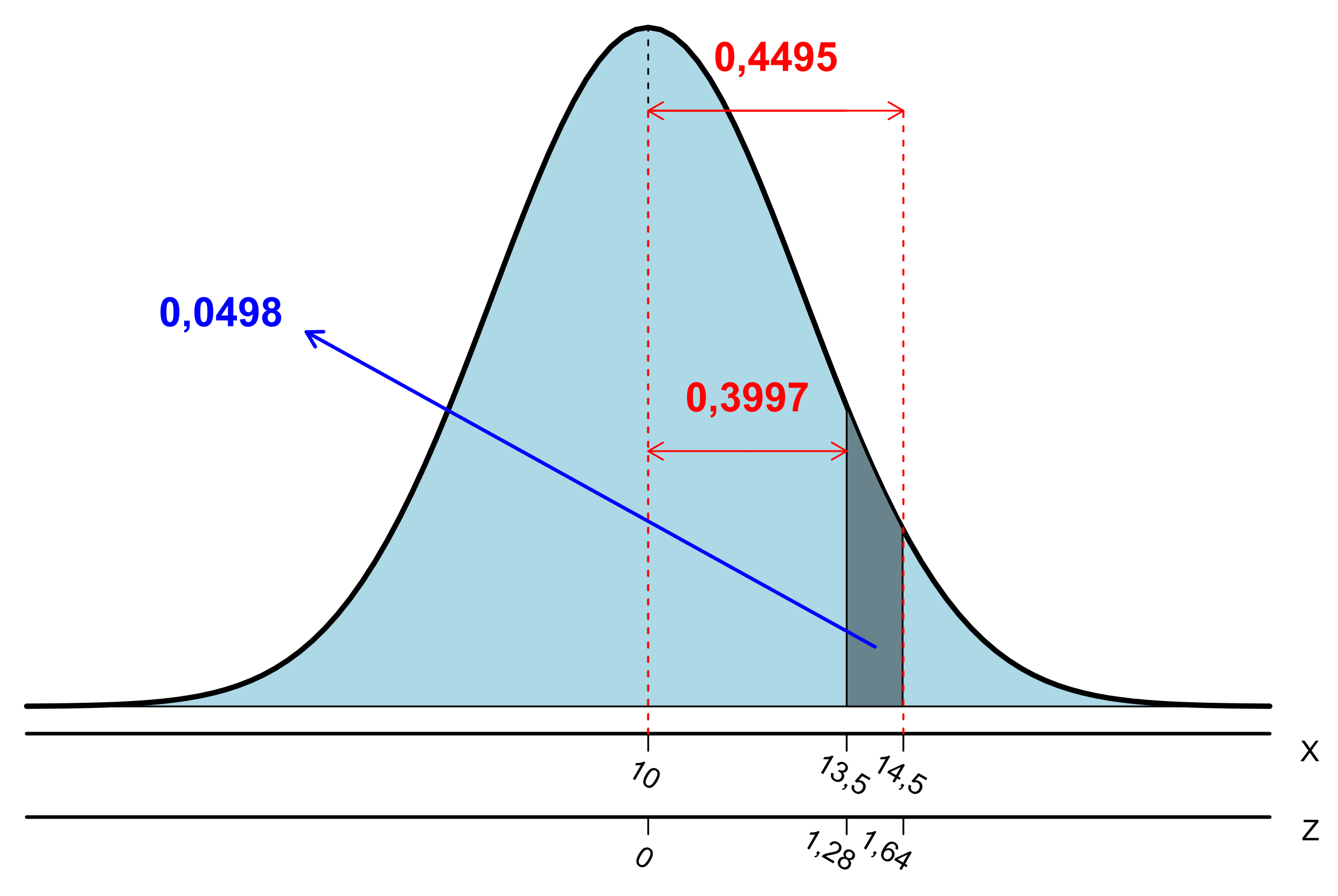
Consultando-se a Tabela A 1, a área (probabilidade) compreendida para o intervalo de Z estar entre \(0,0\) e \(1,28\) é igual a \(0,3997\) (consulta-se o valor \(1,2\) na primeira coluna e \(0,08\) na linha superior da tabela e cruza os dois valores), e para o intervalo de Z estar entre \(0,0\) e \(1,64\) é igual a \(0,4495\) (consulta-se o valor \(1,6\) na primeira coluna e \(0,04\) na linha superior da tabela e cruza os dois valores), conforme esquema abaixo:
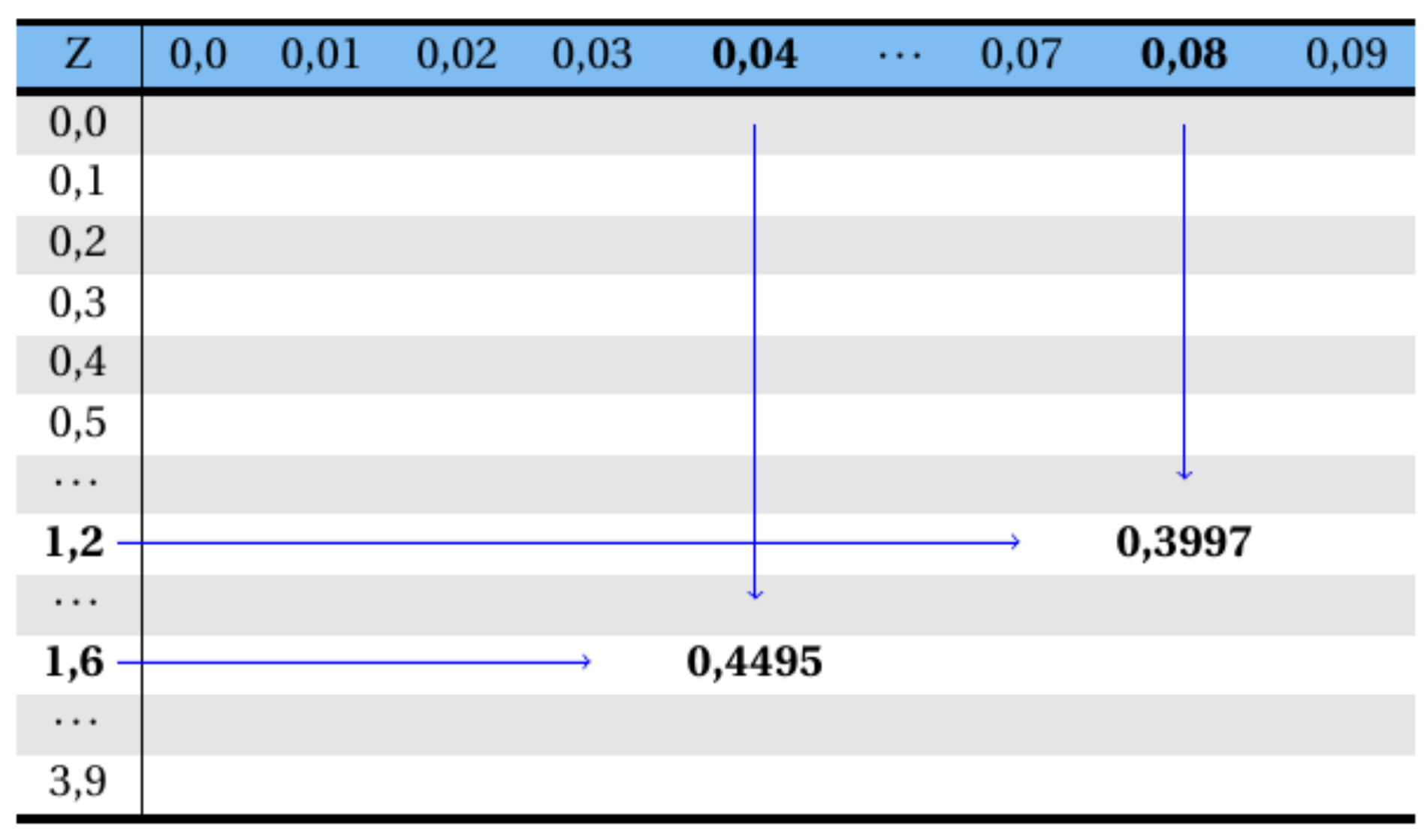
Logo, \[ P(0,0 < Z < 1,28)=0,3997, \] e \[ P(0,0 < Z < 1,64)=0,4495. \]
Assim, tem-se que: \[\begin{align*} P(13,5 < X < 14,5) = P(1,28 < Z < 1,64)\\ = P(0,0 < Z < 1,64) - P(0,0 < Z < 1,28)\\ = 0,4495 - 0,3997 = 0,0498 = 4,98\%. \end{align*}\]
Cuja representação gráfica pode ser verificada na Figura 6.14.
Mostrando assim a qualidade da aproximação.
A probabilidade de se ter mais de 14 plantas sadias pode, então, ser calculada por: \[\begin{align*} P(X > 14) |\cong P(Z > 1,64) = 0,5 - P(0,0 < Z < 1,64)\\ | \cong 0,5 - 0,4495 = 0,0505 = 5,05\%. \end{align*}\]
Resumindo, a aproximação das Distribuições Binomial e Poisson à Normal, são baseadas nas transformações:
- Distribuição Binomial: \[ P(X=x) \cong P(Z_1 < Z < Z_2). \]
- Distribuição de Poisson:
6.4 Outras Distribuições de Probabilidades
Existem várias outras distribuições de probabilidades, tanto discretas como contínuas, que não serão abordadas aqui. No caso discreto tem-se as distribuições: Uniforme discreta, Bernoulli, Geométrica, Hipergeométrica, Binomial Negativa. E no caso contínuo as distribuições: Uniforme contínua, Exponencial, Gama, Beta, Weibull. Outras distribuições contínuas importantes \((t, qui-quadrado, F)\) serão vistas no Capítulo 8.
Exercícios propostos
Exercício 6.1 Sabe-se que 5,0% de um rebanho bovino está com febre aftosa. Qual a probabilidade de que num lote de seis animais retirados deste rebanho tenha-se:
- Nenhum animal com febre aftosa;
- Um animal com febre aftosa;
- Dois animais com febre aftosa;
- Mais de um animal com febre aftosa;
- Calcule a média e a variância.
Exercício 6.2 Um veterinário está estudando o índice de natalidade em suínos sujeitos à inseminação artificial. Ele sugeriu que a variável X: número de filhotes nascidos vivos, poderia ser ajustada pela distribuição binomial com parâmetros \(n = 10\) e \(p = 0,5\).
- Preencha a tabela abaixo:
| \(x\) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| \(P(X = x)\) |
- Calcule a média e a variância de \(X\).
Exercício 6.3 Suponha que a porcentagem de germinação de sementes de feijoeiros seja de 60,0%. Vão ser semeadas duas sementes por cova. A disposição das covas no canteiro está apresentado no esquema abaixo:

em que o “círculo escuro” representa uma cova.
Qual é a probabilidade de obter-se no máximo 18 covas que não falham no canteiro?
Exercício 6.4 A probabilidade de ser necessária a correção da acidez em solos de uma região é de 60,0%. Encomendou-se a análise de solos em 50 talhões de terra em propriedades desta região. Qual é a probabilidade de que mais de 30 talhões necessitem de calagem (correção da acidez).
Exercício 6.5 Suponha que a probabilidade de que um tubérculo colhido por uma colheitadeira seja danificado pela máquina é de 10,0%. Se 10 tubérculos colhidos por essa máquina são selecionados ao acaso, qual é a probabilidade de que não mais do que um tubérculo danificado seja encontrado.
Exercício 6.6 A probabilidade de ocorrer uma planta híbrida de citrus a partir de uma semente advinda de polinização controlada é de 20%. Com cinco sementes: a) Qual é a probabilidade de se obter pelo menos uma planta híbrida; b) Qual é o número de plantas híbridas que se espera obter com as cinco sementes.
Exercício 6.7 Sabe-se que em média existem 200 larvas de um inseto prejudicial a uma lavoura de milho, a cada 2.000 litros de água num córrego próximo a lavoura. Qual é a probabilidade de que numa amostra de um litro de água retirada deste córrego existam pelo menos uma larva.
Exercício 6.8 Examinaram-se 2.000 ninhadas de cinco suínos cada uma, segundo o número de machos. Os dados estão representados na tabela abaixo:
| Número de machos (\(X\)) | Número de ninhadas | |
|---|---|---|
| 0 | 20 | |
| 1 | 360 | |
| 2 | 700 | |
| 3 | 680 | |
| 4 | 200 | |
| 5 | 40 | |
| Total | 2.000 |
- Calcule a proporção média de machos;
- Calcule para cada valor de X, o número de ninhadas que você deve esperar se: X \(\sim B (5, p)\), onde \(p\) é a proporção média de machos calculada em (a).
Exercício 6.9 Um Engenheiro Agrícola querendo prever o comportamento pluviométrico de uma região, com o objetivo de elaborar um projeto de drenagem, encontra um estudo realizado, no qual aponta-se que a variável aleatória X: número de chuvas por ano acima de 40,0 mm/h, é descrita por uma distribuição de Poisson com parâmetro \(\mu=1,7\).
- Preencha a tabela abaixo:
| \(x\) | 0 | 1 | 2 | 3 | 4 ou mais |
| \(P(X = x)\) |
- Qual o número médio de chuvas por ano acima de 40,0 mm/h.
Exercício 6.10 Uma vacina apresenta uma eficiência de 99,98% na imunização de bovinos contra a febre aftosa. Todos os animais de um rebanho de 10.000 cabeças foram vacinados. Qual a probabilidade de que neste rebanho:
- Um animal tenha febre aftosa;
- No mínimo um animal apresente febre aftosa.
Exercício 6.11 Usando a tabela da distribuição normal padronizada (Tabela A 1) determine as seguintes áreas (probabilidades) com representação gráfica:
- Entre 0,0 e 1,32;
- Entre 0,17 e 1,28;
- Entre -0,92 e 1,64;
- Abaixo de 1,20;
- À esquerda de -0,84;
- Acima de 1,00.
Exercício 6.12 A produtividade de feijão de lavouras de uma certa região produtora, segue uma distribuição normal de média 720,0 kg/ha e desvio padrão de 259,31 kg/ha. Encontre as seguintes probabilidades em %:
- Abaixo de 700,0 kg/ha;
- Acima de 760,0 kg/ha;
- Entre 650,0 e 680,0 kg/ha;
- Entre 750,0 e 800,0 kg/ha;
- Qual o valor de \(x\) que tem 80,0% de área acima dele.
Exercício 6.13 Num povoamento florestal os diâmetros à altura do peito (DAP), apresentam uma distribuição normal com média 18,2 cm e desvio padrão 3,4 cm.
- Foram cortados as 1.200 árvores que tinham DAP acima de 20,0 cm. Quantas árvores existiam no povoamento;
- Quantas árvores tem DAP menor que 16,0 cm;
- As árvores serão classificadas quanto ao seu DAP, nas seguintes categorias:
- Baixas – 30,0% menores;
- Médias – 40,0% intermediárias;
- Altas – as demais. Determine os limites para cada categoria.
- As árvores com DAP afastados da média em mais de 2 desvios padrão, serão avaliadas com cuidado, para se verificar a possibilidade de reconhecimento de genótipos inferiores ou superiores. Encontre a porcentagem de árvores que deverão ser avaliadas.
Exercício 6.14 Suponha que em uma lavoura a produtividade de grãos de milho, em ton/ha, seja uma variável aleatória X, tal que X \(\sim N(8,0; 1,69)\). Calcule as probabilidades:
- \(P(X \leq 4,0)\);
- \(P(X > 11,0)\);
- \(P(6,0 \leq X \leq 10,0)\);
- \(P(7,0 < X < 9,0)\);
- Qual o valor de \(x_c\) tal que \(P(X \leq x_{c})=0,90\).
Exercício 6.15 O peso dos frangos de uma granja se distribui segundo uma distribuição normal com média \(1,96\) kg e desvio padrão \(0,12\) kg. a) Num lote de 2.000 frangos quantos pesarão: - Menos de 2,0 kg; - Mais de 2,15 kg; - Exatamente 1,90 kg.
- Um abatedouro pretende comprar 5.000 frangos, classificando-os de acordo com o peso, da seguinte maneira:
- Categoria D – frangos pequenos – os 35,0% mais leves;
- Categoria C – frangos médios – os 30,0% seguintes;
- Categoria B – frangos grandes – os 25,0% seguintes;
- Categoria A – frangos extras – os 10,0% restantes. Quais serão os limites de peso de cada categoria, e quantos frangos terão em cada categoria.
- Os frangos com pesos superiores a 2,0 kg dão lucro de R$ 0,85 por cabeça; os com pesos entre 1,8 e 2,0 kg um lucro de R$ 0,37; e aqueles com pesos inferiores a 1,8 kg um prejuízo de R$ 0,25. Qual é o lucro médio por cabeça nesta granja.
Exercício 6.16 A variável aleatória Y: produção diária média de leite, num dado rebanho de vacas leiteiras do sul de Minas Gerais, pode ser considerada como sendo normalmente distribuída com média 19,0 kg e variância 14,44 \(\textrm{kg}^2\). a) Se um comprador deseja comprar apenas as vacas que produzam mais de 25,0 kg de leite, qual a porcentagem de vacas disponíveis para serem adquiridas; b) Se o preço das vacas variam de acordo com a tabela abaixo, qual o valor médio do rebanho.
| Produção \((Y)\) | Valor (R$) | |
|---|---|---|
| \(Y < 5,0\) kg | 800,00 | |
| \(5,0~\textrm{kg} \leq Y \leq 10,0~\textrm{kg}\) | 1.000,00 | |
| \(10,0~\textrm{kg} \leq Y \leq 20,0~\textrm{kg}\) | 1.900,00 | |
| \(20,0~\textrm{kg} \leq Y \leq 30,0~\textrm{kg}\) | 2.300,00 | |
| \(Y \geq 30,0~\textrm{kg}\) | 2.800,00 |
Exercício 6.17 Em uma procedência de eucalipto a probabilidade de que uma árvore seja resistente a uma praga é de 0,8. Um produtor plantou 625 árvores desta procedência. Determine a probabilidade de que haja mais de 514 árvores resistentes.
Exercício 6.18 Sabe-se que 8,0% dos tubos de irrigação produzidos por uma certa indústria apresentam defeito. Qual a probabilidade de que num lote com 300 tubos tomados ao acaso na linha de produção desta fábrica apresentam:
- 20 tubos defeituosos;
- De 22 à 27 tubos defeituosos;
- Menos de 19 tubos defeituosos;
- 31 ou mais tubos defeituosos.