3 Medidas de Posição
3.1 Introdução
No capítulo anterior vimos como organizar um conjunto de dados através de tabelas e gráficos, mas podemos ainda tirar mais informações importantes de um conjunto de dados através das medidas de posição. As medidas de posição, ou medidas de tendência central, são medidas representativas do valor central ao redor do qual se agrupam os dados, ou seja, procuram sintetizar um conjunto de dados em um único e informativo valor.
A média, a mediana e a moda são as três medidas de posição mais utilizadas para descrever um conjunto de dados, sejam eles populacionais ou amostrais.
3.2 Média
3.2.1 Dados Não Agrupados
A média de uma população ou amostra é dada pela soma de todos os dados da população ou amostra, dividida pelo número de dados que a compõem.
No caso dos dados provenientes de uma população, a média, denotada por \(\mu\), é dada pela expressão (3.1).
\[ \mu=\frac{\sum_{i=1}^{N}x_i}{N}. \tag{3.1}\]
E no caso dos dados provenientes de uma amostra, a média, denotada por \(\bar{x}\), é dada pela expressão (3.2).
\[ \bar{\text{x}}=\frac{\sum_{i=1}^{n}x_i}{n}. \tag{3.2}\]
A média funciona como um ponto de equilíbrio (de balanço), e é evidente que teremos dados acima e abaixo da média, mas todos os dados estarão na média, pois todos os dados fazem parte do cálculo da média.
A unidade da média será a mesma unidade dos dados.
Exemplo 3.1 Considere os dados do Exemplo 2.4. Neste caso trata-se de uma amostra. Assim, utilizando-se da expressão (3.2) tem-se que a média amostral é dada por:
\[\begin{align} \bar{\text{x}} & = \frac{21,0+21,6+22,1+...+31,3+31,8+33,0}{50} \Rightarrow \bar{\text{x}}=26,6~\textrm{kg}. \end{align}\]
3.2.2 Dados Agrupados
Se os dados estiverem agrupados em uma tabela de distribuição de frequências com intervalos de classes, a média é dada pela expressão (3.3). \[ \bar{\text{x}}=\frac{\sum_{i=1}^{K}F_{i}\tilde{X}_i}{\sum_{i=1}^{K}F_i}, \tag{3.3}\] em que: \(\tilde{X}_i\) é o ponto médio da classe \(i\) e \(F_i\) é a frequência absoluta da classe \(i\).
Exemplo 3.2 Considere o Exemplo 2.4. Alternativamente pode-se acrescentar mais uma coluna na tabela de distribuição de frequências referente a: \(F_{i}\tilde{X}_i\), que pode ser observado pela Tabela 3.1.
| Peso \(\mathbf{(kg)}\) | \(\mathbf{\tilde{X}_i}\) | \(\mathbf{F_i}\) | \(\mathbf{Fr_i}\) | \(\mathbf{Fp_i(\%)}\) | \(\mathbf{F_{i}\tilde{X}_i}\) |
|---|---|---|---|---|---|
| \(\left[20,0;22,0\right)\) | 21,0 | 2 | 0,04 | 4,0 | 42,0 |
| \(\left[22,0;24,0\right)\) | 23,0 | 5 | 0,10 | 10,0 | 115,0 |
| \(\left[24,0;26,0\right)\) | 25,0 | 12 | 0,24 | 24,0 | 300,0 |
| \(\left[26,0;28,0\right)\) | 27,0 | 16 | 0,32 | 32,0 | 432,0 |
| \(\left[28,0;30,0\right)\) | 29,0 | 10 | 0,20 | 20,0 | 290,0 |
| \(\left[30,0;32,0\right)\) | 31,0 | 4 | 0,08 | 8,0 | 124,0 |
| \(\left[32,0;34,0\right)\) | 33,0 | 1 | 0,02 | 2,0 | 33,0 |
| Total | 50 | 1,00 | 100,0 | 1.336,0 |
Logo, utilizando-se da expressão (3.3) tem-se que a média é dada por: \[ \bar{\text{x}}=\frac{1.336,0}{50}=26,7~\textrm{kg}. \]
Observa-se que a média para os dados não agrupados (26,6 kg) foi calculada usando os verdadeiros dados, e a média para os dados agrupados (26,7 kg) foi calculada usando os dados representados pelo ponto médio da classe \((\tilde{X}_i)\). Como se observa, a média calculada com os dados agrupados foi diferente da média para os dados não agrupados. No cálculo com os dados agrupados existe um erro devido à perda de informação, porém, tal erro é mínimo e, portanto, desprezível, o que mostra a qualidade do algoritmo utilizado para agrupar os dados numa Tabela de Distribuição de Frequências.
Neste caso o erro foi de: \[ Erro = 26,7 – 26,6 = 0,1~\textrm{kg}. \]
3.2.3 Propriedades
A média apresenta as seguintes propriedades:
- A soma dos desvios \((SD)\) de cada dado em relação à sua média é nula: \[ SD=\sum_{i=1}^{n}\left(x_i- \bar{\text{x}} \right)=0,0. \]
Exemplo 3.3 Seja uma amostra referente às alturas, em cm, de três plantas de uma variedade de milho, dada por: \[ 182,0; 184,0; 189,0. \]
Utilizando-se da expressão 3.2 a média é dada por:
\[ \bar{\text{x}}=\frac{182,0+184,0+189,0}{3}=\frac{555,0}{3}=185,0~\textrm{cm}. \]
Assim, a soma dos desvios de cada dado em relação à média é dada por: \[\begin{align} SD &= (182,0-185,0)+(184,0-185,0)+(189,0-185,0)\\ &= (-3,0)+(-1,0)+(4,0)=0,0. \end{align}\]
Que é um valor nulo comparado a qualquer outro valor diferente da média.
- A média é o valor que torna mínimo a soma de quadrados dos desvios \((SQD)\):
\[ SQD=\sum_{i=1}^{n}\left(x_i- \bar{\text{x}} \right)^2. \]
Exemplo 3.4 Considere o Exemplo 3.3, em que: \(\bar{x}=185,0\) cm.
Assim, tem-se que a soma de quadrados dos desvios \((SQD)\) é dada por: \[\begin{align*} SQD &= (182,0-185,0)^2+(184,0-185,0)^2+(189,0-185,0)^2\\ &= (-3,0)^2+(-1,0)^2+(4,0)^2=9+1+16=26,0. \end{align*}\] Que é um valor mínimo comparado a qualquer outro valor diferente da média.
- Somando-se ou subtraindo-se um mesmo valor constante \(k\) a cada dado, a média fica acrescida ou subtraída deste valor:
\[ x_i \pm k \Rightarrow \bar{\text{x}} \pm k. \]
Exemplo 3.5 Considere o Exemplo 3.3, em que: \(\bar{x}=185,0\) cm.
Somando-se \(k = 3,0\) cm a cada valor da amostra tem-se: \[ 185,0; 187,0; 192,0. \]
Utilizando-se da expressão (3.2) a nova média é dada por:
\[ \bar{\text{x}}=\frac{185,0+187,0+192,0}{3}=\frac{564,0}{3}=188,0~\textrm{cm}. \]
Ou seja, é a média anterior acrescida de \(3,0\) cm.
- Multiplicando-se ou dividindo-se cada dado por um mesmo valor constante \(k\), diferente de 0, a média fica multiplicada ou dividida por este valor:
\[ x_{i}\times k \Rightarrow \bar{\text{x}} \times k. \]
\[ \frac{x_i}{k} \Rightarrow \frac{\bar{\text{x}}}{k} \]
Exemplo 3.6 Considere o Exemplo 3.3, em que: \(\bar{\text{x}}=185,0\) cm. Multiplicando-se cada dado por \(k = 2\) tem-se:
\[ 364,0; 368,0; 378,0. \]
A nova média é dada por: \[ \bar{\text{x}}=\frac{364,0+368,0+378,0}{3}=370,0~\textrm{cm}. \] O que corresponde a média anterior multiplicada por 2.
3.3 Mediana
A mediana é o valor central de um conjunto dados, isto é, divide os dados ordenados ascendente ou descendentemente em partes iguais, ou seja, 50,0% dos dados estão acima e 50,0% estão abaixo deste valor. A mediana tem a mesma unidade dos dados.
3.3.1 Dados Não Agrupados
Neste caso os dados precisam primeiro serem ordenados de forma crescente ou decrescente.
A mediana no caso de uma amostra, sendo denotada por \(md\), é expressa da seguinte forma:
Se \(n\) for par a mediana é dada pela expressão (3.4). \[ md = \frac{x_{\left(\frac{n}{2}\right)}+x_{\left(\frac{n+2}{2}\right)}}{2}; \tag{3.4}\]
Se \(n\) for impar a mediana é dada pela expressão (3.5). \[ md=x_{\left(\frac{n+1}{2}\right)}. \tag{3.5}\]
Exemplo 3.7 Considere uma amostra referente às alturas, em cm, de sete plantas de uma variedade de milho, dada por: \[ 185,0; 182,0; 189,0; 182,0; 184,0; 188,0; 187,0. \] Para o cálculo da mediana os dados foram ordenados de forma crescente: \[ 182,0; 182,0; 184,0; 185,0; 187,0; 188,0; 189,0. \] Neste caso \(n\) = 7 (ímpar). Utilizando-se da expressão (3.5) tem-se que a mediana é dada por: \[ md=x_{\left(\frac{7+1}{2}\right)}=x_{(4)}, \] ou seja, corresponde ao 4º dado. Logo, a mediana é igual a \(185,0\) cm.
Exemplo 3.8 Seja uma amostra referente aos pesos, em kg, de oito leitões da raça Large White, dada por: \[ 38,2; 40,4; 38,5; 38,2; 37,4; 39,6; 40,1; 40,1. \]
Para o cálculo da mediana os dados foram ordenados de forma crescente: \[ 37,4; 38,2; 38,2; 38,5; 39,6; 40,1; 40,1; 40,4 \]
Tem-se que \(n\) = 8 (par). Utilizando-se da expressão (3.4) tem-se que a mediana é dada por: \[ md=\frac{x_{\left(\frac{8}{2}\right)}+x_{\left(\frac{8+2}{2}\right)}}{2}=\frac{x_{(4)}+x_{(5)}}{2}, \] ou seja, é a média entre o 4º e o 5º dado, dada por: \[ md=\frac{38,5+39,6}{2}=$39,05~\textrm{kg}. \]
Exemplo 3.9 Seja o Exemplo 2.4, e considerando os dados ordenados de forma crescente.
Neste caso tem-se que \(n\) = 50 (par). Utilizando-se da expressão (3.4) tem-se que a mediana é dada por: \[ md=\frac{x_{\left(\frac{50}{2}\right)}+x_{\left(\frac{50+2}{2}\right)}}{2}=\frac{x_{(25)}+x_{(26)}}{2}, \] ou seja, é a média entre o 25º e o 26º dado, dada por: \[ md=\frac{26,5+26,5}{2}=26,5~\textrm{kg}. \]
3.3.2 Dados Agrupados
Se os dados estiverem agrupados em uma Tabela de Distribuição de Frequências com intervalos de classes, a mediana é dada pela expressão (3.6),
\[ md=LI_{md}+\left[\frac{\frac{n}{2}-F_{A}}{F_{md}}\right]c_{md}, \tag{3.6}\] em que:
- \(LI_{md}\) é o limite inferior da classe mediana;
- \(F_A\) é a frequência acumulada anterior à classe mediana;
- \(F_{md}\) é a frequência absoluta da classe mediana;
- \(c_{md}\) é a amplitude da classe mediana.
A classe mediana é a classe que contém o dado: \(x_{\left(\frac{n}{2}\right)}\) (se \(n\) for par), ou \(x_{\left(\frac{n+1}{2}\right)}\) (se \(n\) for impar), na Tabela de Distribuição de Frequências.
Exemplo 3.10 Considere o Exemplo 2.4. A classe mediana é: \[ x_{\left(\frac{n}{2}\right)}=x_{\left(\frac{50}{2}\right)}=x_{(25)}=25º~\textrm{valor}. \]
Conta-se as freqüências absolutas até abranger o 25º valor. Neste caso tem-se: 2 + 5 + 12 + 16, ou seja, a 4ª classe, isto é, \([26,0; 28,0)\).
Assim, tem-se que:
- \(LI_{md}=26,0\) kg;
- \(F_A=2+5+12=19\);
- \(F_{md}=164\) ;
- \(c_{md}=2,0\) kg.
Utilizando-se da expressão (3.6) tem-se que a mediana é dada por:
\[ md=26,0+\left[\frac{\frac{50}{2}-19}{16}\right]2,0=26,75~\textrm{kg}. \] Tem-se que a diferença entre os dois valores (26,5 kg e 26,75 kg) se deve ao erro de agrupamento.
3.3.3 Propriedades
A mediana apresenta as seguintes propriedades:
- \(\sum_{i=1}^{n}|x_i-md|\) é um valor mínimo se comparado com qualquer outra expressão da forma: \(\sum_{i=1}^{n}|x_i-k|\) (sendo \(k\) um valor qualquer);
- Somando-se ou subtraindo-se um mesmo valor constante à cada dado, a mediana fica acrescida ou subtraída deste valor;
- Multiplicando-se ou dividindo-se cada dado por uma mesmo valor constante, diferente de 0, a mediana fica multiplicada ou dividida por este valor.
3.4 Moda
A moda de um conjunto de dados é o valor mais frequente, sendo denotada por \(mo\). Um conjunto de dados pode ter mais de uma moda, ou também, pode não ter moda. A moda tem a mesma unidade dos dados.
3.4.1 Dados Não Agrupados
Deve-se primeiro ordenar os dados de forma crescente ou decrescente, e em seguida contar o valor que ocorre mais vezes no conjunto de dados, ou seja, o valor mais frequente.
Exemplo 3.11 Considere uma amostra referente às alturas, em cm, de sete plantas de uma variedade de milho, dada por: \[ 185,0; 182,0; 189,0; 182,0; 184,0; 188,0; 187,0. \]
Para o cálculo da moda os dados foram ordenados de forma crescente: \[ 182,0; 182,0; 184,0; 185,0; 187,0; 188,0; 189,0, \] então, \[ mo=182,0~\textrm{cm (conjunto unimodal)}. \]
Exemplo 3.12 Seja uma amostra referente aos pesos, em kg, de oito leitões da raça Large White, dada por: \[ 38,2; 40,4; 38,5; 38,2; 37,4; 39,6; 40,1; 40,1. \]
Para o cálculo da moda os dados foram ordenados de forma crescente: \[ 37,4; 38,2; 38,2; 38,5; 39,6; 40,1; 40,1; 40,4. \] Portanto, \[ mo=38,2\textrm{e}~40,1~\textrm{kg (conjunto bimodal)}. \]
Exemplo 3.13 Seja uma amostra de cinco vacas leiteiras da raça holandesa, referentes a produção diária de leite, em kg,dada por: \[ 19,8; 18,2; 20,1; 20,9; 19,5. \] Para o cálculo da moda os dados foram ordenados de forma crescente: \[ 18,2; 19,5; 19,8; 20,1; 20,9. \] Neste caso a moda não existe (conjunto amodal).
Exemplo 3.14 Considere o Exemplo 2.4, e considerando os dados ordenados de forma crescente, tem-se que a moda é dada por: \[ mo = 27,2~\textrm{kg}. \]
Exemplo 3.15 Quando os dados estiverem agrupados em uma Tabela de Distribuição de Frequências com intervalos de classes, a moda se localiza na classe de maior frequência (classe modal), e é dada pela expressão (3.7), \[ mo=LI_{mo}+\left(\frac{\Delta_1}{\Delta_1+\Delta_2}\right) c_{mo}, \tag{3.7}\] em que:
- \(LI_{mo}\) é o limite inferior da classe modal;
- \(\Delta_1\) é a diferença entre a freqüência absoluta da classe modal e a classe anterior;
- \(\Delta_2\) é a diferença entre a freqüência absoluta da classe modal e a classe posterior;
- \(c_{mo}\) é a amplitude da classe modal.
Exemplo 3.16 Considerando o Exemplo 2.4, para o cálculo da moda tem-se:
- Classe Modal: [26,0 ; 28,0);
- \(LI_{mo}= 26,0\) kg;
- \(\Delta_1\)=16-12=4;
- \(\Delta_2\)=16-10=6;
- \(c_{mo}=2,0\) kg.
Utilizando-se da expressão (3.7) tem-se que a moda é dada por: \[ mo=26,0+\left(\frac{4}{4+6}\right) 2,0=26,8~\textrm{kg}. \]
A diferença entre os dois valores (\(27,2\) kg e \(26,8\) kg) se deve ao erro de agrupamento.
3.4.2 Propriedades
A moda apresenta as seguintes propriedades:
- Somando-se ou subtraindo-se uma mesmo valor constante a cada dado, a moda fica acrescida ou subtraída deste valor;
- Multiplicando-se ou dividindo-se cada dado por uma mesmo valor constante, diferente de 0, a moda fica multiplicada ou dividida por este valor.
A média, a mediana e a moda apresentam as seguintes vantagens e desvantagens.
- Vantagens:
- Média: tratável matematicamente;
- Mediana: não é influenciada por valores extremos;
- Moda: não é influenciada por valores extremos.
- Desvantagens:
- Média: é influenciada por valores extremos;
- Mediana: não é matematicamente tratável;
- Moda: não é matematicamente tratável.
3.5 Medidas de Posição e Natureza da Distribuição
A exemplo do polígono de frequências, a determinação das medidas de posição também permite discutir sobre a simetria da distribuição dos dados. E assim, conforme a Figura 3.1, pode-se observar a relação das medidas de posição com a natureza da distribuição.
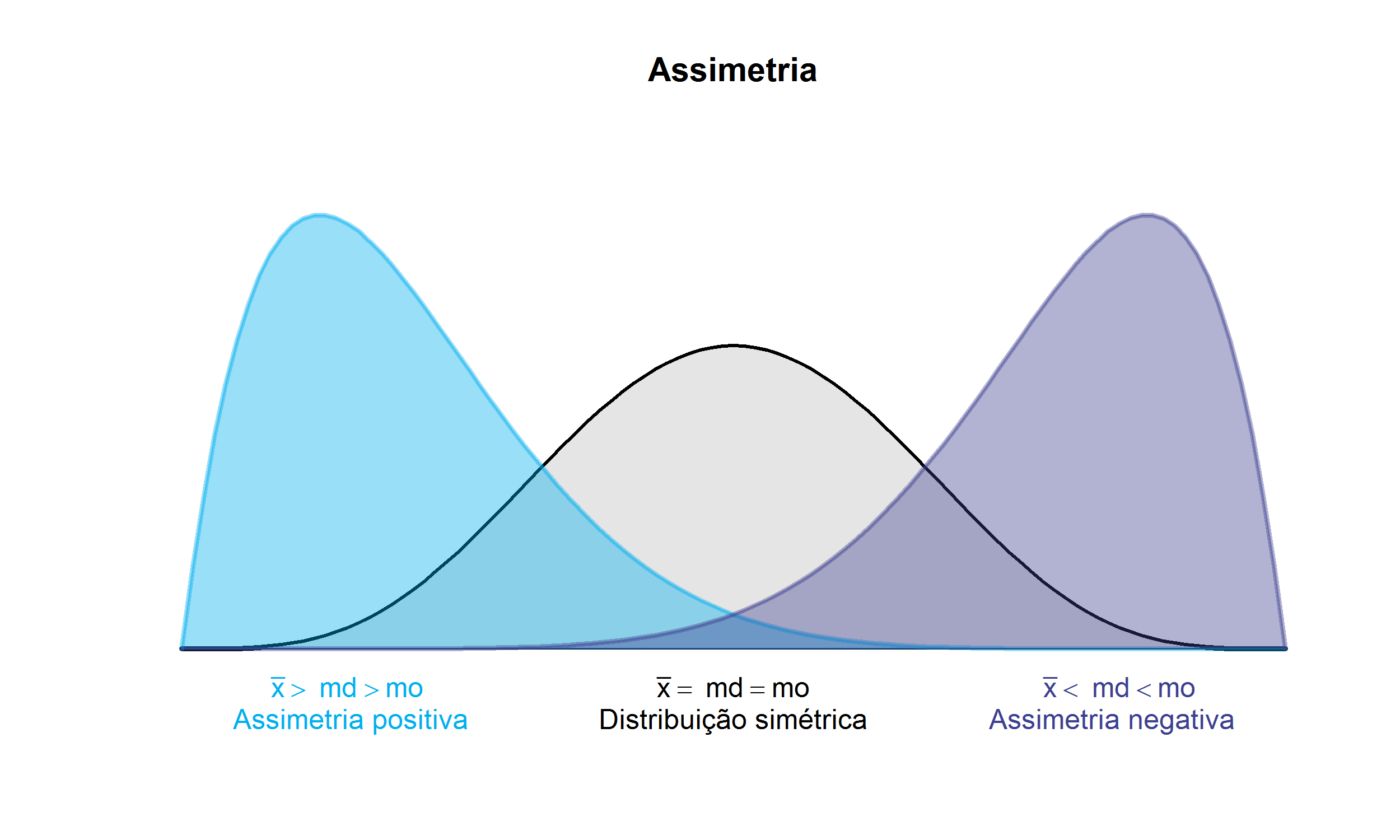
Exemplo 3.17 No Exemplo 2.4 tem-se:
- \(\bar{x}=26,70\) kg;
- \(md=26,75\) kg;
- \(mo=26,80\) kg.
Logo, a distribuição é simétrica.
3.6 Quantis
De um modo geral, pode-se definir uma medida, chamada quantil de ordem \(p\) ou \(p-quantil\), representada por \(q(p)\), sendo \(p\) uma proporção \((0,0 < p < 1,0)\), de tal forma que 100\(p\)% dos dados são menores do que \(q(p)\).
Os quantis mais empregados são:
- Quartis: Dividem os dados ordenados em ordem crescente em quatro partes iguais, sendo que: 25% dos dados serão inferiores ao primeiro quartil, 50% inferiores ao segundo quartil, que é a mediana, e 75% dos dados serão inferiores e 25% superiores ao terceiro quartil.
- Decis: Dividem os dados ordenados em ordem crescente em dez partes iguais.
- Percentis: Dividem os dados ordenados em ordem crescente em cem partes iguais.
Exemplo 3.18
- \(q(0,25): 1º\) Quartil = \(25º\) Percentil;
- \(q(0,50): 2º\) Quartil = Mediana = \(5º\) Decil = \(50º\) Percentil;
- \(q(0,75): 3º\) Quartil = \(75º\) Percentil;
- \(q(0,40): 4º\) Decil;
- \(q(0,95): 95º\) Percentil.
Segundo Bussab e Morettin (2010), o quantil de ordem \(p\) é definido pela expressão 3.8.
\[ q(p)=\begin{cases} x_{(i)} & \textrm{se } p = p_i, i=1,2,\ldots,n\\ (1-f_i)q(p_i)+f_iq(p_{i+1}) & \textrm{se } p_i<p<p_{i+1};\\ x_1 & \textrm{se } p<p_1;\\ X_n & \textrm{se } p>p_n, \end{cases} \tag{3.8}\] em que:
- \(p_{i}=\frac{i-0,5}{n}\);
- \(f_i=\frac{p-p_i}{p_{i+1}-p_i}\).
Exemplo 3.19 Considere o Exemplo 2.4, e usando a expressão 3.8. podem-se calcular, por exemplo, os seguintes quantis:
- \(q(0,1)\);
- \(q(0,2)\);
- \(q(0,5)\);
- \(q(0,75)\).
Assumindo: \[ p_{i}=\frac{i-0,5}{n}, \] então segue que:
- \(p_1=\frac{1-0,5}{50}=0,01\);
- \(p_2=\frac{2-0,5}{50}=0,03\);
- \(p_3=\frac{3-0,5}{50}=0,05\);
- \(p_4=\frac{4-0,5}{50}=0,07\);
- \(p_5=\frac{5-0,5}{50}=0,09\);
- \(p_6=\frac{6-0,5}{50}=0,11\);
- \(p_7=\frac{7-0,5}{50}=0,13\);
- \(p_8=\frac{8-0,5}{50}=0,15\);
- \(p_9=\frac{9-0,5}{50}=0,17\);
- \(p_{10}=\frac{10-0,5}{50}=0,19\);
- \(p_{11}=\frac{11-0,5}{50}=0,21\);
- \(p_{12}=\frac{12-0,5}{50}=0,23\);
- \(p_{13}=\frac{13-0,5}{50}=0,25\);
- \(\qquad\vdots\)
- \(p_{25}=\frac{25-0,5}{50}=0,49\);
- \(p_{26}=\frac{26-0,5}{50}=0,51\);
- \(\qquad\vdots\)
- \(p_{37}=\frac{37-0,5}{50}=0,73\);
- \(p_{38}=\frac{38-0,5}{50}=0,75\);
- \(p_{39}=\frac{39-0,5}{50}=0,77\);
- \(\qquad\vdots\)
- \(p_{49}=\frac{49-0,5}{50}=0,97\);
- \(p_{50}=\frac{50-0,5}{50}=0,99\).
- \(q(0,1)=?\) \[ p_5<0,1<p_6 \Rightarrow 0,09<0,1<0,11. \] \[ f_i=\frac{(p-p_i)}{(p_{i+1})-(p_i)}=\frac{0,1-0,09}{0,11-0,09}=0,5. \]
\[ q(p)=(1-f_i)q(p_i)+f_{i}q(p_{i+1}). \]
\[ q(0,1)=(1 – 0,5)q(p_5)+0,5q(p_6)=0,5(22,8) + 0,5(23,0)=$ 22,9~\textrm{kg}. \]
- \(q(0,2)=?\)
\[ p_{10}<0,2<p_{11} \Rightarrow 0,19<0,2<0,21. \]
\[ f_i=\frac{(p-p_i)}{(p_{i+1})-(p_i)}=\frac{0,2-0,19}{0,21-0,19}=0,5. \]
\[ q(p)=(1-f_i)q(p_i)+f_{i}q(p_{i+1}). \]
\[ q(0,2)=(1 – 0,5)q(p_{10})+0,5q(p_{11})=0,5(24,3) + 0,5(24,5)= 24,4~\textrm{kg}. \]
- \(q(0,5)=?\)
\[ p_{25}<0,5<p_{26} \Rightarrow 0,49<0,5<0,51. \]
\[ f_i=\frac{(p-p_i)}{(p_{i+1})-(p_i)}=\frac{0,5-0,49}{0,51-0,14}=0,5. \]
\[ q(p)=(1-f_i)q(p_i)+f_{i}q(p_{i+1}). \]
\[ q(0,5)=(1 – 0,5)q(p_{25})+0,5q(p_{26})=0,5(26,3) + 0,5(26,5)= 26,5~\textrm{kg}. \]
- \(q(0,75)=?\)
\[ q(0,75)=q(p_{38})=x_{38}=28,5~\textrm{kg}. \]
3.7 Esquema dos Cinco Números
O esquema dos cinco números são utilizados para se ter uma idéia da simetria da distribuição dos dados. A idéia é obter os cinco valores:
- \(x_1 \Rightarrow\) menor valor;
- \(q_1 \Rightarrow q(0,25)\);
- \(q_2 \Rightarrow q(0,50)\);
- \(q_3 \Rightarrow q(0,75)\);
- \(x_n \Rightarrow\) maior valor.
Para uma distribuição simétrica, ou aproximadamente simétrica, deve-se ter:
- \(q_2-x_1 \cong x_n - q_2\);
- \(q_2 - q_1 \cong q_3 - q_2\);
- \(q_1 - x_1 \cong x_n - q_3\);
- distâncias entre a mediana e \(q_1\), \(q_3\) menores do que distâncias entre os extremos e \(q_1\) e \(q_3\).
Exemplo 3.20 No exm-cont tem-se que:
- \(x_1=21,0\) kg;
- \(q_1=q(0,25)=24,9\) kg;
- \(q_2=q(0,50)=26,5\) kg;
- \(q_3=q(0,75)=28,5\) kg;
- \(x_n=33,0\) kg.
Pelos resultados conclui-se que a distribuição é aproximadamente simétrica.
Exercícios propostos
Exercício 3.1 Um Engenheiro Agrônomo interessado em estudar a produtividade de um canavial, demarcou nele em vários pontos escolhidos ao acaso, 10 pequenas áreas de 100 \(\textrm{m}^2\) cada, cuja produção foi pesada. Os resultados obtidos, em kg, foram os seguintes: \[ 650,0; 850,0; 710,0; 920,0; 780,0; 820,0; 900,0; 780,0; 740,0; 950,0. \]
Calcule a média, a mediana e a moda, da produção de cana-de-açúcar por área de 100 \(\textrm{m}^2\).
Exercício 3.2 Em relação ao estudo do problema anterior o Engenheiro Agrônomo achou que a variabilidade dos dados era muito grande, e que apenas 10 áreas de 100 \(\textrm{m}^2\) não representaram bem a produtividade do canavial. Assim ele avaliou no lugar de 10 uma amostra de 50 áreas de 100 \(\textrm{m}^2\), seguindo a mesma metodologia explicada no problema anterior. Os resultados obtidos, em kg, são apresentados na Tabela 3.2.
| Produção \(\mathbf{(kg)}\) | \(\mathbf{\tilde{X}_i}\) | \(\mathbf{F_i}\) |
|---|---|---|
| \(\left[624,0 \right. ;\left. 668,0 \right)\) | 646,0 | 1 |
| \(\left[668,0 \right. ;\left. 712,0 \right)\) | 690,0 | 5 |
| \(\left[712,0 \right. ;\left. 756,0 \right)\) | 734,0 | 15 |
| \(\left[756,0 \right. ;\left. 800,0 \right)\) | 778,0 | 13 |
| \(\left[800,0 \right. ;\left. 844,0 \right)\) | 822,0 | 7 |
| \(\left[844,0 \right. ;\left. 888,0 \right)\) | 866,0 | 5 |
| \(\left[888,0 \right. ;\left. 932,0 \right)\) | 910,0 | 3 |
| \(\left[932,0 \right. ;\left. 976,0 \right)\) | 954,0 | 1 |
| Total | 50 |
- Calcule a média, a mediana e a moda da produção de cana-de-açúcar por área de 100 \(\textrm{m}^2\);
- Após registrada a produção de cada uma das 50 áreas de 100 \(\textrm{m}^2\), o Engenheiro Agrônomo descobriu um erro sistemático na pesagem da cana-de-açúcar. Para obter a pesagem certa ele determinou que em cada um dos 50 dados obtidos deveria ser acrescido 6,0 kg, e depois o resultado deveria ser multiplicado por 0,9. Qual o valor correto da média, da mediana e da moda?
Exercício 3.3 Os pesos, em kg, de 6 novilhos nelore foram os seguintes: \[ 184,0; 193,0; 198,0; 204,0; 196,0; 207,0. \]
- Calcule a média dos pesos;
- Qual foi o desvio do \(2º\) animal em relação à média. Explique o que ele significa;
- Mostre que a soma dos desvios em relação à média é nula;
- Transforme os dados para arrobas. Calcule a média em arrobas partindo daquela obtida em (a);
- Adicione 20,0 kg em cada dado e encontre a média. Confronte o resultado com o obtido em (a). Qual a propriedade envolvida;
- Calcule a soma de quadrados dos desvios em relação à média e a 196,0. Discuta os resultados e tire conclusões.
Exercício 3.4 Um agricultor da região Sul de Goiás plantou três lavouras de milho, utilizando sementes de três diferentes empresas produtoras de sementes. Por amostragem ele avaliou a produtividade, em t/ha, de cada uma delas, no ano de 2006, obtendo os seguintes resultados:
| Empresa | Área plantada \(\mathbf{(ha)}\) | Produtividade \(\mathbf{(t/ha)}\) |
|---|---|---|
| 1 | 200,0 | 5,6 |
| 12 | 600,0 | 5,9 |
| 3 | 1.000,0 | 6,5 |
O agricultor solicitou a um Engenheiro Agrônomo que trabalha na região, para calcular a produtividade média de milho de sua propriedade. Após análise dos dados, o Engenheiro respondeu ao agricultor que sua produtividade média de milho foi de 6,0 t/ha. Você concorda ou não com a afirmativa do Engenheiro Agrônomo?
Exercício 3.5 Os ganhos de peso, em kg, de 60 novilhos da raça guzerá, mantidos numa pastagem em determinado período foram os seguintes:
| 36,0 | 45,0 | 60,0 | 39,0 | 57,0 | 32,0 | 39,0 | 40,0 | 63,0 | 37,0 |
| 42,0 | 42,0 | 44,0 | 30,0 | 47,0 | 39,0 | 15,0 | 39,0 | 25,0 | 39,0 |
| 57,0 | 48,0 | 44,0 | 37,0 | 44,0 | 38,0 | 21,0 | 56,0 | 52,0 | 50,0 |
| 31,0 | 34,0 | 36,0 | 38,0 | 43,0 | 24,0 | 38,0 | 41,0 | 46,0 | 42,0 |
| 28,0 | 31,0 | 32,0 | 49,0 | 39,0 | 19,0 | 49,0 | 39,0 | 42,0 | 43,0 |
| 20,0 | 58,0 | 34,0 | 56,0 | 35,0 | 50,0 | 27,0 | 36,0 | 40,0 | 37,0 |
- Calcule a média, a mediana e a moda do ganho de peso, em kg;
- Calcule os seguintes quantis:
- \(q(0,10)\);
- \(q(0,20)\);
- \(q(0,25)\);
- \(q(0,50)\);
- \(q(0,75)\);
- \(q(0,80)\).
- Determine o esquema dos cinco números e discuta sobre a simetria da distribuição dos dados.