5 Probabilidades – Estatística Básica aplicada às Ciências Agrárias

5.1 Introdução

Foi visto nos capítulos anteriores que a estatística descritiva nos auxilia a descrever uma amostra. Mas além de descrever a amostra, pode-se também estar interessado em saber se a informação contida na amostra, pode ser utilizada para inferir sobre as características da população da qual a amostra foi retirada. Porém, antes de estudar a inferência estatística, precisa-se conhecer alguns resultados importantes, pois a inferência estatística tem como base a teoria das probabilidades.

Neste capítulo são apresentados alguns fundamentos e teoremas, que serão utilizados como base teórica para o desenvolvimento de técnicas. a serem vistos em capítulos futuros.

5.2 Conceitos Básicos

Inicialmente são apresentados alguns conceitos que serão úteis no decorrer deste capítulo.

5.2.1 Experimento Determinístico

Um experimento determinístico é qualquer fenômeno ou ação que pode ser repetido, cujos resultados são sempre os mesmos, qualquer que seja o número de repetições.

Exemplo 5.1 Se a água for aquecida, ao atingir os 100°C de temperatura ela entrará em ebulição, independentemente do número de repetições.

5.2.2 Experimento Aleatório

Um experimento aleatório é qualquer fenômeno ou ação que pode ser repetido, cujos resultados são casuais ou aleatórios.

Exemplo 5.2 Seja um experimento que consiste em semear uma semente de feijão, e observar a sua germinação.

Exemplo 5.3 Considere um experimento em que se observa a vida útil de uma peça de um trator agrícola.

Exemplo 5.4 Imagine um experimento onde se observa o nascimento de três bezerros considerando a ordem, e determinar o sexo deles.

5.2.3 Espaço Amostral

O espaço amostral é o conjunto de todos os resultados possíveis de um experimento aleatório, cujos seus elementos são denominados eventos simples ou pontos amostrais. O espaço amostral é representado pela letra grega \(\Omega\).

Exemplo 5.5 Para o experimento do Exemplo 5.2, tem-se o espaço amostral associado ao experimento.

\[ \Omega=\left\{\textrm{germina},~ \textrm{não germina} \right\}. \]

Exemplo 5.6 Para o experimento do Exemplo 5.3, tem-se o espaço amostral associado ao experimento.

\[ \Omega=\left\{t \in \mathbb{R} | t \ge 0 \right\}, t = \textrm{tempo}. \]

Exemplo 5.7 Para o experimento do Exemplo 5.4, tem-se o espaço amostral associado ao experimento. \[\begin{align*} \Omega & = \left\{(M,M,M),~(M,M,F),~(M,F,M),~(F,M,M),~(M,F,F),~(F,M,F), \right. \\ & \quad \left. (F,F,M),~(F,F,F) \right\}. \end{align*}\] Sendo \(F\): fêmea e \(M\): macho.

5.2.4 Evento

Evento é um subconjunto do espaço amostral que representa um resultado definido. No estudo de probabilidades os eventos são representados por letras maiúsculas, tais como: A, B, C, etc.

Exemplo 5.8

Para o experimento do Exemplo 5.4, tem-se o seguinte evento de interesse: \(A\): Nascer exatamente duas fêmeas. Logo, tem-se que o evento A é formado pelo subconjunto de \(\Omega\) dado por: \(A = \left\{(M,F,F), (F,M,F), (F,F,M)\right\}\).

Então o evento A ocorre se ocorrer um dos três eventos simples: \((M,F,F)\) ou \((F,M,\) \(F)\) ou \((F,F,M)\).

5.3 Operações com Conjuntos (Eventos)

Sendo o espaço amostral um conjunto, e eventos um subconjunto do espaço amostral, muitos dos cálculos de probabilidades, que veremos nas próximas seções, envolvem operações com conjuntos. Assim, é interessante rever algumas operações com conjuntos dadas a seguir.

União ( \(\cup\) ): A união de dois eventos A e B \((A \cup B)\), é o evento que ocorre se pelo menos um deles ocorre. \(A \cup B = \left\{x|x \in A \textrm{ ou } x \in B \textrm{ ou ambos } \right\}\).
Interseção ( \(\cap\) ): A interseção de dois eventos A e B \((A \cap B)\) é definida como um conjunto com os elementos pertencentes simultaneamente aos eventos A e B. \(A \cap B = \left\{x|x \in A \textrm{ e } x \in B \right\}\).

Se dois eventos A e B têm interseção nula \((A \cap B = 0)\), diz-se que são mutuamente exclusivos ou disjuntos.

Evento Complementar (\(A^c\)): O evento complementar de A (\(A^c\)), é o evento que ocorre quando A não ocorre. \(A^{c} = \left\{x|x \notin A \right\}\).

Considerando A, B e C eventos, e com base nas operações definidas anteriormente, as seguintes relações são válidas:

\((A^c)^{c} = A\);
\(A \cup A^{c} = \Omega\);
\(\varnothing^{c} = \Omega\), sendo: \(\varnothing\) o conjunto vazio ou nulo;
\(A \cap A^{c} = \varnothing\);
\(\Omega^{c} = \varnothing\);
\(A \cup (B \cap C) = (A \cup B) \cap (A \cup C)\);
\(A \cap (B \cup C) = (A \cap B) \cup (A \cap C)\);
\(A \cap \varnothing = \varnothing\);
\(A \cup \varnothing = A\);
\((A \cap B)^{c} = A^{c} \cup B^{c}\);
\((A \cup B)^{c} = A^{c} \cap B^{c}\);
\(A \cap B = B \cap A\);
\(A \cup B = B \cup A\).

5.4 Métodos de Contagem

As ideias de contagem se relacionam com probabilidades, conforme será visto na próxima seção.

Arranjo: Considere escolher \(k\) dentre \(n\) objetos. Se a ordem de escolha é importante, tem-se um arranjo de \(n\) objetos tomados \(k\) a \(k\). O número de diferentes agrupamentos que podem ser formados é dado por: \(\text{A}_{n}^{k}=\frac{n!}{(n-k)!}\).
Combinação: Considere escolher \(k\) dentre \(n\) objetos. Se a ordem de escolha não importa, o agrupamento formado é a combinação de \(n\) objetos tomados \(k\) a \(k\). O número de diferentes agrupamentos que podem ser formados é dado por: \[ C^{k}_{n} = \frac{n!}{(n-k)!k!}. \]
Permutação: Um arranjo de \(n\) objetos tomados \(n\) a \(n\) é uma permutação de \(n\) objetos. O número de diferentes permutações é dado por: \[ P_{n}=n!. \]

5.5 Definição de Probabilidade

5.5.1 Definição Axiomática

Uma função \(P(~.~)\), com valores em [0,0; 1,0], é denominada probabilidade se satisfaz as seguintes condições:

A probabilidade de ocorrer um evento A é um valor não negativo. \[ P(A) \ge 0, \forall A \subset \Omega. \]
A probabilidade de ocorrer o espaço amostral \(\Omega\) é igual a 1. \[ P(\Omega) = 1. \]
Se \(B=\sum_{i=1}^{n}A_i\), sendo \(A_i, i = 1, 2, \ldots, n\), eventos mutuamente exclusivos, tem-se que:

\(P(B)=\sum_{i=1}^{n}P(A_i)\).

Essas condições são conhecidas como Axiomas de Kolmogorov.

5.5.2 Definição Clássica

Considere um espaço amostral \(\Omega\) associado a um experimento aleatório com \(n\) eventos simples, dado por: \[ \Omega=\left\{e_1,~e_2,~e_3,~\ldots,~e_n\right\}. \]

Supondo que os eventos simples de \(\Omega\) são igualmente prováveis de ocorrer (mesma chance), ou seja: \[ P(e_1)=P(e_2)=P(e_3)= \ldots=P(e_n)=\frac{1}{n}. \]

Considere agora um evento A de \(\Omega\) composto de \(m\) eventos simples. A probabilidade de ocorrer o evento A, representado por \(P(A)\), é definida por (5.1). \[ \begin{align} P(A)=\frac{m}{n}. \end{align} \tag{5.1}\]

Ou seja, a probabilidade de ocorrer o evento \(A\), é a razão entre o número de eventos simples do evento \(A\) (\(m\)), e o número de eventos simples de \(\Omega\) (\(n\)). Utilizando essa definição muitos problemas são resolvidos através de técnicas de análise combinatória.

Exemplo 5.9

Considerando o Exemplo 5.4 em que \(n\) = 8 eventos simples, e seja um evento A dado por: \(A\): Nascer exatamente duas fêmeas. Tem-se que o evento \(A\) é formado pelo subconjunto de \(\Omega\) dado por: \(A = \left\{(M,F,F), (F,M,F), (F,F,M)\right\} \Rightarrow m = 3\) eventos simples.

Assim, através de 5.1, a probabilidade de ocorrer o evento \(A\) é dada por: \[ P(A)=\frac{3}{8}=0,375=37,5\%. \]

Considere um evento \(B\) dado por: \(B\): Nascer pelo menos uma fêmea.

Tem-se que o evento \(B\) é formado pelo subconjunto de \(\Omega\) dado por: \[ \begin{align*} \textrm{B} & = \left\{(M,M,F),~(M,F,M),~(F,M,M),~(M,F,F),~(F,M,F), \right. \\ & \quad \left. (F,F,M),~(F,F,F) \right\} \Rightarrow m=7~\textrm{eventos simples}. \end{align*} \] Utilizando (5.1), tem-se que a probabilidade de ocorrer o evento \(B\) é dada por: \[ P(B)=\frac{7}{8}=0,875=87,5\%. \]

5.5.3 Definição Frequentista

Observa-se que em determinadas circunstâncias, pode-se atribuir a mesma chance a todos os eventos simples, associados ao experimento aleatório. Quando o número de eventos simples não for finito, essa possibilidade fica afastada. Outra maneira de determinar a probabilidade de um evento, consiste em repetir-se o experimento aleatório \(n\) vezes, e anotar quantas vezes um evento A associado a esse experimento ocorreu.

Seja \(n(A)\) o número de vezes em que um evento A ocorreu nas \(n\) tentativas (repetições) do experimento, então a razão dada por (5.2). \[ \begin{align} P(A)=\frac{n(A)}{n}, \end{align} \tag{5.2}\] é denominada frequência relativa de A nas \(n\) repetições do experimento.

Repetindo-se o experimento um grande número de vezes, nas mesmas condições, e de modo que as repetições sucessivas não dependam dos resultados anteriores, observa-se que a frequência relativa de ocorrências do evento A tende a uma constante \(p\), ou seja: \[\begin{align*} \lim_{n \to \infty} \frac{n(A)}{n} = p. \end{align*}\]

Exemplo 5.10 Considere um experimento, em que se semeou em uma área, 200 sementes de uma certa variedade de feijão, e após certo tempo, observou-se que 190 sementes germinaram.

Seja o evento A: \(A\): Número de sementes que germinam.

Através de 5.2, tem-se que a probabilidade de ocorrer o evento A é dada por: \[ P(A)=\frac{190}{200}=0,95=95,0\%. \]

5.6 Propriedades das Probabilidades

Em consequência da definição de probabilidade, tem-se as seguintes propriedades:

A probabilidade de um evento \(\varnothing\) é nula. \[ P(\varnothing)=0,0. \]
A probabilidade de ocorrer um evento A é um número entre 0,0 e 1,0. \[ 0,0 \leqslant P(A) \leqslant 1,0. \]
A probabilidade do evento complementar de A, definida por \(A^c\), é dada por: \[ P(A^{c})=1,0-P(A) \]
Se \(A \subset B \Rightarrow P(A) \leq P(B)\).
Para dois eventos A e B quaisquer, não mutuamente exclusivos, tem-se que: \[ P(A \cup B) = P(A) + P(B) - P(A \cap B). \]

5.7 Probabilidade Condicional

Frequentemente se tem o interesse no cálculo da probabilidade de que, um evento A ocorra dado que outro evento \(B\) também ocorra. Este tipo de probabilidade é chamado de probabilidade condicional, representada por \(P(A | B)\), que corresponde à probabilidade de ocorrência do evento A dado que ocorreu o evento \(B\), e é dada por (5.3). \[ \begin{align} P(A | B)=\frac{P(A \cap B)}{P(B)}, P(B) > 0. \end{align} \tag{5.3}\]

Tem-se que a probabilidade de B dado A é expressa por (5.4). \[ \begin{align} P(B | A)=\frac{P(A \cap B)}{P(A)}, P(A) > 0. \end{align} \tag{5.4}\]

Além de servirem como modelagem para situações práticas, probabilidades condicionais podem auxiliar no cálculo de probabilidades em geral.

Exemplo 5.11 Considere uma máquina de encher sacos com farelo de trigo, e os seguintes eventos: \[\begin{align*} \textrm{A}: & \textrm{ A máquina ultrapassa o limite máximo de enchimeno;}\\ \textrm{B}: & \textrm{ Os sacos apresentam algum defeito.} \end{align*}\]

Sejam as seguintes probabilidades:

\(P(A)=0,05\);
\(P(B)=0,10\).

Considere que a probabilidade de que um saco ultrapasse o limite máximo de enchimento, e que apresente algum defeito, seja 1,0%, ou seja, \(P(A \cap B)=0,01\).

A probabilidade da máquina ultrapassar o limite máximo de enchimento, dado que o saco vem com algum defeito é dada por: \[ P(A | B)=\frac{P(A \cap B)}{P(B)}=\frac{0,01}{0,10}=0,1=10,0\%. \]

Definida probabilidade condicional, pode-se deduzir a regra do produto de probabilidades.

Sejam A e B dois eventos associados ao espaço amostral \(\Omega\). Tem-se que: \[ \begin{align} P(A \cap B)=P(A | B)P(B)=P(B | A)P(A). \end{align} \tag{5.5}\]

A partir de (5.5), pode-se obter a probabilidade de ocorrer o evento B da seguinte forma: \[ \begin{align} P(B)=P(A \cap B)+P(A^c \cap B)=P(B | A)P(A)+P(B | A^c)P(A^c) \end{align} \tag{5.6}\]

A expressão (5.6) é conhecida como regra da probabilidade total.

5.8 Teorema de Bayes

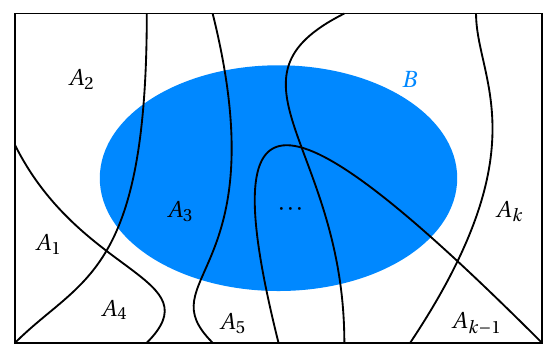
Seja um espaço amostral \(\Omega\), o qual é subdividido nos eventos \(A_1\), \(A_2\), \(A_3\), \(\ldots\), \(A_k\), mutuamente exclusivos, com probabilidades conhecidas. Considere um evento \(B\) contido nesse espaço, conforme figura abaixo. Suponha que as probabilidades \(P(B | A_i), i = 1, 2, \ldots, k\), sejam conhecidas.

A probabilidade de ocorrência do evento \(A_i\) dado a ocorrência do evento \(B\), é dada por (5.7). \[ \begin{align} P(A_i | B)=\frac{P(B | A_i)P(A_i)}{\sum_{i=1}^{k}P(B | A_i) P(A_i)}, i=1, 2, \ldots, k. \end{align} \tag{5.7}\]

Essa relação é conhecida como “Teorema de Bayes”, usada no cálculo de probabilidades condicionais.

Figura 5.1: Representação do teorema de Bayes pelo diagrama de Venn.

Exemplo 5.12 Suponha que uma agroindústria recebe: 20,0% de todo o leite que utiliza proveniente de uma Fazenda \(F_1\), 30,0% de uma outra Fazenda \(F_2\), e 50,0% da Fazenda \(F_3\). O Órgão responsável pela fiscalização sanitária da região, inspecionou as três fazendas de surpresa. Os fiscais observaram que: 20,0% do leite produzido pela Fazenda \(F_1\) estava adulterado pela adição de água, e nas Fazendas \(F_2\) e \(F_3\) a proporção era de 5,0% e 2,0%, respectivamente. Na agroindústria os latões de leite são armazenados em um refrigerador, sem identificação de procedência. Um latão é escolhido ao acaso, e é feita a análise do leite, para decidir sobre sua adulteração ou não. Qual é a probabilidade da amostra adulterada (\(A\)), ter sido proveniente do leite produzido pela Fazenda \(F_1\).

Assim, tem-se as seguintes probabilidades:

\(P(F_{1}) = 0,20\);
\(P(F_{2}) = 0,30\);
\(P(F_{3}) = 0,50\);
\(P(A | F_{1}) = 0,20\);
\(P(A | F_{2}) = 0,05\);
\(P(A | F_{3}) = 0,02\).

A probabilidade desejada é dada por: \[\begin{align*} P(F_1 | A) &= \frac{P(A | F_1)P(F_1)}{P(A | F_1)P(F_1)+P(A | F_2) P(F_2)+P(A | F_3)P(F_3)}\\ &= \frac{0,20(0,20)}{0,20(0,20)+0,05(0,30)+0,02(0,50)}\\ &=0,615=61,5\% \end{align*}\]

Logo, a probabilidade de que a amostra de leite tenha sido proveniente da Fazenda \(F_1\) é de 61,5%.

5.9 Eventos Independentes

Dois eventos A e B são independentes se, a probabildade de ocorrência de um deles não afeta a probabilidade de ocorrência do outro. Assim, dois eventos A e B são independentes se, qualquer uma das seguintes afirmações abaixo for verdadeira:

\(P(A | B) = P(A)\);
\(P(B | A) = P(B)\);
\(P(A \cap B) = P(A)P(B)\).

Se dois eventos A e B são independentes, então tem-se que: \[ P(A \cup B) = P(A) + P(B) - P(A) P(B). \]

5.10 Variável Aleatória

Considere, por exemplo, um experimento que consiste em semear em um canteiro, três sementes de uma variedade de feijão, e observar a sua germinação.

Assim, o espaço amostral é dado por: \[\begin{align*} \Omega & = \left\{(G,G,G),~(G,G,N),~(G,N,G),~(G,N,N),~(N,G,G),~(N,G,N), \right. \\ & \quad \left. (N,N,G),~(N,N,N) \right\} \Rightarrow n=8 ~ \textrm{eventos simples}, \end{align*}\] sendo \(G\): Germina e \(N\): Não germina.

Se o experimento fosse semear oito sementes, o espaço amostral teria: \(2^8=256\) eventos simples,

o que seria bastante trabalhoso de ser construído.

Logo, para tornar o fenômeno matematicamente simples, costuma-se associar por meio de uma função, números a cada um dos eventos simples do espaço amostral, criando assim um novo conjunto.

Para o exemplo anterior, poderia-se, por exemplo, através de uma variável (\(X\)) previamente definida, especificar o número de sementes que germinam. Assim, tem-se: \(X\): Número de sementes que germinam.

A Tabela 5.1 apresenta os eventos simples de \(\mathbf{\Omega}\), e os valores que a variável X pode assumir.

Tabela 5.1: Eventos simples de \(\Omega\) e valores de \(X\).

Eventos simples de \(\mathbf{\Omega}\)	Valores de \(\mathbf{X}\)
\((G,G,G)\)	3
\((G,G,N)\)	2
\((G,N,G)\)	2
\((G,N,N)\)	1
\((N,G,G)\)	2
\((N,G,N)\)	1
\((N,N,G)\)	1
\((N,N,N)\)	0

Logo, tem-se que o conjunto dos possíveis valores que a variável \(X\) pode assumir é: \(\left\{0, 1, 2, 3\right\}\).

Assim, mediante uma variável previamente definida, associa-se um número a cada evento simples do espaço amostral, e em lugar de calcular a probabilidade de ocorrência do evento, calcula-se a probabilidade de ocorrência desse número.

Logo, uma variável aleatória é uma função que associa a cada evento simples do espaço amostral um número real. Como cada evento aleatório está relacionado com uma probabilidade de ocorrência, então, cada um dos possíveis valores da variável aleatória estará também relacionado com uma probabilidade de ocorrência.

A variável aleatória é representada por letras maiúsculas, por exemplo, \(X\), \(Y\), \(Z\), etc, e os valores que a variável podem assumir por letras minúsculas, por exemplo, \(x\), \(y\), \(z\), etc.

As variáveis aleatórias podem ser classificadas em:

Discretas: Quando assumem somente um número finito ou enumerável de resultados.

Exemplo 5.13

Número de ervas daninhas num canteiro;
Número de frutos de uma árvore frutífera;
Número de plantas sadias numa amostra de cinco plantas;
Número de bezerras num rebanho de gado holandês;
etc.

Contínuas: Quando assumem qualquer valor dentro de um intervalo especificado ou contínuo.

Exemplo 5.14

Consumo de ração dos suínos de uma granja;
Altura das plantas de milho de uma lavoura;
Produção das plantas de feijão numa parcela;
Peso de frangos de uma granja;
Produção de leite de um rebanho leiteiro;
etc.

5.11 Função de Probabilidade Discreta

É uma função, representada por \(P(X = x)\), que associa cada valor x que a variável aleatória discreta X pode assumir, a sua respectiva probabilidade, a qual deve satisfazer as seguintes condições:

\(0 \leq P(X = x) \leq 1\);
\(\sum_{i=1}^{n}P(X = x_i) = 1\).

Exemplo 5.15 Seja uma variedade de café, em que 85,0% das plantas são resistentes à broca do cafeeiro. Logo, uma planta desta variedade pode ser: \[\begin{align*} \begin{cases} \textrm{Resistente } (R) & \Rightarrow P(R) = 85,0\% = 0,85;\\ \textrm{Não-Resistente } (N) & \Rightarrow P(N) = 15,0\% = 0,15. \end{cases} \end{align*}\]

Duas plantas são selecionadas desta variedade de café, cujo espaço amostral é dado por: \[ \Omega=\left\{(R,R), (R,N), (N,R), (N,N)\right\}. \]

Definindo a variável aleatória X como: \(X\): Número de plantas resistentes à broca do cafeeiro.

Os possíveis valores para X são: \(\{0, 1, 2\}\).

Considerando a independência entre os eventos, tem-se que as probabilidades dos eventos simples do espaço amostral \(\Omega\) são dadas por:

Valores de \(\mathbf{X}\)	Eventos simples de \(\mathbf{\Omega}\)	Probabilidades
0	\((N,N)\)	0,15(0,15) = 0,0225
1	\((R,N)\), \((N, R)\)	0,85(0,15) + 0,15(0,85) = 0,255
2	\((R,R)\)	0,85(0,85) = 0,7225

Dessa forma, pode-se construir uma tabela, chamada de distribuição de probabilidades da variável aleatória X, apresentada na Tabela 5.2.`

Tabela 5.2: Distribuição de probabilidade da variável aleatória X.

\(\mathbf{x}\)	\(\mathbf{P(X = x)}\)
0	0,0225
1	0,2550
2	0,7225

Que também pode ser apresentada da seguinte forma:

\(\mathbf{x}\)	0	1	2
\(\mathbf{P(X = x)}\)	0,0225	0,2550	0,7225

A partir da tabela acima, pode-se verificar as duas condições necessárias para que \(P(X = x)\) seja uma função de probabilidade discreta legítima, da seguinte forma:

\(0,0 \leq P(X = x) \leq 1,0\): \[\begin{align*} P(X = x) = \begin{cases} 0,0 & x < 0;\\ 1,0 & 0 \leq x \leq 2;\\ 0,0 & x > 2. \end{cases} \end{align*}\]
\(\sum_{i=1}^{n}P(X = x_i) = 0,0225 + 0,2550 + 0,7225 = 1,0\).

Satisfeitas as duas condições, tem-se que \(P(X = x)\), é uma função de probabilidade discreta legítima.

Note que a Tabela 5.2 se parece com as tabelas de distribuições de frequências vistas no Capítulo 2. Foi visto que as distribuições de frequências inclui também a frequência relativa de cada classe. No caso de variáveis aleatórias, as probabilidades representam a frequência relativa de ocorrência de cada resultado \(x\), em um grande número de experimentos repetidos sob as mesmas condições, ou equivalentemente, elas podem ser interpretadas como sendo as frequências relativas, associadas com amostras infinitamente grandes.

As probabilidades nos permitem observar, quais valores da variável aleatória são mais prováveis de ocorrer dentro de uma experiência.

A distribuição de probabilidades da variável aleatória X (número de plantas resistentes à broca do cafeeiro), pode ser usada para se fazer algumas afirmações a respeito dos possíveis resultados da variável aleatória. Por exemplo, a probabilidade de uma planta escolhida aleatoriamente ser resistente é de 0,2550 ou 25,50%. Pode-se também ter o interesse em saber qual a probabilidade de uma ou duas plantas desta variedade de café, serem resistentes à broca do cafeeiro. Assim, como são dois eventos mutuamente exclusivos, tem-se que a probabilidade de ocorrência de uma ou duas plantas resistentes, é igual a soma de suas probabilidades individuais, ou seja: \[\begin{align*} \sum_{x = 1}^{2}P(X = x) & = P(X = 1) + P(X = 2)\\ & = 0,2550 + 0,7225\\ & = 0,9775 = 97,75\% \end{align*}\]

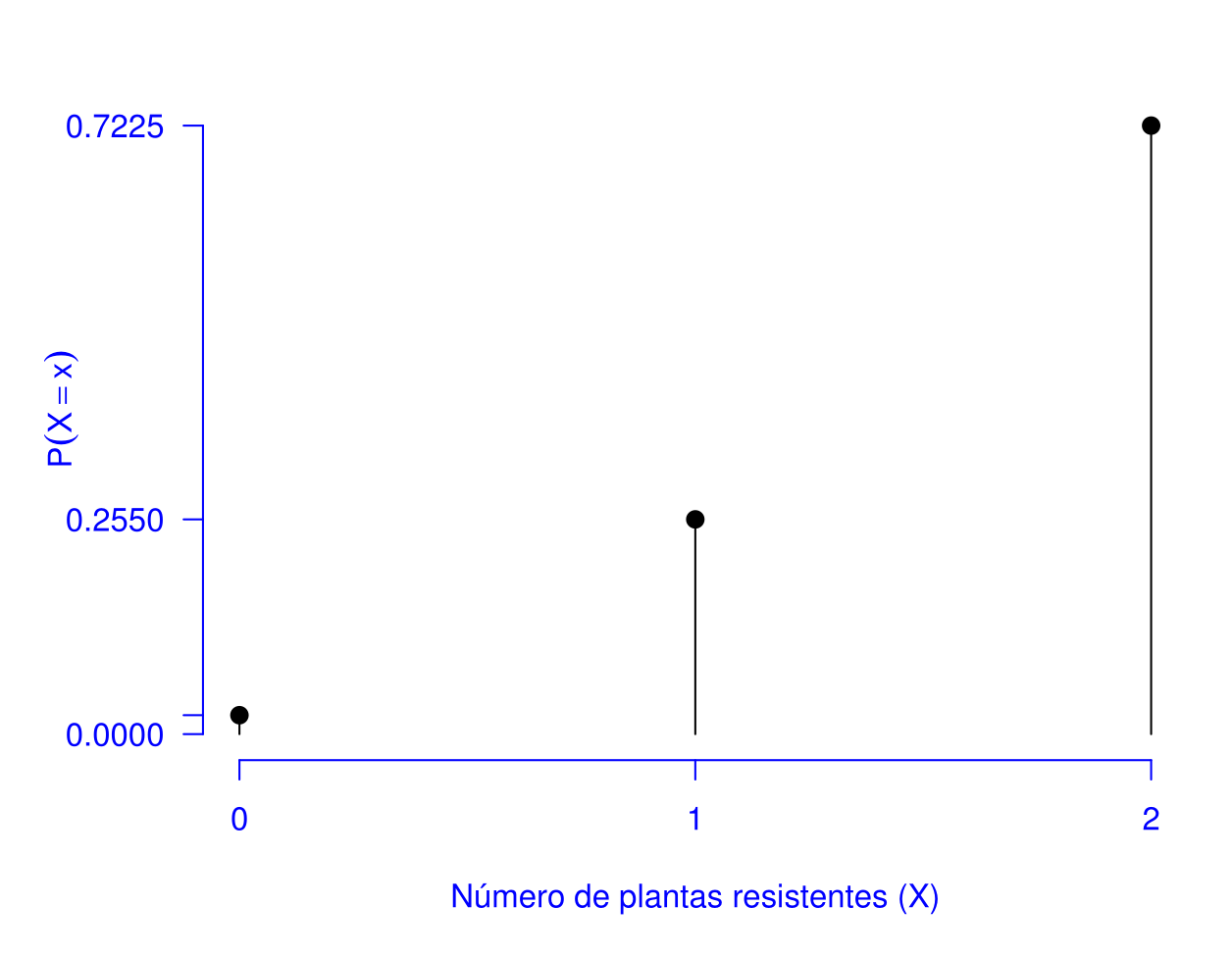
A distribuição de probabilidades da variável aleatória X pode ser representada graficamente através da Figura 5.2.

Figura 5.2: Distribuição de probabilidades para a variável aleatória discreta X (número de plantas resistentes

5.12 Função Densidade de Probabilidade

Se a variável aleatória é contínua, calcula-se a probabilidade por meio da integração da área abaixo da função densidade de probabilidade \((f.d.p.)\).

Uma função \(f(x)\) é uma função densidade de probabilidade, se satisfaz as seguintes condições:

\(f(x) \geq 0,0, \forall x \in \mathbb{R}\);
\(\int_{-\infty}^{\infty} f(x) \, dx=1,0\).

5.12.1 Propriedades da Função Densidade de Probabilidade

A função densidade de probabilidade apresenta as seguintes propriedades:

\(P(a \leq X \leq b)=P(a < X \leq b)=P(a \leq X < b)=P(a < X < b)=\int_{a}^{b} f(x) \, dx\), para quaisquer \(a\) e \(b\), sendo \(a < b\);
\(P(X = k)=0\), sendo \(k\) uma constante, ou seja, a probabilidade da variável aleatória assumir um valor específico é nula, pois \(\int_{k}^{k} f(x) \, dx=0\).

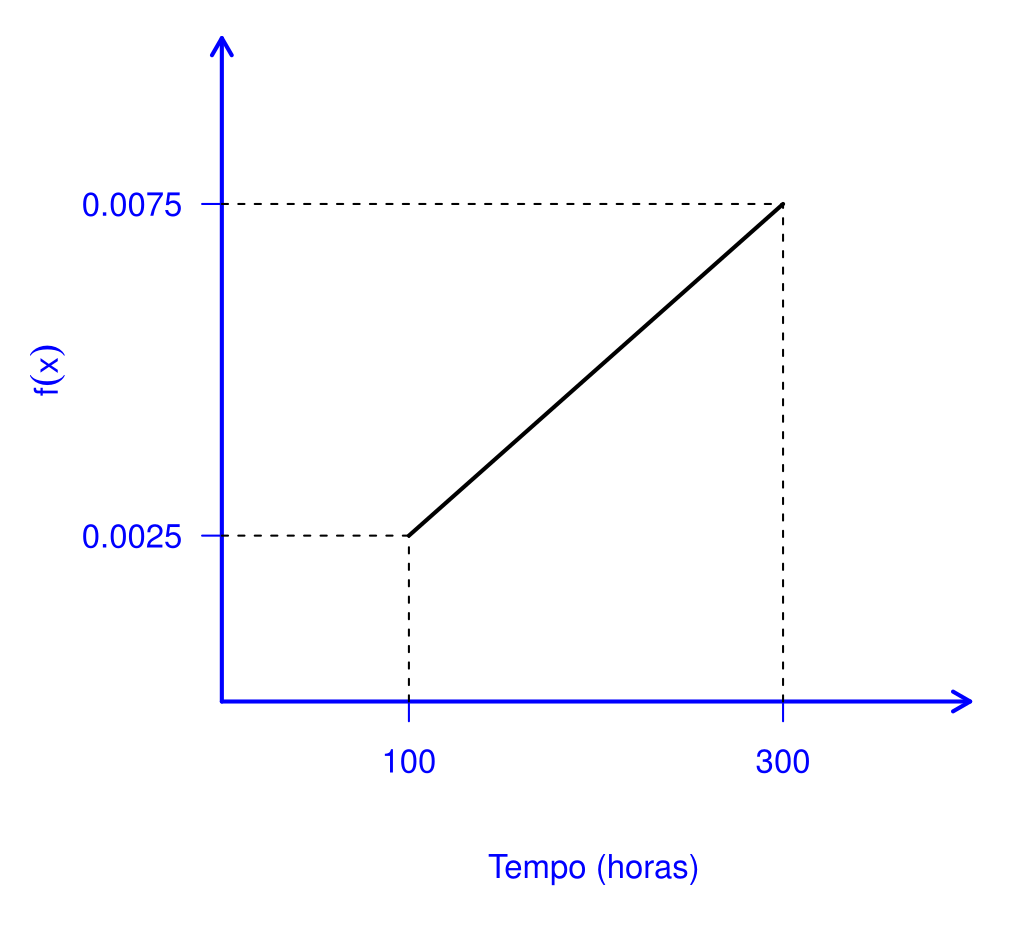
Exemplo 5.16 O tempo de duração de embreagens em tratores agrícolas de certa marca, sujeitos a uso contínuo, pode ser considerado como uma variável aleatória contínua, medido em horas, cuja função densidade de probabilidade é dada por: \[\begin{align*} f(x)=\begin{cases} \frac{x}{40.000} & \textrm{para } 100 \leq x \leq 300;\\ 0,0 & \textrm {caso contrário.} \end{cases} \end{align*}\]

Tem-se que \(f(x)\) pode ser representado graficamente através da Figura 5.3.

Neste caso a variável aleatória X é definida por: \(X\): Tempo de duração, em horas, de embreagens em tratores agrícolas.

Para verificar se \(f(x)\) é uma função densidade de probabilidade legítima, tem-se que satisfazer as duas condições necessárias vistas acima.

Logo, tem-se:

\(f(x) \geq 0,0, \forall x \in \mathbb{R}\): \[\begin{align*} \left\{ \begin{array}{ll} \textrm{Para } x < 100 & \Rightarrow f(x)=0,0;\\ \textrm{Para } 100 \leq x \leq 300 & \Rightarrow f(x) > 0,0;\\ \textrm{Para } x > 300 & \Rightarrow f(x)=0,0. \end{array}\right. \end{align*}\]
\(\int_{-\infty}^{\infty} f(x) \, dx=1,0\): \[\begin{align*} \int_{100}^{300} \frac{x}{40.000}dx & =\frac{1}{40.000}\int_{100}^{300} xdx\\ & = \left. \left(\frac{1}{40.000}\times \frac{x^2}{2} \right)\right|_{100}^{300} \\ & =\frac{90.000-10.000}{80.000}=1,0. \end{align*}\]

Satisfeitas as duas condições, tem-se que \(f(x)\) é uma função densidade de probabilidade.

Assim, pode-se calcular, por exemplo, a probabilidade do tempo de duração estar entre 200 e 300 horas, dada por: \[\begin{align*} P(200 < X < 300) &= \int_{200}^{300} \frac{x}{40.000}dx\\ &= \frac{1}{40.000}\int_{200}^{300} xdx\\ &= \left( \frac{1}{40.000}\times \frac{x^2}{2} \right)\Big|_{200}^{300}\\ & =\frac{90.000-40.000}{80.000}\\ &= \frac{50.000}{80.000}\\ &= 0,625 = 62,5\%. \end{align*}\]

5.13 Função de Distribuição Acumulada

A função de distribuição acumulada de uma variável aleatória, discreta ou contínua, é definida como sendo a probabilidade de que a variável esteja abaixo de um determinado valor, ou seja: \[ \begin{align} F(x)=P(X\leq x), \quad \forall x \in \mathbb{R}. \end{align} \tag{5.8}\]

5.13.1 Variável Aleatória Discreta

Para uma variável aleatória discreta, a função de distribuição de probabilidade acumulada é dada por: \[ \begin{align} F(x)=\sum_{x_i \leq x}P(X = x_i), \quad x \in \mathbb{R}. \end{align} \tag{5.9}\]

Exemplo 5.17 Considerando a variável aleatória discreta X, que representa o número de lesões nas folhas de plantas de café provocadas por uma praga, cujos possíveis valores são: \(\{0, 1, 2, 3, 4, 5\}\).

A distribuição de probabilidade de \(X\) é dada por:

\(\mathbf{x}\)	0	1	2	3	4	5
\(\mathbf{P(X = x)}\)	0,32	0,28	0,20	0,12	0,06	0,02

Por exemplo, a probabilidade de 3 lesões ou menos, é dada por: \[\begin{align*} F(3) & = P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)\\ & = 0,32 + 0,28 + 0,20 + 0,12\\ & = 0,92 = 92\%. \end{align*}\]

De uma maneira geral, tem-se a seguinte função de distribuição de probabilidade acumulada para a variável aleatória X, definida acima: \[\begin{align*} F(x)=\begin{cases} 0,0 & \textrm{se }x < 0;\\ 0,32 & \textrm{para }0 \leq x < 1;\\ 0,60 & \textrm{para }1 \leq x < 2;\\ 0,80 & \textrm{para }2 \leq x < 3;\\ 0,92 & \textrm{para }3 \leq x < 4;\\ 0,98 & \textrm{para }4 \leq x < 5;\\ 1,0 & \textrm{se }x \geq 5. \end{cases} \end{align*}\]

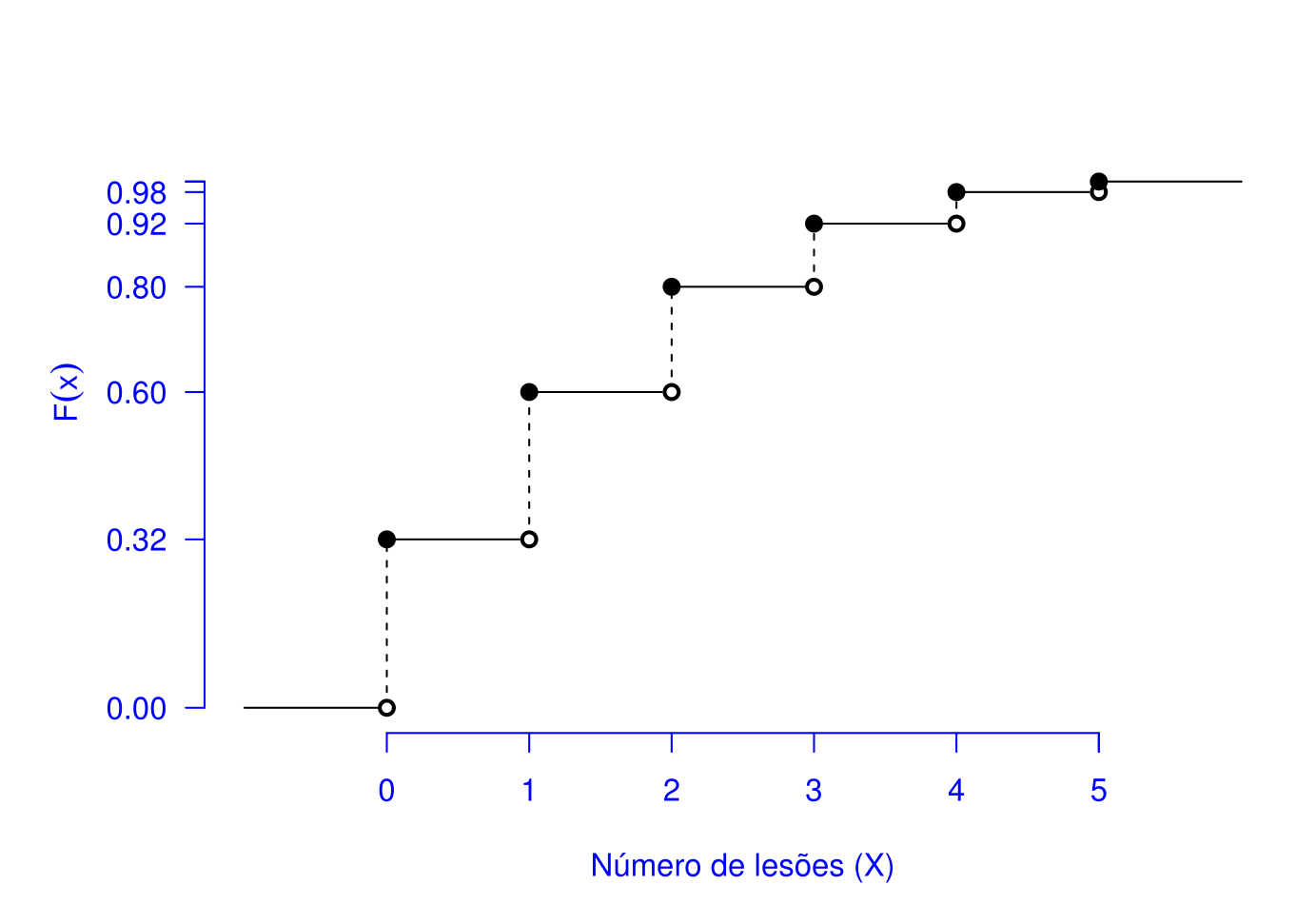
A função \(F(x)\) pode ser disposta graficamente. Sendo a variável aleatória discreta, a representação é por meio de um gráfico de escadas.

Exemplo 5.24 Para o Exemplo 5.17 tem-se:

Figura 5.4: Função de distribuição acumulada para o número de lesões nas folhas do cafeeiro.

5.13.2 Variável Aleatória Contínua

Se a variável aleatória for contínua, a função de distribuição de probabilidade acumulada é dada por: \[ F(x)=\int_{-\infty}^{x} f(t)dt. \]

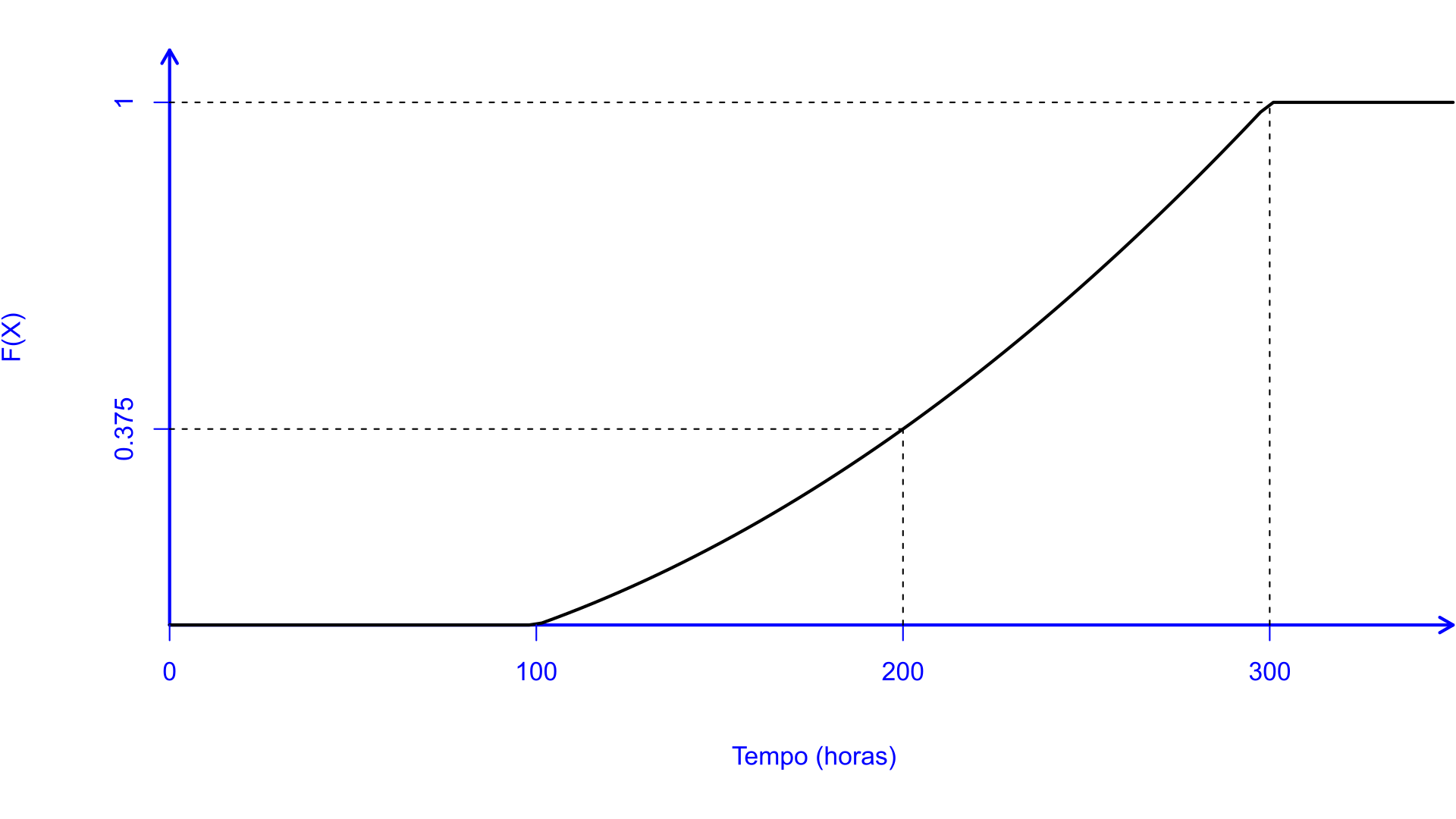
Exemplo 5.18 Considerando o Exemplo 5.16, tem-se que sua função de distribuição de probabilidade acumulada é obtida por: \[\begin{align*} F(x) & =\int_{100}^{x} \frac{t}{40.000}dt\\ & = \frac{1}{40.000}\int_{100}^{x} t dt\\ & = \left. \left(\frac{1}{40.000}\times \frac{t^2}{2}\right) \right|_{100}^{x} \\ & =\frac{x^2-10.000}{80.000}. \end{align*}\]

Assim, por exemplo, a probabilidade de que a embreagem dure 200 horas ou menos é dada por: \[\begin{align*} F(200) &= \frac{200^2-10.000}{80.000}\\ &= \frac{40.000-10.000}{80.000}\\ &= \frac{30.000}{80.000}\\ &= 0,375=37,5\%. \end{align*}\]

A função \(F(x)\) pode ser disposta graficamente. Para variáveis aleatórias contínuas tem-se uma função \(F(x)\) contínua.

Exemplo 5.19 Para o Exemplo 5.18, tem-se:

Figura 5.5: Função de distribuição acumulada para o tempo de duração de embreagens em tratores agrícolas.

5.13.3 Relações da Função de Distribuição Acumulada

De uma maneira geral tem-se as seguintes relações envolvendo \(F(x)\):

\(0 \leq F(x) \leq 1\);
Se \(x_1 < x_2 \Rightarrow F(x_1) \leq F(x_2)\);
\(\displaystyle\lim_{n \to -\infty} F(x) = 0,0\);
\(\displaystyle\lim_{n \to \infty} F(x) = 1,0\).

5.14 Medidas de Posição e Dispersão para Variáveis Aleatórias

Às vezes uma variável aleatória, discreta ou contínua, pode assumir um grande número de valores. Tal como vimos para a distribuição de frequências, podemos resumir uma distribuição de probabilidades, através de uma medida de posição e uma medida de dispersão.

5.14.1 Esperança Matemática

O valor médio assumido pela variável aleatória, é conhecido como média da distribuição, também chamado de esperança matemática.

A esperança matemática é um valor esperado, não sendo necessariamente um resultado da experiência.

5.14.1.1 Variável Aleatória Discreta

A esperança matemática de uma variável aleatória discreta, é dada pela expressão (5.10). \[ \begin{align} E(X)=\mu=\sum_{i=1}^{\infty} x_iP(X = x_i). \end{align} \tag{5.10}\]

Exemplo 5.20 Para o Exemplo 5.17, e utilizando-se da expressão (5.10), tem-se:

\[\begin{align*} E(X)=\mu & = 0(0,32) + 1(0,28) + 2(0,20) + \\ & \quad + 3(0,12) + 4(0,06) + 5(0,02)\\ & = \mu=1,38~\textrm{lesões}. \end{align*}\]

5.14.1.2 Variável Aleatória Contínua

A esperança matemática de uma variável aleatória contínua, é dada pela expressão (5.11). \[ \begin{align} E(X)=\mu=\int_{-\infty}^{\infty} x f(x) \, dx. \end{align} \tag{5.11}\]

Exemplo 5.21 Para o Exemplo 5.16, e utilizando-se da expressão (5.11), tem-se:

\[\begin{align*} E(X) = \mu &=\int_{100}^{300} x \frac{x}{40.000}dx\\ &= \frac{1}{40.000}\int_{100}^{300} x^2dx\\ &= \left. \frac{1}{40.000}\frac{x^3}{3} \right|_{100}^{300}\\ &=\frac{27.000.000-1.000.000}{120.000}\\ &= \frac{26.000.000}{120.000}\\ &= 216,67~\textrm{horas}. \end{align*}\]

5.14.1.3 Propriedades

Se \(k\) é um valor constante e \(X\) uma variável aleatória, a esperança matemática apresenta as seguintes propriedades:

\(E(k) = k\);
\(E(X\pm k) =E(X)\pm k\);
\(E(kX) = kE(X)\);
\(E(X_1 + X_2 + \cdots + X_n) = E(X_1) + E(X_2) + \cdots + E(X_n)\), sendo \(X_1, X_2, \cdots, X_n\) variáveis aleatórias independentes.

5.14.2 Variância

A dispersão dos valores relativos a média é a variância da distribuição, denotado por \(V(X)\) ou \(\sigma^2\), sendo que discreta ou contínua, é definida pela expressão (5.12). \[ \begin{align} V(X)=\sigma^2=E[X-E(X)]^2=E(X^2) - [E(X)]^2. \end{align} \tag{5.12}\]

5.14.2.1 Variável Aleatória Discreta

No caso de variáveis aleatórias discretas, a \(E(X^2)\) e dada pela expressão (5.13). \[ \begin{align} E(X^2)=\sum_{i=1}^{\infty} x_i^2 P(X = x_i). \end{align} \tag{5.13}\]

Exemplo 5.23 Para o Exemplo 5.17, e utilizando-se da expressão (5.13) para o cálculo de \(E(X^2)\), tem-se: \[\begin{align*} E(X^2) & =0^2 \times (0,32) + 1^2 \times (0,28) + 2^2 \times (0,20) +\\ & \quad + 3^2 \times (0,12) + 4^2\times (0,06) + 5^2\times (0,02)\\ & = 3,62~(\textrm{lesões})^2 \end{align*}\]

Logo, utilizando-se da expressão (5.12), tem-se que a variância é dada por:

\[ V(X)=\sigma^2=3,62 - (1,38)^2=1,7156~(\textrm{lesões})^2. \] O desvio padrão é dado por: \[ \sigma=\sqrt{1,7156}=1,3098~\textrm{lesões}. \]

5.14.2.2 Variável Aleatória Contínua

No caso de variáveis aleatórias contínuas, a \(E(X^2)\) é dada pela expressão (5.14). \[ \begin{align} E(X^2)=\int_{-\infty}^{\infty} x^2 f(x) \, dx. \end{align} \tag{5.14}\]

Exemplo 5.22 Para o Exemplo 5.16, e utilizando-se da expressão (5.14) para o cálculo de \(E(X^2)\), tem-se: \[\begin{align*} E(X^2) & =\int_{100}^{300} x^2 \times \frac{x}{40.000}dx\\ & =\frac{1}{40.000}\int_{100}^{300} x^3 \, dx\\ & = \left. \left(\frac{1}{40.000}\frac{x^4}{4} \right)\right|_{100}^{300} =\frac{8.100.000.000-100.000.000}{160.000}\\ & = \frac{8.000.000.000}{160.000}\\ & = 50.000~(\textrm{horas})^2. \end{align*}\]

Logo, utilizando-se da expressão (5.12), tem-se que a variância é dada por:

\[ V(X)=\sigma^2=50.000 - (216,67)^2=3.054,11~(\textrm{horas})^2. \]

O desvio padrão é dado por:

\[ \sigma=\sqrt{3.054,11}=55,2640~\textrm{horas}. \]

5.14.2.3 Propriedades

Considerando X e Y duas variáveis aleatórias independentes e k uma constante, a variância apresenta as seguintes propriedades:

\(V(k) = 0\);
\(V(X \pm k) = V(X)\);
\(V(kX) = k^2V(X)\);
\(V(X \pm Y) = V(X) + V(Y)\).

Exercícios propostos

Exercício 5.1 Determine o espaço amostral para cada um dos experimentos abaixo:

Semear três sementes de uma variedade de milho e contar o número de sementes que germinam;
Em uma granja ovos são produzidos. Contar o número de ovos danificados em um período de vinte e quatro horas;
Moirões de Eucalipto para cercas de uma propriedade rural são construídos. Determinar o tempo de vida dos moirões até apodrecer.

Exercício 5.2 Para os experimentos do exercício anterior determine os seguintes eventos:

A: Exatamente duas sementes germinam; B: Pelo menos duas sementes germinam; C: No máximo uma semente germina.
A: Todos os ovos são perfeitos.
A: Os moirões dure no máximo cinco anos.

Exercício 5.3 A probabilidade de uma variedade A de café ser altamente produtiva daqui a cinco anos é de 0,90, e de uma outra variedade B é de 0,85. Determinar a probabilidade de que daqui a cinco anos:

Ambas as variedades sejam produtivas;
Somente a variedade A seja produtiva;
Somente a variedade B seja produtiva;
Nenhuma seja produtiva;
Pelo menos uma seja produtiva.

Exercício 5.4 Dois arados de disco A e B são colocados em teste por 1.000 horas. A probabilidade de que uma falha aconteça no arado A é de: \(\frac{1}{30}\), no arado B é de: \(\frac{1}{80}\), e em ambos de: \(\frac{1}{1.000}\). Qual a probabilidade de que:

Pelo menos um dos arados tenha apresentado falha;
Nenhum dos arados tenha apresentado falha;
Apenas o arado A tenha apresentado falha;
\(P(A | B)\);
\(P(B | A)\).

Exercício 5.5 Um Engenheiro Agrônomo conduziu uma pesquisa, com o objetivo de verificar se o grau de ataque de uma certa espécie de inseto em plantas de feijão, está relacionada com a deficiência de um certo nutriente que ocorre nas plantas. Assim considere o evento B que representa o conjunto das plantas que apresentam os sintomas de deficiência, e os eventos \(A_1\), \(A_2\), \(A_3\), referentes aos graus de desfolhamento causado pelo inseto, dados por:

\(A_1\): Alto;
\(A_2\): Moderado;
\(A_3\): Baixo.

Sejam também as seguintes probabilidades:

\(P(A_{1})=0,20\);
\(P(A_{2})=0,30\);
\(P(A_{3})=0,50\);
\(P(B | A_{1})=0,05\);
\(P(B | A_{2})=0,02\);
\(P(B | A_{3})=0,01\).

Dado que ocorre a deficiência do nutriente em uma planta, qual a probabilidade de que ela apresente um alto grau de desfolhamento.

Exercício 5.6 Classifique as seguintes variáveis aleatórias como discretas ou contínuas:

X: Produção de leite de vacas holandesas;
Y: Número de ovos danificados em um lote de uma granja;
Z: Número de frutos atacados por uma praga num pé de laranja;
M: Peso de leitões da raça Duroc aos 21 dias de idade;
N: Número de ovos depositados por um inseto nas folhas de pés de café;
O: Produção de milho numa área de 15 hectares.

Exercício 5.7 Seja uma variedade de feijão em que o poder de germinação é de 90,0%. Três sementes desta variedade são semeadas por cova. Seja a variável aleatória X: número de sementes que germinam. Determine:

O espaço amostral;
A distribuição de probabilidades da variável aleatória X;
A média e a variância da variável aleatória X;
A função de distribuição de probabilidade acumulada da variável aleatória X.

Exercício 5.8 Dada a seguinte distribuição de probabilidades da variável aleatória discreta X: número de ovos danificados em um lote.

\(\mathbf{x}\)	0	1	2	3	4	5
\(\mathbf{P(X = x)}\)	0	\(p^2\)	\(p^2\)	\(p\)	\(p\)	\(p^2\)

Ache o valor de \(p\);
Calcule: \(P(X \geq 4), P(X < 3) e P(X = 3)\);
Calcule a média e a variância de X;
Construa a função de distribuição de probabilidade acumulada.

Exercício 5.9 A probabilidade de um bovino ser resistente a um certo tipo de vírus da febre aftosa é de \(\frac{2}{3}\). Num lote de quatro bovinos considerando Y como sendo a variável aleatória que representa o número de animais susceptíveis ao vírus, pede-se:

O espaço amostral;
A distribuição de probabilidades de Y;
As seguintes probabilidades: \(P(Y \leq 2)\), \(P(1 < Y \leq 3)\) e \(P(Y > 1)\);
A média e a variância de Y;
A função de distribuição de probabilidade acumulada de Y.

Exercício 5.10 Seja \(f(x)\) a função densidade de probabilidade da variável aleatória contínua X: Tempo de vida produtiva de uma cultura perene, em anos, definida por: \[\begin{align*} f(x)=\begin{cases} \frac{2}{27}(x+1) & \textrm{para }2 < x < 5;\\ 0,0 & \textrm{caso contrário.} \end{cases} \end{align*}\]

Mostre que \(f(x)\) é uma função densidade de probabilidade legítima;
Calcule: \(P(X < 4); P(3 \leq X \leq 4)\);
Calcule a média e a variância de X;
Construa a função de distribuição de probabilidade acumulada de X.

Exercício 5.11 Suponha que o peso de frangos de corte de uma certa raça, em kg, pode ser descrito pela seguinte função densidade de probabilidade: \[\begin{align*} f(x)=\begin{cases} \frac{1}{6}x+\frac{1}{12} & \textrm{para }0 < x < 3;\\ 0,0 & \textrm{caso contrário.} \end{cases} \end{align*}\]

Calcule as seguintes probabilidades: \(P(X > 1,5); P(1,6 < X < 2,2); P(X < 2,3)\);
Qual a probabilidade de um frango pesar exatamente 1,8 kg;
Construa a função de distribuição de probabilidade acumulada;
Calcule a média e a variância.