4 Medidas de Dispersão – Estatística Básica aplicada às Ciências Agrárias

4.1 Introdução

O resumo de um conjunto de dados através de uma medida de posição, como por exemplo, a média, não revela toda a informação sobre a dispersão desse conjunto de dados. Por exemplo, considere o Exemplo 4.1.

Exemplo 4.1 Sejam três amostras referentes às alturas, em cm, de três variedades de milho, dadas por:

Variedade A: 185,0; 185,0; 185,0;
Variedade B: 182,0; 184,0; 189,0;
Variedade C: 176,0; 180,0; 199,0.

Utilizando-se da expressão (3.6) tem-se que a média para as três variedades são dadas por:

Variedade A:

\[ \bar{\text{x}}=\frac{185,0+185,0+185,0}{3}=185,0~\textrm{cm}. \]

Variedade B:

\[ \bar{\text{x}}=\frac{182,0+184,0+189,0}{3}=185,0~\textrm{cm}. \]

Variedade C: \[ \bar{\text{x}}=\frac{176,0+180,0+199,0}{3}=185,0~\textrm{cm}. \]

Baseando-se apenas na média as três variedades são consideradas como de mesma altura.

As medidas de posição são de tendência central e não informam sobre a variabilidade dos dados. Assim, faz-se necessário a utilização de uma medida que sumarizem a variabilidade de um conjunto de dados, e que permita, por exemplo, comparar diferentes conjuntos de dados baseando-se em algum critério.

As medidas de dispersão, também conhecida como medidas de variabilidade, são medidas que indicam o grau de afastamento de um conjunto de dados ao redor de um valor central, e são necessárias para junto com a média, representar bem um conjunto de dados.

4.2 Amplitude Total

Uma das formas mais simples de se medir a dispersão (variabilidade) de um conjunto de dados, é através da amplitude total. Define-se amplitude total como sendo a diferença entre o maior e o menor valor observado de um conjunto de dados dada pela expressão (4.1). \[ A=\textrm{Maior dado} - \textrm{Menor dado}. \tag{4.1}\]

Para dados agrupados em uma tabela de distribuição de frequências com intervalos de classes, a amplitude total é a diferença entre os pontos médios da última $(\tilde{X}_K)$ e da primeira classe $(\tilde{X}_1)$, dada pela expressão (4.2). \[ A=\tilde{X}_{K}-\tilde{X}_{1}. \tag{4.2}\]

Exemplo 4.2 Para o Exemplo 4.1 e utilizando-se da expressão (4.1) tem-se:

Variedade A:

\[ A=185,0-185,0=0,0~cm. \]

Variedade B:

\[ A=189,0-182,0=7,0~\textrm{cm}. \]

Variedade C:

\[ A=199,0-176,0=23,0~\textrm{cm}. \]

Exemplo 4.3 Considerando o Exemplo 2.4 e utilizando-se da expressão (4.1) tem-se:

\[ A=33,0-21,0=12,0~\textrm{kg}. \]

Apesar de ser uma medida fácil de ser calculada, a amplitude total não é muito usada para expressar a variabilidade de um conjunto de dados, pois baseia-se em apenas em dois dados, não considerando a totalidade dos dados do conjunto. Assim, faz-se necessário a apresentação de outras medidas que possam expressar a variabilidade de um conjunto de dados, que reflitam as diferenças de todos os dados do conjunto.

4.3 Variância e Desvio Padrão

Outra medida de dispersão amplamente usada para medir a variabilidade de um conjunto de dados é a variância. A variância mede a dispersão de um conjunto de dados em relação à sua média, e indica, o quanto em média, os dados se desviam em relação à média.

A variância permite, também, comparar a variabilidade entre conjuntos de dados que possuam a mesma média e a mesma unidade. Quanto menor for a variância, menos variável é o conjunto de dados.

4.3.1 Dados Não Agrupados

No caso de uma população, a variância é definida pela razão entre a soma de quadrados dos desvios de cada dado em relação à sua média, e o número total de dados, dada pela expressão (4.3). \[ \begin{align} \sigma^2=\frac{\sum_{i=1}^{N}\left(x_i-\mu\right)^2}{N}. \end{align} \tag{4.3}\] E no caso de uma amostra, a variância é dada pela expressão (4.4). \[ \begin{align} s^2=\frac{\sum_{i=1}^{n}\left(x_i- \bar{\text{x}} \right)^2}{n-1}. \end{align} \tag{4.4}\]

Desenvolvendo a soma de quadrados de (4.4), pode-se reescrever $s^2$ através da expressão (4.5). \[ \begin{align} s^2=\frac{\sum_{i=1}^{n}x_i^2-\frac{\left(\sum_{i=1}^{n}x_i\right)^2}{n}}{n-1}. \end{align} \tag{4.5}\]

A variância é expressa na unidade dos dados ao quadrado .

Exemplo 4.4 Considerando o Exemplo 4.1 e utilizando-se da expressão (4.4), tem-se:

Variedade A: \[\begin{align*} s^2 & = \frac{\left(185,0-185,0\right)^2+\left(185,0-185,0\right)^2+\left(185,0-185,0\right)^2}{3-1}\\ & = \frac{\left(0,0\right)^2+\left(0,0\right)^2+\left(0,0\right)^2}{2}\\ & = 0,0~\textrm{cm}^2. \end{align*}\]

Que também pode ser calculada por (4.5): \[\begin{align*} s^2 & =\frac{185,0^2+185,0^2+185,0^2-\frac{\left(185,0+185,0+185,0\right)^2}{3}}{3-1}\\ & = \frac{102.675,0-102.675,0}{2}\\ & = 0,0~\textrm{cm}^2. \end{align*}\]

Variedade B: \[\begin{align*} s^2 & = \frac{\left(182,0-185,0\right)^2+\left(184,0-185,0\right)^2+\left(189,0-185,0\right)^2}{3-1}\\ & = \frac{\left(-3,0\right)^2+\left(-1,0\right)^2+\left(4,0\right)^2}{2}\\ & = 13,0~\textrm{cm}^2. \end{align*}\] Que também pode ser calculada por (4.5): \[\begin{align*} s^2 & = \frac{182,0^2+184,0^2+189,0^2-\frac{\left(182,0+184,0+189,0\right)^2}{3}}{3-1}\\ & = \frac{102.701,0-102.675,0}{2}\\ & = 13,0~\textrm{cm}^2. \end{align*}\]
Variedade C: \[\begin{align*} s^2 & = \frac{\left(176,0-185,0\right)^2+\left(180,0-185,0\right)^2+\left(199,0-185,0\right)^2}{3-1}\\ & = \frac{\left(-9,0\right)^2+\left(-5,0\right)^2+\left(14,0\right)^2}{2}\\ & = 151,0~\textrm{cm}^2. \end{align*}\] Que também pode ser calculada por (4.5): \[\begin{align*} s^2 & = \frac{176,0^2+180,0^2+199,0^2-\frac{\left(176,0+180,0+199,0\right)^2}{3}}{3-1}\\ & = \frac{102.977,0-102.675,0}{2}\\ & = 151,0~\textrm{cm}^2. \end{align*}\]

Observa-se que a variedade C tem variância maior que as variedades A e B, indicando que seus dados dispersam mais em torno da média.

Exemplo 4.5 Considerando os dados do Exemplo 2.4 e utilizando-se da expressão (4.5), tem-se: \[\begin{align*} s^2 & = \frac{21,0^2+21,6^2+\cdots+31,8^2+33,0^2-\frac{\left(21,0+21,6+\cdots+31,8+33,0\right)^2}{50}}{50-1}\\ & = \frac{35.745,1-\frac{\left(1.330,2\right)^2}{50}}{49}\\ & = 7,2747~\textrm{kg}^2. \end{align*}\]

Sendo a variância uma medida expressa na unidade dos dados ao quadrado, isto pode trazer problemas do ponto de vista de interpretação. Logo, faz-se necessário o uso de uma outra medida que retorne os dados para sua unidade original. Assim, tem-se o desvio padrão que é a raiz quadrada positiva da variância.

No caso de uma população, o desvio padrão é dado por (4.6). \[ \begin{align} \sigma=\sqrt{\sigma^2}. \end{align} \tag{4.6}\]

E no caso de uma amostra, o desvio padrão é dado por (4.7). \[ \begin{align} s=\sqrt{s^2}. \end{align} \tag{4.7}\]

O desvio padrão, indica, em média, qual será o erro (desvio) cometido ao tentar substituir cada dado pela média.

Exemplo 4.6 No Exemplo 4.1 e utilizando-se de (4.7) , tem-se:

Variedade A: \[ s=\sqrt{0,0}=0,0~\textrm{cm}. \]
Variedade B:

\[ s=\sqrt{13,0}=3,6~\textrm{cm}. \]

Variedade C:

\[ s=\sqrt{151,0}=12,3~\textrm{cm}. \]

Exemplo 4.7

Considerando os dados do Exemplo 2.4 e utilizando-se da expressão (4.7), tem-se:

4.3.2 Dados Agrupados

Se os dados estiverem agrupados em uma Tabela de Distribuição de Frequências com intervalos de classes, a variância é dada pela expressão (4.8). \[ \begin{align} s^2=\frac{\sum_{i=1}^{k}F_{i}\tilde{X}_{i}^{2}-\frac{\left(\sum_{i=1}^{K}F_{i}\tilde{X}_{i}\right)^2}{\sum_{i=1}^{k}F_i}}{\left(\sum_{i=1}^{K}F_i\right)-1}, \end{align} \tag{4.8}\] em que: $\tilde{X}_i$ é o ponto médio da classe $i$, e $F_i$ é a frequência absoluta da classe $i$.

Exemplo 4.8 Considerando os dados do Exemplo 2.4. Alternativamente pode-se acrescentar mais duas colunas na tabela de distribuição de frequências referentes a: $F_{i}\tilde{X}_i$ e $F_{i}\tilde{X}_{i}^{2}$, apresentada na Tabela 4.1.

Tabela 4.1: Pesos ao nascer, em kg, de 50 bezerros da raça nelore, Fazenda XX, 2007.¹

Peso $\mathbf{(kg)}$	$\mathbf{\tilde{X}_i}$	$\mathbf{F_i}$	$\mathbf{Fr_i}$	$\mathbf{Fp_i(\%)}$	$\mathbf{F_{i}\tilde{X}_i}$	$\mathbf{F_{i}\tilde{X}_{i}^{2}}$
$\left[20,0 \right. ;\left. 22,0 \right)$	21,0	2	0,04	4,0	42,0	882,0
$\left[22,0 \right. ;\left. 24,0 \right)$	23,0	5	0,10	10,0	115,0	2.645,0
$\left[24,0 \right. ;\left. 26,0 \right)$	25,0	12	0,24	24,0	300,0	7.500,0
$\left[26,0 \right. ;\left. 28,0 \right)$	27,0	16	0,32	32,0	432,0	11.664,0
$\left[28,0 \right. ;\left. 30,0 \right)$	29,0	10	0,20	20,0	290,0	8.410,0
$\left[30,0 \right. ;\left. 32,0 \right)$	31,0	4	0,08	8,0	124,0	3.844,0
$\left[32,0 \right. ;\left. 34,0 \right)$	33,0	1	0,02	2,0	33,0	1.089,0
Total	-	50	1,00	100,0	1.336,0	36.034,0

Utilizando-se da expressão (4.8), tem-se que a variância é dada por: \[\begin{align*} s^2 &= \frac{36.034,0-\frac{\left(1.336,2\right)^2}{50}}{50-1}\\ &= 6,86~\textrm{kg}^2. \end{align*}\]

Consequentemente, o desvio padrão calculado através de (4.7) é dado por:

\[ s=\sqrt{6,86}=2,62~\textrm{kg}. \]

A diferença entre os dois valores (2,6972 kg e 2,62 kg) se deve ao erro de agrupamento.

4.3.3 Propriedades

A variância e o desvio padrão apresentam as seguintes propriedades.

Somando-se ou subtraindo-se um mesmo valor constante $k$ a cada dado, a variância e o desvio padrão não se alteram.

Exemplo 4.9 Considere o Exemplo 3.3, em que a variância foi calculada através de (4.5), e o desvio padrão por (4.7), e são dados por: $s^2=13,0~\textrm{cm}^2$ e $s=3,6~\textrm{cm}$.

Somando $k = 4$ a cada dado, tem-se: \[ 186,0; 188,0; 193,0. \]

Calculando a nova variância através de (4.5), tem-se: \[\begin{align*} s^2 &= \frac{186,0^2+188,0^2+193,0^2-\frac{\left(186,0+188,0+193,0\right)^2}{3}}{3-1}\\ &=\frac{107.189,0-107.163,0}{2}\\ &= 13,0~\textrm{cm}^2 \end{align*}\]

Calculando o novo desvio padrão por (4.7), tem-se: \[ s=\sqrt{13,0}=3,6~\textrm{cm}. \]

Como se observa, a variância e o desvio padrão não se alteraram.

Multiplicando-se ou dividindo-se cada dado por uma mesmo valor constante $k$, diferente de zero, a variância fica multiplicada ou dividida por este valor ao quadrado $(k^2)$, e o desvio padrão fica multiplicado ou dividido por este valor $(k)$.

Exemplo 4.10 Considere o Exemplo 3.3, em que a variância foi calculado através de (4.5), e o desvio padrão por (4.7), e são dados por: $s^2=13,0~\textrm{cm}^2$ e $s=3,6~\textrm{cm}$.

Multiplicando todos os dados por $k = 2$, tem-se: \[ 364,0; 368,0; 378,0. \]

Calculando a nova variância através de (4.5), tem-se: \[\begin{align*} s^2 &= \frac{364,0^2+368,0^2+378,0^2-\frac{\left(364,0+368,0+378,0\right)^2}{3}}{3-1}\\ &= \frac{410.804,0-410.700,0}{2}\\ &= 52,0~\textrm{cm}^2 \end{align*}\]

Calculando o novo desvio padrão por (4.7), tem-se:

\[ s=\sqrt{52,0}=7,2~\textrm{cm}. \]

Logo, tem-se que:

\[ s^2=(2)^2 \times 13,0=52,0~\textrm{cm}^2$ e $s=(2) \times 3,6=7,2~\textrm{cm}. \]

4.4 Coeficiente de Variação

O coeficiente de variação é uma medida de dispersão relativa, que expressa o desvio padrão em termos da média de forma percentual.

No caso de uma população, o coeficiente de variação é dado por (4.9). \[ \begin{align} CV=\frac{\sigma}{\mu} \times 100, \end{align} \tag{4.9}\] sendo: $\mu$ e $\sigma$, a média e o desvio padrão populacional, respectivamente.

Considerando uma amostra, o coeficiente de variação é dado por (4.10). \[ \begin{align} cv=\frac{s}{\bar{\text{x}}} \times 100, \end{align} \tag{4.10}\] sendo: $\bar{x}$ e $s$, a média e o desvio padrão amostral, respectivamente.

O coeficiente de variação é usado para comparar a variabilidade de dois ou mais conjuntos de dados, que possuam diferentes unidades e/ou diferentes médias.

Exemplo 4.11 Para o Exemplo 2.4 e utilizando-se a expressão (4.10), tem-se:

\[ cv=\frac{2,6972}{26,6} \times 100=10,14\%. \]

Exemplo 4.12 Sejam as alturas, em cm, de plantas de duas variedades de soja (A e B), em que a média e o desvio padrão são: \[\begin{align*} \textrm{Variedade A}~\begin{cases} \bar{\text{x}}= 48,5~\textrm{cm};\\ s=4,9~\textrm{cm}. \end{cases} \end{align*}\]

\[\begin{align*} \textrm{Variedade B}~\begin{cases} \bar{\text{x}}=63,2~\textrm{cm};\\ s=5,3~\textrm{cm}. \end{cases} \end{align*}\]

Qual das duas variedades de soja tem uma maior variabilidade com relação à altura, A ou B?

Embora as unidades sejam as mesmas, tem-se que neste caso as médias das duas variedades com relação a altura são diferentes, e assim, compara-se pelo coeficiente de variação.

Assim, calculando o coeficiente de variação para as variedades A e B através de (4.10), tem-se:

Variedade A:

\[ cv=\frac{4,9}{48,5} \times 100=10,10\%. \] - Variedade B: \[ cv=\frac{5,3}{63,2} \times 100=8,39\%. \] Logo, a variedade A tem altura mais variável do que a variedade B, pois seu coeficiente de variação foi maior.

Exemplo 4.13 Considere uma amostra de 10 plantas de certa variedade de soja, onde se mediu a altura e a produção, dados por:

\[\begin{align*} \textrm{Altura}~\begin{cases} \bar{\text{x}} = 59,2~\textrm{cm};\\ s=6,1~\textrm{cm}. \end{cases} \end{align*}\]

\[\begin{align*} \textrm{Produção}~\begin{cases} \bar{\text{x}}=10,1~\textrm{g/vagem};\\ s=1,4~\textrm{g/vagem}. \end{cases} \end{align*}\]

Quem possui uma maior maior variabilidade, a altura ou a produção?

Neste caso tem-se que as unidades das variáveis são diferentes, e assim compara-se pelo coeficiente de variação.

Assim, calculando o coeficiente de variação para as variáveis através de (4.10), tem-se:

Altura:

\[ cv=\frac{6,1}{59,2} \times 100=10,30\%. \]

Produção:

\[ cv=\frac{1,4}{10,1}\times 100=13,86\%. \] Logo, a produção desta variedade de soja é mais variável do que a altura, pois seu coeficiente de variação foi maior.

4.5 Erro Padrão da Média

O erro padrão da média é uma medida de dispersão que dá uma ideia da precisão com que a média populacional $\mu$ foi estimada, sendo obtida pela expressão (4.11). \[ \begin{align} s(\bar{\text{x}})=\frac{s}{\sqrt{n}}, \end{align} \tag{4.11}\] em que: $s$ é o desvio padrão amostral, e $n$ o tamanho amostral.

Exemplo 4.14 Seja uma lavoura de milho, onde se avaliou uma amostra de 30 plantas, referentes a altura, em cm, encontrando os seguintes resultados:

\[\begin{align*} \textrm{Altura}~\begin{cases} \bar{\text{x}}=208,0~\textrm{cm};\\ s=12,0~\textrm{cm}. \end{cases} \end{align*}\]

O erro padrão da média calculado através de (4.11), é dado por:

\[ s(\bar{\text{x}})=\frac{12,0}{\sqrt{30}}=2,2~\textrm{cm}. \]

Este resultado quer dizer que a média populacional $\mu$ foi estimada com um erro de 2,2 cm.

Tem-se de modo geral que, quanto menor for o erro padrão mais precisa será a estimativa da média populacional $\mu$.

O erro padrão é diretamente proporcional ao desvio padrão da amostra, ou seja:

\[ \uparrow s \Rightarrow \uparrow s(\bar{\text{x}}); \]

\[\downarrow s \Rightarrow \downarrow s(\bar{\text{x}}). \]

O erro padrão é inversamente proporcional ao tamanho da amostra, isto é:

\[ \uparrow n \Rightarrow \downarrow s(\bar{\text{x}}); \]

\[ \downarrow n \Rightarrow \uparrow s(\bar{\text{x}}). \]

4.6 Medidas de Assimetria e de Curtose

Foi visto no Capítulo 2 que, a forma do polígono de frequências permite classificar a distribuição de frequências quanto a simetria. Viu-se também que as medidas de posição e dispersão, fornecem importantes informações sobre o comportamento de um conjunto de dados. É possível, ainda, fornecer algumas informações adicionais, de maneira a completar o diagnóstico de um conjunto de dados.

4.6.1 Coeficiente de Assimetria

As medidas de dispersão conseguem captar o desvio em torno de um valor central, mas não conseguem transmitir a ideia do formato deste desvio. Assim, surge o conceito de simetria, que é o comportamento de uma curva a ambos os lados de um eixo de simetria.

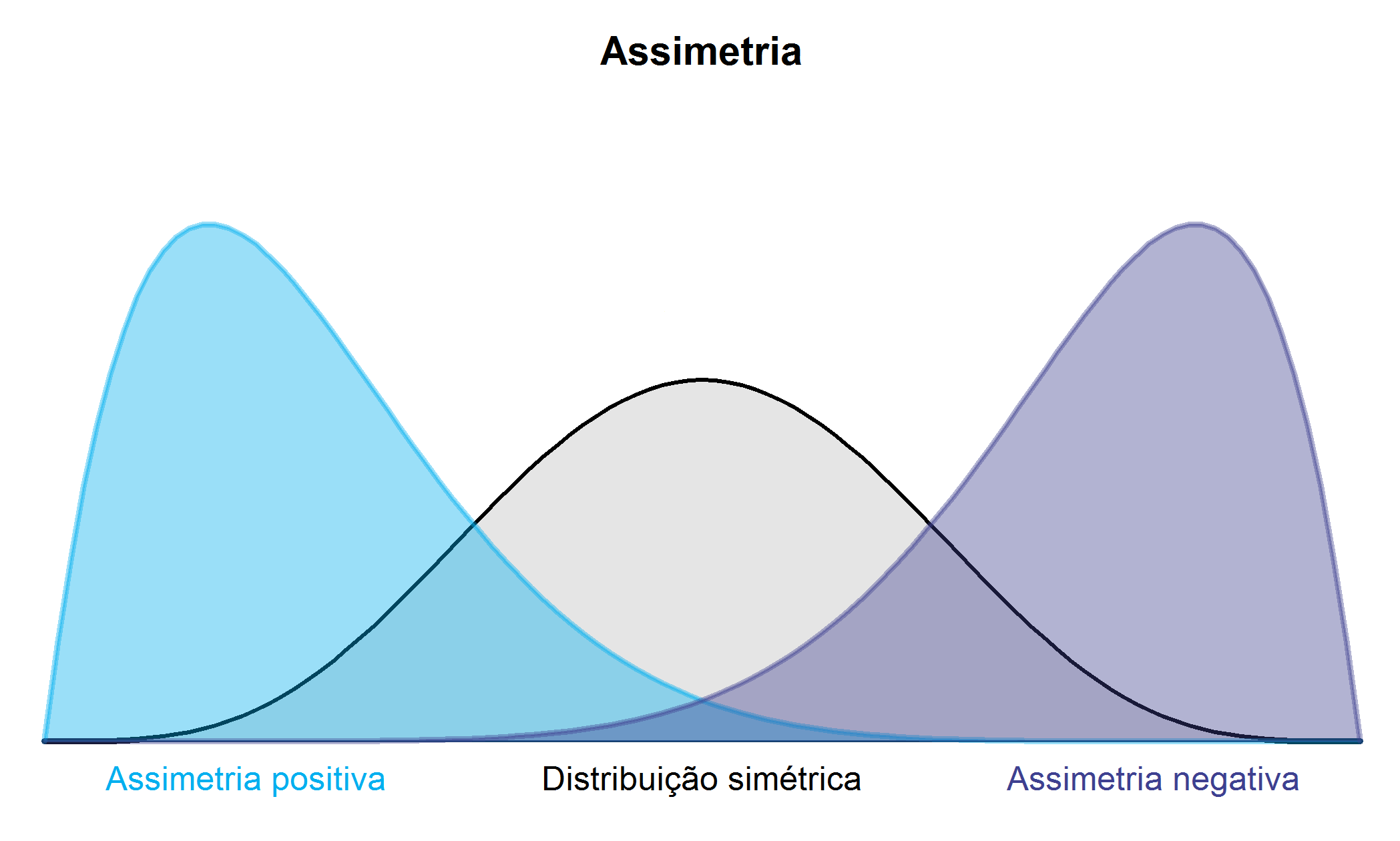
O coeficiente de assimetria mede o grau de desvio de uma curva no sentido horizontal, ou seja, quantifica o distanciamento de um conjunto de dados em relação à simetria, e é dado pela expressão (4.12). \[ \begin{align} a_3=\frac{\sum_{i=1}^{n}\left(x_i- \bar{\text{x}} \right)^3}{ns^3}. \end{align} \tag{4.12}\] O valor de $a_3$ pode ser:

Positivo: sendo a assimetria à direita (assimetria positiva), Figura 4.1;
Negativo: sendo a assimetria à esquerda (assimetria negativa), Figura 4.1;
Zero: apresentando uma simetria perfeita (distribuição simétrica), Figura 4.1.

Figura 4.1: Classificação da distribuição quanto a simetria.

Exemplo 4.15 Considere o Exemplo 2.4. Neste exemplo a média e o desvio padrão são: $26,6$ kg e $2,6972$ kg, respectivamente.

O coeficiente de assimetria calculado através de ( 4.12), é dado por: \[\begin{align*} a_3 &= \frac{(21,0-21,6)^3+(21,6-21,6)^3+\dots+(33,0-21,6)^3}{50(2,6972)^3}\\ &= \frac{126,5540}{981,0914}=0,1290. \end{align*}\]

Este valor indica uma leve assimetria à direita.

4.6.2 Coeficiente de Curtose

O conceito de curtose busca identificar se a curva que representa uma distribuição de frequências, apresenta uma forma achatada ou alongada.

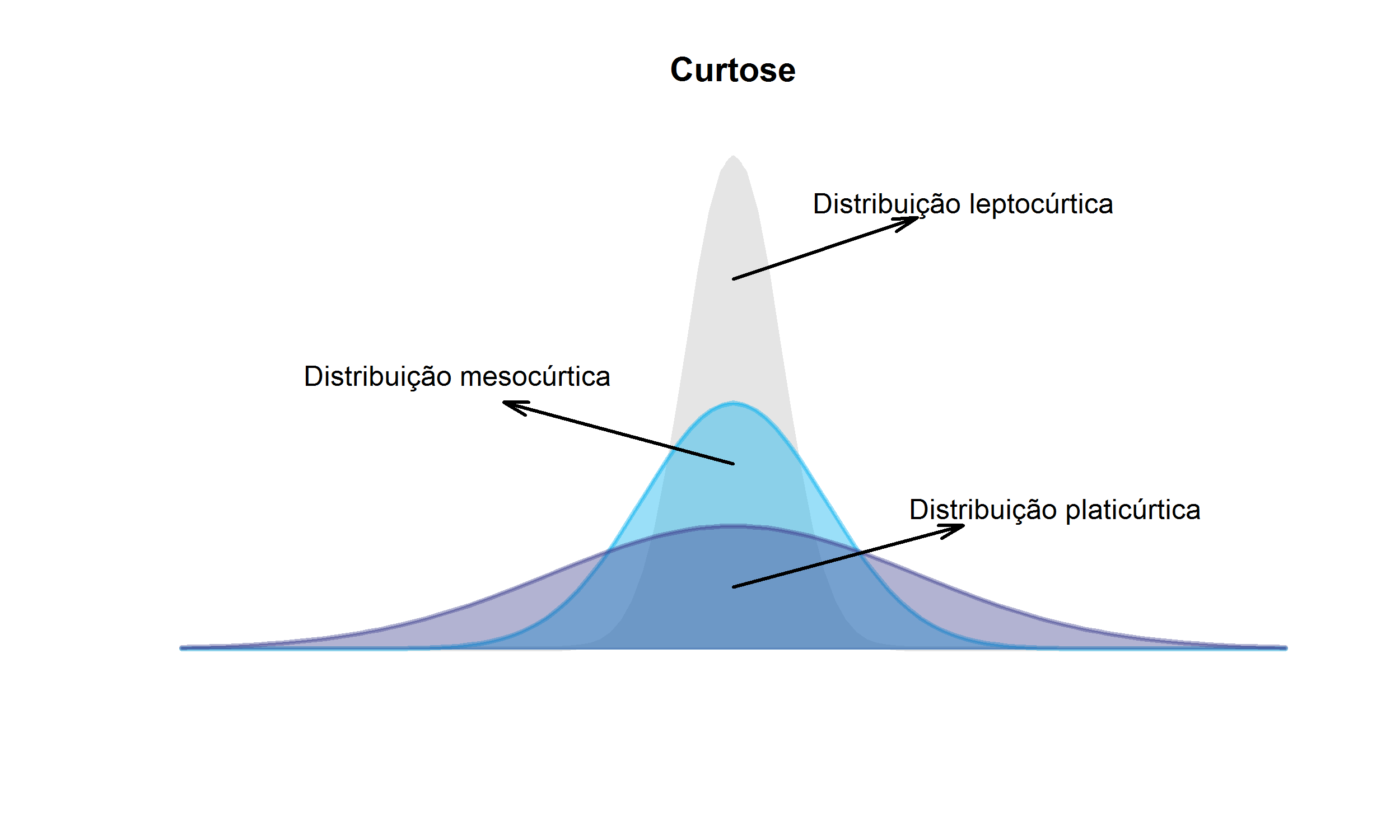
O coeficiente de curtose mede o grau de achatamento de uma curva, tendo a curva normal como referência, e é dado pela expressão (4.13). \[ \begin{align} a_4=\frac{\sum_{i=1}^{n}\left(x_i- \bar{\text{x}} \right)^4}{ns^4}. \end{align} \tag{4.13}\] O valor de $a_4$ pode ser:

Maior que 3: onde a curva apresenta um pico elevado, chamada de leptocúrtica, Figura 4.2.
Menor que 3: sendo a curva achatada, denominada de platicúrtica, Figura 4.2.
Igual a 3: apresentado uma curva intermediária, chamada de mesocúrtica, Figura 4.2.

Figura 4.2: Classificação da distribuição quanto a curtose.

Exemplo 4.16 Considere o Exemplo 2.4. A média e o desvio padrão são: 26,6~kg e 2,6972~kg, respectivamente.

Calculando o coeficiente de curtose através de (4.13), tem-se:

\[ a_4=\frac{(21,0-21,6)^4+(21,6-21,6)^4+\dots+(31,8-21,6)^4+(33,0-21,6)^4}{50(2,6972)^4} \]

\[ a_4=\frac{6.922,9210}{2.646,1997}=2,6162. \]

Indicando uma curva com um formato aproximadamente mesocúrtica.

4.7 Gráfico Box-Plots

As informações representadas pelo esquema dos cinco números, vistos no Capítulo 3, podem ser representadas graficamente num diagrama, chamado de Box-Plot. O Box-Plot é um gráfico que tem por objetivo apresentar várias informações sobre o comportamento de um conjunto de dados, tais como: posição, dispersão, simetria e dados discrepantes.

Neste tipo de gráfico considera-se um retângulo em que a mediana (2º Quartil), é representada pela parte central do retângulo, e os quartis inferior (1º Quartil) e superior (3º Quartil), pelas linhas à esquerda e à direita, que delimitam o retângulo, respectivamente, conforme a Figura 4.3. A posição da mediana, central ou mais próxima a um dos quartis, indica a presença ou não de assimetria nos dados.

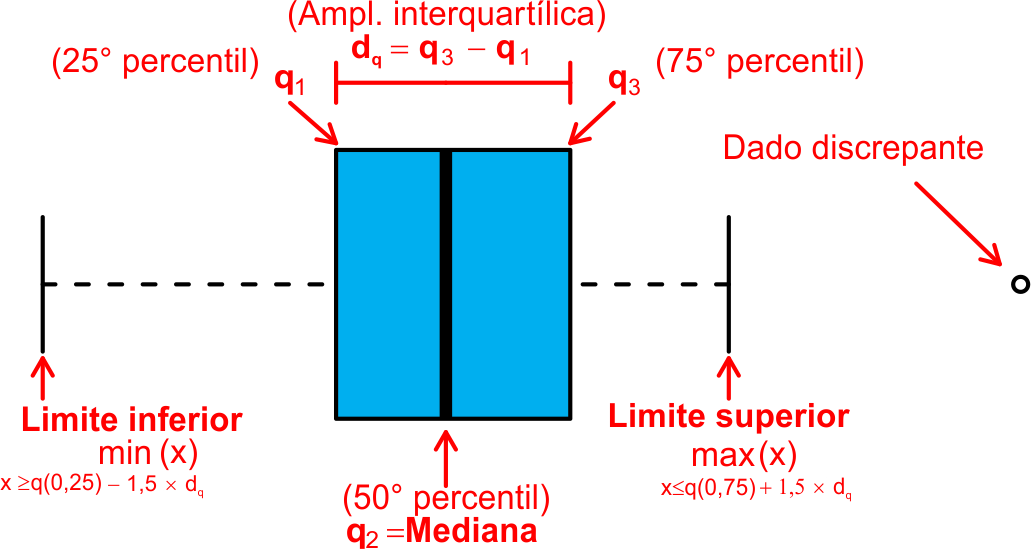
A dispersão dos dados é dada por (4.14). \[ \begin{align} d_q=q(0,75)–q(0,25). \end{align} \tag{4.14}\]

A partir do lado direito do retângulo, segue uma linha horizontal para a direita, que não exceda o limite superior, dado por (4.15). \[ \begin{align} LS=q(0,75)+(1,5)d_q. \end{align} \tag{4.15}\] E a partir do lado esquerdo do retângulo, segue uma linha horizontal para a esquerda, que não exceda o limite inferior, dado por (4.16). \[ \begin{align} LI=q(0,25)–(1,5)d_q. \end{align} \tag{4.16}\] Os valores que estiverem compreendidos entre esses dois limites, são chamados de valores adjacentes. As observações que estiverem fora desses limites (esquerda ou direita), serão chamadas de dados discrepantes, e representadas por um círculo (o).

Exemplo 4.17 Considerando o Exemplo 2.4, tem-se o seguinte gráfico Box-Plot apresentado na Figura 4.4.

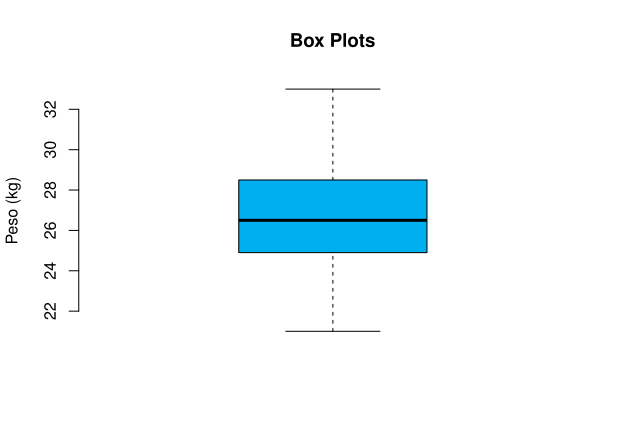
Figura 4.4: Gráfico de Box-Plot dos pesos ao nascer, em kg, de $50$ bezerros da raça nelore.

Observa-se pelo gráfico Box-Plot acima que, a distribuição é aproximadamente simétrica, e que a distribuição não apresenta valores discrepantes.

Uma outra característica é que este gráfico pode ser apresentado tanto na vertical quanto na horizontal.

Exercícios propostos

Exercício 4.1 Para comparar quatro variedades de alfafa (A, B, C, D), um Zootecnista conduziu um experimento em blocos casualizados com seis repetições. Os rendimentos de massa verde, em kg/parcela, foram os seguintes:

TRATAMENTOS/BLOCOS	1	2	3	4	5	6
A	56,8	57,2	57,5	55,4	56,0	57,9
B	53,5	54,3	53,8	54,7	53,3	52,6
C	54,0	53,5	52,8	54,2	53,6	54,1
D	54,5	54,5	54,5	54,5	54,5	54,5

Calcule a amplitude total para o tratamento A;
Calcule a variância para o tratamento D;
Qual tratamento é mais variável, o B ou o C? Justifique;
Calcule o desvio padrão para o tratamento A e interprete;
Multiplique os dados do tratamento A por 1.000,0 e calcule o desvio padrão;
Confronte os resultados de (d) com (e) e comente a diferença.

Exercício 4.2 Num concurso de produtividade de milho foram sorteadas seis parcelas de 40 $\textrm{m}^2$, em lavouras de dois produtores rurais de uma determinada região produtora de milho. Na colheita foram pesados os rendimentos das parcelas, em kg, fornecendo os seguintes resultados:

Produtor A	Produtor B
24,0	17,0
23,0	23,0
26,0	18,9
21,0	22,0
27,0	19,0
23,0	21,0

Qual foi o rendimento médio, em kg/parcela, e o erro padrão da média de cada produtor;
Qual produtor teve o rendimento médio estimado com maior precisão? Justifique;
Qual é a produtividade média do produtor A em t/ha;
Calcule a produtividade média, em t/ha, e o erro padrão da média para o produtor B;
Se a lavoura do produtor B tem 400 ha, qual será a sua produção total;
Quantas parcelas você recomendaria usar num próximo concurso, para estimar a produtividade média do produtor A com um erro padrão 30% menor.

Exercício 4.3 Tem-se abaixo informações climáticas mensais de uma determinada região produtora de arroz:

Medida	Média	Desvio padrão
Temperatura $(^{\circ}$C)	22,0	2,0
Precipitação $(\textrm{mm})$	100,0	15,5

Qual das medidas (temperatura ou precipitação) possui maior variabilidade. Justifique;
Uma vez registrados os dados descobriu-se que o instrumento utilizado para medir a precipitação estava aumentando sistematicamente 4 unidades (4~mm) em cada medição. Após corrigido o erro, qual atributo meteorológico é mais variável. Justifique.

Exercício 4.4 Para estudar a produtividade de um canavial um Engenheiro Agrônomo demarcou nele em vários pontos escolhidos ao acaso, 10 pequenas áreas de 100 $\textrm{m}^2$ cada, cuja produção foi pesada. Os resultados obtidos, em kg, foram os seguintes:

\[ 650,0; 850,0; 710,0; 920,0; 780,0; 820,0; 900,0; 780,0; 740,0; 950,0 \]

Calcule a variância, o desvio padrão, o coeficiente de variação e o erro padrão da média da produção de cana-de-açúcar por área de 100 $\textrm{m}^2$;
Você acha que a variabilidade dos dados em relação à sua média é grande ou pequena. Justifique.

Exercício 4.5 Em relação ao estudo do problema anterior, o Engenheiro Agrônomo achou que a variabilidade dos dados era muito grande, e que apenas 10 áreas de 100 $\textrm{m}^2$ não podiam representar bem a produtividade do canavial. Assim ele avaliou no lugar de 10, uma amostra de 50 áreas de 100 $\textrm{m}^2$, seguindo a mesma metodologia explicada no problema anterior. Os resultados obtidos, em kg, são apresentados na seguinte tabela de distribuição de frequências.

Tabela 4.2: Produção de cana-de-açúcar, em kg, por áreas de 100 $\textrm{m}^2$, Fazenda XX, 2007.²

Produção $\mathbf{(kg)}$	$\mathbf{\tilde{X}_i}$	$\mathbf{F_i}$
$\left[624,0 \right. ;\left. 668,0 \right)$	646,0	1
$\left[668,0 \right. ;\left. 712,0 \right)$	690,0	5
$\left[712,0 \right. ;\left. 756,0 \right)$	734,0	15
$\left[756,0 \right. ;\left. 800,0 \right)$	778,0	13
$\left[800,0 \right. ;\left. 844,0 \right)$	822,0	7
$\left[844,0 \right. ;\left. 888,0 \right)$	866,0	5
$\left[888,0 \right. ;\left. 932,0 \right)$	910,0	3
$\left[932,0 \right. ;\left. 976,0 \right)$	954,0	1
Total		50

Calcule a variância, o desvio padrão e o coeficiente de variação, da produção de cana-de-açúcar por área de 100 $\textrm{m}^2$;
Após registrada a produção de cada uma das 50 áreas de 100 $\textrm{m}^2$, o Engenheiro Agrônomo descobriu um erro sistemático na pesagem da cana-de-açúcar. Para obter a pesagem certa ele determinou que, em cada um dos 50 dados obtidos deveria ser acrescido 6,0 kg e depois o resultado deveria ser multiplicado por 0,9. Qual o valor correto da variância, do desvio padrão e do coeficiente de variação. O pesquisador conseguiu diminuir a variabilidade? Justifique.

Exercício 4.6 Os ganhos de peso, em kg, de 60 novilhos da raça guzerá, mantidos numa pastagem em determinado período foram os seguintes:

36,0	45,0	60,0	39,0	57,0	32,0	39,0	40,0	63,0	37,0
42,0	42,0	44,0	30,0	47,0	39,0	15,0	39,0	25,0	39,0
57,0	48,0	44,0	37,0	44,0	38,0	21,0	56,0	52,0	50,0
31,0	34,0	36,0	38,0	43,0	24,0	38,0	41,0	46,0	42,0
28,0	31,0	32,0	49,0	39,0	19,0	49,0	39,0	42,0	43,0
20,0	58,0	34,0	56,0	35,0	50,0	27,0	36,0	40,0	37,0

Calcule os coeficientes de assimetria e de curtose e discuta os resultados;
Construa o gráfico Box-Plot e interprete.